2545

1.9.3. Замкнутый контур

Для определения усилий в системе, содержащей замкнутый контур, необходимо расчленить его на образующие диски. При «раскрытии» контура сечения целесообразно проводить в местах соединения дисков единичными или шарнирными связями. При этом в местах сечений появятся соответственно одна или две неизвестные силы.

Пример . Построить эпюры M, Q, N в системах с замкнутым контуром (рис. 1.56,а).

Решение. Выполним кинематический анализ.

W 3D 2Ш Соп 3 3 2 3 3 0.

Необходимый признак геометрической неизменяемости выполняется. Структурный анализ показывает, что система состоит из трех дисков, соединенных тремя шарнирами C, D, B и не лежащих на одной прямой, и прикреплена к основанию тремя связями, непараллельными и не пересекающимися в одной точке, т.е. данная система кинетически неизменяема.

Опорные реакции определим из всей системы:M A 0.

4 5 RB 6 1 4 4 0;

Dx 83.

Стержень (диск) ВС.

M B 0.

Cx 3 Cy 4 q 4 2 0;

Cy 20 1 4 2 3 кН. 4

41

Рис. 1.56

42

На рис. 1.56,в показаны необходимые для построения эпюр внешние силы. Эпюры M , Q, N приведены на рис. 1.56,г,д,е.

Пример №2 (рис. 1.57).

Рис. 1.57

Самостоятельная работа. Построить эпюры M , Q, N для схем,

показанных на рис. 1.58.

43

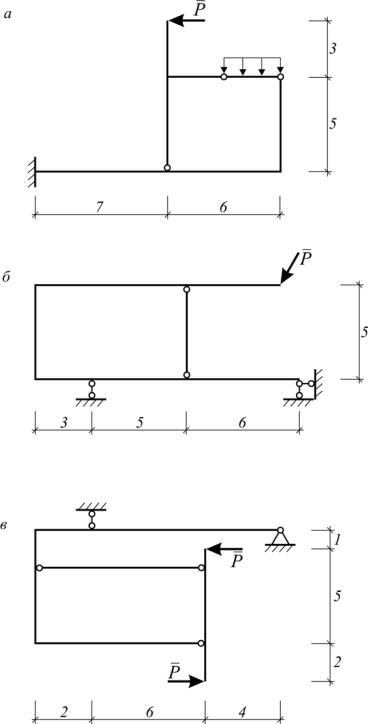
Рис. 1.58

44

2. РАСЧЕТ БАЛОК НА ПОДВИЖНУЮ НАГРУЗКУ. ЛИНИИ ВЛИЯНИЯ

2.1. Линии влияния

Эпюра внутренних сил (например изгибающих моментов) – это график усилий во всех сечениях всех элементов стержневой системы от какого-либо внешнего воздействия – внешней нагрузки, температуры. Если надо выяснить, как какое-либо одно определенное усилие в данном сечении (в данной точке) зависит от расположения внешней силы – строят линию влияния.

Рассмотрим изменение опорной реакции, поперечной силы и момента в сечении, когда по балке перемещается один вертикальный груз Р, равный единице. Установим закон изменения каждого из этих усилий в зависимости от положения перемещающегося груза Р=1.

График, отражающий изменение усилия в зависимости от положения единичного подвижного груза, называется линией влияния этого усилия.

В задачах на построение линий влияния положение груза Р=1 (абсцисса) будет независимой переменной, а изучаемое усилие (реакция данной опоры, момент в данном сечении, поперечная сила в данном сечении) будет искомой функцией.

Ордината линии влияния показывает величину данного усилия, когда груз Р=1 находится над этой ординатой.

1.Линии влияния опорных реакций.

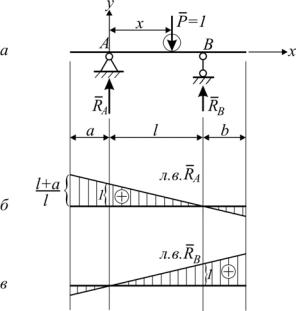
Начало координат поместим в точке А (рис.2.1,а). Поставив груз Р=1 в произвольное положение, находим выражение для левой опорной реакции RA в функции от х.

Рис. 2.1. Линии влияния реакций балки

45

Через две полученные точки проводим прямую – линию влияния

Линия влияния реакции RB показана на рис. 2.1,в.

2.Линия влияния поперечной силы в сечении.

Построим линию влияния поперечной силы в сечении I-I. Поперечная сила в сечении равна сумме проекций на нормаль к оси всех внешних сил, приложенных к отсеченной части балки. Поперечную силу считаем положительной, если равнодействующая левых сил направлена вверх от оси балки или равнодействующая правых сил – вниз от оси.

Рис. 2.2. Линии влияния поперечной силы в сечениях I-I, II-II, III-III

46

Разберем два положения груза на балке.

1)Груз справа. Рассмотрим равновесие левой части.

Всумму проекций войдет только левая реакция RA .

QI-I RA .

Знак линии влияния положительный.

2)Груз слева. Рассмотрим равновесие правой части.

Всумму проекций войдет только правая реакция RB .

Действительная часть линии влияния строится там, где был груз, т.е. слева от сечения. Линяя влияния QI-I изображена на рис. 2.2,б.

Построим линию влияния поперечной силы в сечении II-II. 1) Груз справа. Рассмотрим равновесие левой части.

QII-II 0.

л.в.QII-II 0.

Рис. 2.5

2) Груз слева. Рассмотрим равновесие левой части.

QII-II P 1.

л.в.QII-II 1.

Данная линяя влияния показана на рис. 2.2,в. Аналогичным образом строим линии влияния попе-

речной силы в сечении III-III (рис. 2.2,г). 3. Линия влияния момента в сечении.

Изгибающий момент в сечении равен сумме моментов внешних сил, приложенных к отсеченной части балки относительно точки сечения,

лежащей на оси. Момент левых сил примем положительным, если он действует по часовой стрелке, а момент правых сил – положительным, если он действует против часовой стрелки.

Линяя влияния момента в сечении I-I.

47

2.2. Определение усилий по линиям влияния

Ордината линий влияния показывает величину усилия, когда единичный груз находится над данной ординатой. Например, момент в сечении I-I

(см. рис. 2.7) равен нулю, когда груз находится над опорой В, и равен cbl ,

когда груз находится на краю правой консоли.

Если на балку действует сила F1 (рис. 2.10,а), то величина усилия, для которого построена линия влияния, равна:

S F1 y1.

Рис. 2.10

При действии на балку нескольких сил (рис. 2.11,а) в силу принципа суперпозиции

SI I F1 y1 F2 y2 Fn yn.

Для вычисления усилий от равномерно распределенной нагрузки (рис. 2.12,а) необходимо подсчитать площадь линии влияния под распределенной нагрузкой. Усилия в сечении I-I определяются по формуле

SI I q ,

где – площадь загруженного участка линии влияния.

При действии на балку неподвижного сосредоточенного момента (рис. 2.13,а) представим его в виде пары сил F и F с плечом а.

M F a .

Рис. 2.11

Рис. 2.12

49

Тогда усилие можно вычислить по уже известному правилу:

SI-I F y1 F y2 F( y2 y1)

Fa ( y2 y1) M tg . a

SPi yi qi i M K tg K .

2.3.Линии влияния в многопролетной балке

Линии влияния в многопролетных балках строятся с использованием поэтажной схемы. Вначале строится линяя влияния для простой балки, которой принадлежит рассматриваемое усилие. Затем линяя влияния распространяется на вышележащие на поэтажной схеме балки. Пример построения линий влияния для многопролетной балки приведен на рис.2.8. Для этого же примера произведено вычисление усилий от нагрузки по линиям влияния.

Вычислим усилия от нагрузки по линиям влияния по формуле

50