
2545
.pdf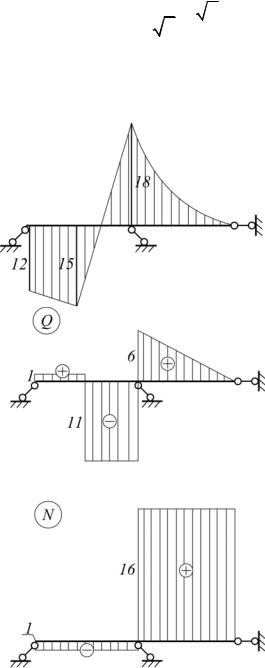
Определяем опорные реакции:
|
M K 0. |
12 1 6 6 RC 3 0; |
|||||
R |
48 16 кН. |
|
|
|
|
|
|
C |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M A 0. |
RB 0,707 6 12 3 6 9 12 0; |
||||||
R |
102 |
24,045 кН. |
|
|
|||
|
|
|
|||||
B |
4,242 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fky 0. |
RA 0,707 RB |
0,707 12 6 0; |
|||||
RA |
17 18 |
1 |
|
|
2 |
2 1,414. |
|
0,707 |
|
2 |
|||||
|
0,707 |
|
|
|
|||
Проверка: Fkx 0. RA 0,707 RB 0,707 16 1 17 16 0.
Строим эпюры (рис. 1.45).
М
Рис. 1.45. Эпюры M ,Q, N
31

Расчет статически определимых многопролетных балок (см., например, рис. 1.46,а) удобно выполнять в следующей последовательности:
Рис. 1.46
32

1.Строится поэтажная схема взаимодействия элементов многопролетной балки (рис. 1.46,б).
2.Последовательно определяются реакции и строятся эпюры внутренних усилий для отдельных балок начиная с верхней на поэтажной схеме (рис. 1.46,в,г,д,е,ж,и,к,л,м,н,о).
3.Строятся эпюры внутренних усилий для многопролетной балки
(рис. 1.46,п, р).
1.9.Трехшарнирные арки и рамы (распорные системы)
1.9.1. Основные понятия
Аркой называется несущая конструкция криволинейного или ломаного очертания, обращенная выпуклостью в сторону, противоположную действию нагрузки. В опорах арок от вертикальной нагрузки возникают наклонные реакции, направленные, как правило, внутрь пролета. Горизонтальная составляющая называется распором.
Трехшарнирная арка представляет собой статически определимую распорную систему, состоящую из двух полуарок, соединенных между собой и с поверхностью земли шарнирами.
Рис. 1.47
Опорные шарниры называют пятовыми, а средний – ключевым. Расстояние от линии, соединяющей опоры, до ключевого шарнира называют
стрелой подъема арки f.
Трехшарнирные арки и рамы могут иметь опоры на одном и на разных уровнях (рис.1.48).
В трехшарнирных арках одна из неподвижных опор может быть заменена на вертикальную подвижную опору. В этом случае для обеспечения геометрической неизменяемости вводится затяжка (рис.1.49), которая и воспринимает распор.
33
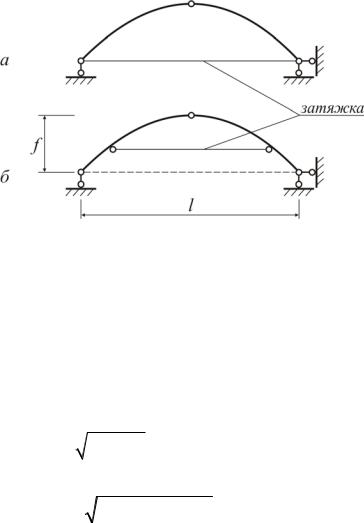
Рис. 1.49
Координаты оси арки y f (x) , угол наклона касательной к оси арки, а также sin и cos могут быть определены по следующим формулам:
а) ось арки – квадратная парабола: |
|
||
|
y 4 fx(l x) / l2 ; |
(1.6) |
|
|
tg y 4 f (l 2x) / l2 ; |
(1.7) |
|
cos |
1 |
; sin cos tg ; |
(1.8) |
1 tg2 |
|||
б) ось арки – часть окружности:
y |
R2 (l / 2 x)2 R f ; |
(1.9) |
|
R f / 2 l2 / 8 f ; |
(1.10) |
sin (l 2x) / 2R ; cos ( y R f ) / R . |
(1.11) |
|
Пример расчета трехшарнирной арки на неподвижную вертикальную нагрузку (рис. 1.50,а). Ось арки – квадратная парабола. Геометрия арки дана уравнениями (1.6)-(1.8).
Расчет арки производим в такой последовательности:
1) Вертикальные реакции определяем из уравнений моментов, относительно опор:
M A 0;
q1 24 12 P1 24 P2 36 q2 24 36 VB 48 0. VB 44 кН.
M B 0;
q1 24 36 P1 24 P2 12 q2 24 12 VA 48 0. VA 50 кН.
34

Рис. 1.50
35

Правильность вычисления вертикальных реакций проверяем с помощью уравнения
Fky VA q1 24 P1 P2 q2 24 VB50 48 10 12 24 44 94 94 0.
Балочные эпюры M 0 и Q0 показаны на рис. 1.51.
Рис. 1.51
2) Усилие в затяжке вычисляем по формуле
MC 0
для одной из рассеченных на две части по шарниру и затяжке частей арки. Например, для левой части (рис.1.52):
Mc лев 0;
VA 24 q1 24 12 H ( f t) 0.
36

Рис. 1.52
Откуда
H 50 24 2 24 12 6
Заметим – чем больше f, тем меньше величина распора H. Проверку Н делаем для другой отсеченной части арки:
Mc прав 0;
q2 24 12 P2 12 VB 24 H 6
1 24 12 12 12 44 24 104 6 1056 1056 0.
1.Арку разбиваем на восемь частей с горизонтальными проекциями, равными 6 м (рис. 1.50,б). Кроме того, крайние участки арки разбиваем точкой присоединения затяжки.
Расчетная схема арки показана на рис. 1.50,а.
Вычисляем координаты yi сечений, углы наклона оси арки i , а также
sin и cos .
2. Строим балочные эпюры M 0 ,Q0 для простой балки того же пролета
инагрузки (см. рис.1.51).
3.Составляем формулы для вычисления Mi ,Qi и Ni для арки.
Для участков выше затяжки: |
|
|
|
|
|||||
|
|
M x VA x Pk x ak H y t , |
(1.12) |
||||||
или |
|
M x |
M x0 |
H ( y t). |
|
(1.13) |
|||
|
|
Qx VA Pk cos H sin , |
(1.14) |
||||||
или |
|
Q Q0 cos H sin . |
|
||||||
|
|
(1.15) |
|||||||
|
|
|
|
x |
x |
|
|
|
|
|
|
Nx VA Pk sin H cos , |
(1.16) |
||||||
или |
|
|
|
Q0 |
|
|
|
|
|
|
|
N |
x |
sin H cos. |
(1.17) |
||||
|
|
|
|
x |
|
|
|
|
|
Для участков ниже затяжки: |
|
|
|
|
|
||||
M |
x |
M 0; |
Q Q0 |
cos; N |
x |
Q0 sin . |
(1.18) |
||
|
x |
|
|
x x |
|
x |
|
||
|
|
|
|
|
37 |
|
|
|
|
4. Окончательно заполняем таблицу.
№ |
Координаты |
0 |
sin |
cos |
M x0 |
M x |
Qx0 |
Qx |
Nx |
|
п/п |
x |
y |
|
|
|
|
|
|
|
|
0 |
0 |
0 |
33,69 |
0,555 |
0,833 |
0 |
0 |
50 |
41,7 |
-27,8 |
1 |
3,2 |
2,0 |
30,00 |
0,5 |
0,867 |
149,76 |
149,76 |
43,6 |
37,8 |
-21,8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-14,2 |
-112 |
2 |
6,0 |
3,5 |
26,57 |
0,446 |
0,895 |
264 |
108 |
38 |
-13,5 |
110,4 |
3 |
12,0 |
6,0 |
18,43 |
0,316 |
0,948 |
456 |
40 |
26 |
-8,3 |
-106,9 |
4 |
18,0 |
7,5 |
9,46 |
0,165 |
0,986 |
576 |
4 |
14 |
-3,4 |
-104,7 |
5 |
24,0 |
8,0 |
0 |
0 |
1 |
624 |
0 |
2 |
2 |
-104 |
|
|
|
|
|
|
|
|
-8 |
-8 |
|
|
-30,0 |
7,5 |
-9.46 |
-0,165 |
0,986 |
558 |
-14 |
-14 |
3,4 |
-104,7 |
7 |
36,0 |
6,0 |
-18,43 |
-0,316 |
0,948 |
456 |
40 |
-20 |
13,9 |
-105 |
|
|
|
|
|
|
|
|
-32 |
2,6 |
108,8 |
8 |
42,0 |
3,5 |
-26,57 |
-0,456 |
0,895 |
246 |
90 |
-38 |
13,5 |
-110,4 |
9 |
44,8 |
2,0 |
-30,00 |
-0,5 |
0,867 |
135,7 |
135,7 |
-40,8 |
16,6 |
-110,6 |
|
|
|
|
|
|
|
|
|
-35,4 |
-20,4 |
10 |
48,0 |
0 |
-33,69 |
-0,555 |
0,833 |
0 |
0 |
-44 |
-36,7 |
-24,4 |
По данным таблицы строим эпюры M x ,Qx и Nx для арки с затяжкой
(см. рис.1.50,в,г,д).
1.9.2. Расчет трехшарнирной рамы
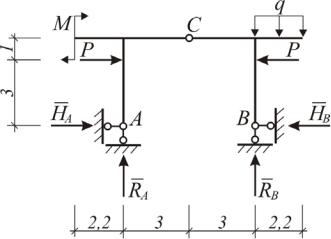
Построить эпюры M, Q, N для трехшарнирной рамы от заданной нагрузки. Схема рамы приведена на рис. 1.53,а. Исходные данные: p 28 кН;
М 48 кН м; q 12 кН/м.
Рис. 1.53
38

Решение. Расчет рамы начинаем с определения опорных реакций.
M B 0;
1.RA 6 P 3 P 3 M q 2,2 1,1 0;
RA M q 2,2 1,1 48 12 2,2 1,1 12,84 кН. 6 6
M A 0;
2.RB 6 P 3 P 3 q 2,2 7,1 M 0;
RA M q 2,2 7,1 48 12 2,2 7,1 39,24 кН. 6 6
Проверка:
Fxy 0;
RA RB q 2,2 12,84 39,24 12 2,2 39,24 39,24 0.
Определяем распор:
MC лев 0; |
|
|
|
|
|
|
RA 3 M P 1 H A 4 0. |
|
|
|
|
||
H A |
RA 3 M P 1 |
12,84 3 48 28 |
4,63 кН. |
|
||
|
4 |
|
|
4 |
|
|
MC прав 0; |
|
|
|
|
|
|
HB 4 P 1 q 2,2 4,1 RB 3 0. |
|
|
||||
HB |
P 1 q 2,2 4,1 RB 3 |
|
28 12 2,2 4,1 39,24 3 |
4,63 кН. |
||
4 |
|
|
4 |
|||
|
|
|
|
|
||
Проверка:
Fxy 0;
P P H A HB 28 28 4,63 4,63 0.
Определив реакции, построим эпюры М (рис.1.54,а), Q (рис.1.54,б),
N (рис. 1.54,в):
39

Рис. 1.54
Для построения эпюры N вырезаем два верхних узла рамы (рис. 1.55) и по эпюре Q из условий равновесия определяем продольные силы.
Рис. 1.55
40
