
2545
.pdf
Пример 1.3 (рис.1.28)
Рис.1.28. Кинематический анализ многопролетной балки
Условие то же, что и в примере 1.2. Количество дисков D=4; Количество шарниров Ш=3; Количество опорных связей C0 5;
W 3 4 2 3 5 1.
Действительно, балки АВ и DE (диски D1 и D4 ) являются в данной конструкции основными и геометрически неизменяемыми, а диски D2 и D3 представляют собой изменяемую часть конструкции, так как шарниры Ш1 , Ш2 и Ш3 лежат на одной прямой (рис. 1.28,в).
Пример 1.4 (рис. 1.29)
Рис.1.29. Кинематический анализ многопролетной балки
Условие то же, что и в примере 1.2.
Произвести проверку геометрической неизменяемости.
21

Количество дисков D=4; количество шарниров Ш=3; количество опорных связей C0 6 ;
W 3 4 2 3 6 0 ,
т.е. необходимое условие геометрической неизменяемости выполнено. Но рассматриваемая система изменяема (рис 1.29,б), т.к. в одном из второстепенных дисков (ВС, CDE или EF) недостает одной вертикальной связи, а одна горизонтальная связь, например в точке F – лишняя. Система может быть превращена в геометрически неизменяемую и статически определимую путем перестановки этой связи так, как это показано, например, на рис. 1.29,в.
Пример 1.5. Произвести проверку геометрической неизменяемости рамы (рис.1.30).
Количество дисков D=8; количество шарниров Ш=8;
количество опорных связей C0 8 (см. рис. 1.31а);
W 3 8 2 8 8 0 ,
т.е. необходимое условие геометрической неизменяемости выполнено.
Рис. 1.30. Расчетная схема рамы
Проведем структурный анализ.
Диски D4 , D5 , D6 образуют геометрически неизменяемый треугольник, т.к. соединены шарнирами, не лежащими на одной прямой. Диск D7
является основным, так как он связан с землей тремя связями. Шарнирный треугольник соединен с основным диском D7 в точке L с помощью шарни-
ра и с помощью единичной связи ( D8 ) с землей. Таким образом, указанная
22

система дисков представляет собой неизменяемую часть конструкции Dпр (рис. 1.30,б). Диск D1 также является основным (он однотипен с диском D7 ), а диск D3 можно считать одиночной связью.
Рис.1.31. Кинематический анализ рамы
Таким образом, прикрепление диска D2 к основному диску D1 производится с помощью шарнира и к неизменяемой части Dпр – с помощью одиночной связи D3 , также соединение обеспечивает его геометрическую
неизменяемость. Так как доказана геометрическая неизменяемость отдельных частей системы, то и вся система является геометрически неизменяемой.
Пример 1.6 (рис. 1.32а).
Рис. 1.32. Кинематический анализ рамы
Условие то же, что и в примере 1.5.
Произвести проверку геометрической неизменяемости. Количество дисков D=4;
количество шарниров Ш=4;
23

количество опорных связей C0 4 ;
W 3 4 2 4 4 0 .
Т.e. необходимое условие геометрической неизменяемости выполняется. Проведем анализ схемы образования системы.
Диски D3 и D4 (рис. 1.32,б) можно рассматривать как одиночные связи между дисками D1 и D2 . В качестве одиночной связи между дисками D1 и D2 можно рассматривать и диск основания. Тогда получается, что диски D1 и D2 соединены тремя одиночными связями. При этом диск основания
не параллелен связям EF и CD. Следовательно, диски соединены тремя связями в неизменяемую систему.
Пример 1.7 (рис. 1.33,а). Произвести проверку геометрической неизменяемости плоской фермы.
Рис.1.33. Проверка геометрической неизменяемости плоской фермы
Для подсчета количества дисков и количества шарниров рассмотрим ферму отдельно от связей (рис. 1.33,б).
Количество дисков D=10; количество шарниров Ш=13; количество опорных связей C0 4 ;
W 310 2 13 4 0.
Т.е. необходимый признак геометрической неизменяемости выполняется. Диски (стержни) D1 , D2 , D3 , D5 и D6 образуют неизменяемый диск DI ,
который прикреплен к земле тремя связями.
Диски D4 , D9 , D10 образуют неизменяемый шарнирный треугольник DII , прикрепленный двумя связями к основному диску DI и одной связью к основанию. Однако расположение этих связей не удовлетворяет
24

условиям прикрепления одного диска, так как оси связей пересекаются в одной точке С. Поэтому диск DII может повернуться (рис. 1.33,г) вокруг
точки С. Следовательно, данная ферма геометрически изменяема.
1.6. Нагрузки и воздействия
Разработка расчетной схемы требует определенной идеализации внешних воздействий. Внешние воздействия могут иметь статический или динамический характер. Основные типы нагрузок – это:
1. Сосредоточенные силы (рис. 1.34). Как правило, это нагрузки, действующие на данную конструкцию со стороны других конструкций или тел.
Рис. 1.34. Нагрузки в виде сосредоточенных сил
2. Распределенные нагрузки (рис. 1.35). Например собственный вес, ветровая нагрузка.
Рис. 1.35. Нагрузки в виде распределенных воздействий
3. Сосредоточенные моменты (рис. 1.36)
Рис. 1.36. Нагрузки в виде сосредоточенных моментов
25

4. Тепловые воздействия (рис. 1.37). Например, разность температур внутри и снаружи здания.
Рис. 1.37. Температурные воздействия
5. Кинематические воздействия (смещение опорных закреплений) (рис. 1.38). Например, осадка фундамента.
Рис. 1.38. Осадка опоры
Статическая нагрузка не изменяется во времени или изменяется очень медленно, что не вызывает возникновения в сооружении сил инерции. При динамическом воздействии нагрузки изменяются во времени и влияние сил инерции может быть очень значительным.
Кроме того, нагрузки на сооружение могут быть постоянными и временными.
1.7. Физические свойства материалов элементов конструкции
Жесткостные параметры стержней зависят от механических свойств материалов. Механические свойства материалов определяются, как правило, диаграммами зависимости напряжение – деформация.
Будем различать следующие модели деформирования:
идеально упругое тело (рис.1.39,а);
жесткопластическое тело, определяемое диаграммой (рис 1.39,д); При расчете железобетонных конструкций или конструкций из других
композитных материалов могут быть использованы одновременно две или несколько зависимостей (рис 1.39,е).
26
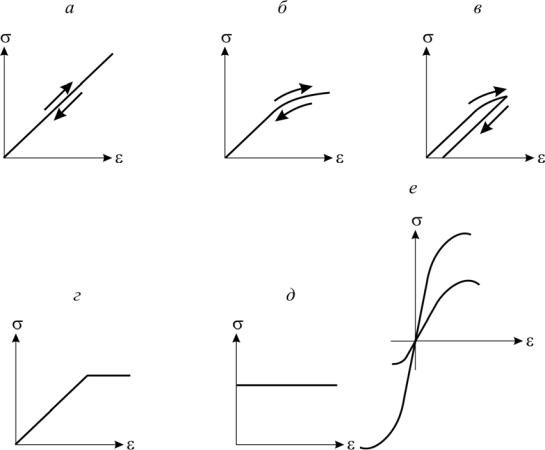
Рис. 1.39. Модели деформирования
Встроительной механике применяют и модели вязкоупругих тел, вязкоупругопластических тел и др.
Вдальнейших расчетах ограничимся рассмотрением линейно-упругих
тел.
1.8. Расчет статически определимых систем
на неподвижную нагрузку
Для определения усилий в сечениях статически определимых систем достаточно уметь составлять уравнения равновесия.
Определение усилий в произвольном сечении стержня или рамы производится из условий равновесия отсеченной части.
Продольная сила N в сечении равна сумме проекций всех внешних сил, приложенных по одну сторону от сечения, на касательную к оси стержня в рассматриваемом сечении. Продольная сила считается положительной, когда она вызывает в стержне растяжение, и отрицательной, когда вызывает сжатие.
Поперечная сила Q равна сумме проекций всех внешних сил, приложенных по одну сторону от рассматриваемого сечения, на нормаль к оси
27

стержня в рассматриваемом сечении. Поперечная сила в сечении считается положительной, если касательная к эпюре моментов разворачивается по отношению к оси по часовой стрелке.
Изгибающий момент М равен сумме моментов всех внешних сил, расположенных по одну сторону от рассматриваемого сечения, относительно точки сечения, лежащей на оси стержня. Ординаты эпюры изгибающих моментов откладываются со стороны растянутых волокон стержня.
Положительные направления усилий, приложенных к бесконечно малому элементу горизонтально ориентированного стержня, показаны на рис.1.40.
Рис. 1.40. Положительные направления усилий
Между нагрузкой, изгибающим моментом и поперечной силой существуют следующие дифференциальные зависимости:
Fky 0. Q q dx Q dQ 0.
M K
Откуда имеем:
0. M q (dx2)2 (Q dQ)dx M dM 0.
Q dMdx ;
q dQdx ;
q d 2M . dx2
(1.3)
(1.4)
(1.5)
Эпюру поперечных сил удобно строить по эпюре изгибающих моментов. При этом на линейных участках эпюры М поперечная сила определяется как тангенс угла наклона эпюры М к оси стержня. В местах приложения сосредоточенной силы эпюра М имеет перелом, острие которого направлено в сторону действия силы, а эпюра Q – скачок, равный проекции силы на нормаль к оси.
28

Пример №1. Построить эпюры M, Q, N в балке с осью ломаного очертания (рис. 1.41).
Рис. 1.41. Расчетная схема балки
1. Проведем проверку геометрической неизменяемости. Количество дисков D=1.
Количество шарниров Ш=0. Количество опорных связей C0 3.
W 31 0 3 0 .
Три связи не параллельны и не пересекаются в одной точке; значит, система статически определима и геометрически неизменяема.
2.Определим опорные реакции.
M A 0 2 1 6 1 4 6 RB 8 0; RB 328 4.
FKX 0. X A 1 0; X A 1 кН.
FKУ 0. УА 4 4 0; УА 0.
3.Построим эпюры внутренних усилий M, Q, N.
На левом горизонтальном участке бруса:
M I M лев 2 |
(кН м); |
|
QI |
FKnлев 0; |
|
N1 |
FK лев 1(кН). |
|
Аналогично рассуждаем для вертикального участка и для правого горизонтального участка.
По полученным значениям строим эпюры (рис. 1.42). Эпюру поперечных сил весьма удобно строить по эпюре моментов. При этом на линейных участках изменения момента поперечную силу Q M / l , т.е. перепад
29

момента, надо поделить на длину участка. На криволинейных участках эпюры моментов эпюру поперечных сил получаем на основе принципа независимости действия сил путем сложения эпюры от линейного изменения момента с эпюрой от распределенной нагрузки (рис. 1.43).
Рис. 1.42. Эпюры внутренних сил
Рис. 1.43. Построение эпюры поперечных сил на участке с криволинейным характером изменения эпюры моментов
Пример №2. Построить эпюры M, Q, N в балке (рис. 1.44).
К
Рис. 1.44. Расчетная схема балки
30
