Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2545

.pdf

Скачиваний:

Добавлен:

22.06.2024

Размер:

13.44 Mб

Скачать

☆

<<< < Предыдущая 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 2728 / 3228 29 30 31 32 > Следующая >>>

Конечный элемент на рисунке показан до и после деформации. Учитывая, что углы поворота в начальной i и конечной j точках стержня не меняются при преобразовании координат, получим:

ui ui cos vi sin ; vi ui sin vi cos; i i . (10.50) u j u j cos vj sin ; vj u j sin vj cos; j j .

В матричной форме эти зависимости можно записать в виде:

U TU ,

где

U ui vi i u j				vj	j T ,
U ui		vi i u j vj			j T ,
c		s	0	0	0	0
s		c	0	0	0	0
	0	0	1	0	0
						0	,
T	0	0	0	c	s
						0
	0	0	0	s	c	0
	0	0	0	0	0
						1

Т– матрица преобразования координат. Из соотношения (10.51) находим:

U T 1U .

(10.51)

(10.52)

(10.53)

(10.54)

Матрица преобразования координат является ортогональной матрицей,

т.е.

T 1 TT .	(10.55)
Следовательно,
U TT U .	(10.56)

Значение энергии не зависит от выбранной системы координат, т.е.

	1 T	1	T
	2U K U	2U		KU ,	(10.57)
где K –	матрица жесткости в локальной системе координат;
K –	матрица жесткости в глобальной или общей системе координат.
Но	(U )T (TU )T (U TTT ).
	(U )T (TU )T (U TTT ).				(10.58)
С учетом (10.58) соотношение (10.57) можно переписать в виде
	1U TTT K TU	1U T KU.			(10.59)
	2	2

271

Сравнивая левую и правую части уравнения (10.59), находим правило преобразования матрицы жесткости при изменении системы координат:

K TT K T.

(10.60)

Перед выполнением операции суммирования векторов перемещений и узловых нагрузок они преобразовываются к общей системе координат. Для i-го элемента эти преобразования имеют вид:

T
Ui Ti	Ui ,	(10.61)
P T T P.		(10.61)
P T T P.
i i	i
i i	i

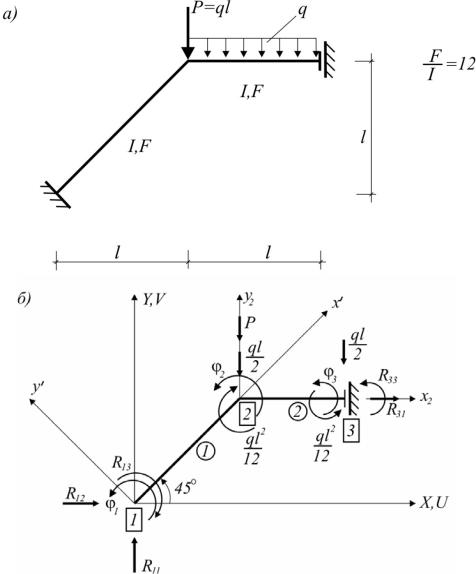
Пример № 3. Произвести расчет рамы, изображенной на рис. 10.10,а.

Рис. 10.10

272

Вектор угловых перемещений 1-го элемента: U1T u1v1 1 u2v2 2 . Для второгоэлемента: U2T u2v2 2 u3v3 3 . Векторперемещенийрамнойсистемы:

U T u1v1 1 u2v2 2 u3v3 3 .

Матрица жесткости 1-го элемента получается как комбинация двух ранее полученных матриц жесткости (10.19) при 0 и (10.49):

	EF						0				0			EF			0
		l					0				0			l			0
		1					12EI				6EI			1		12EI
		0					12EI				6EI			0		12EI
		0					3				2			0				3
								l1			l1						l1
											4EI			0			6EI
											l 3			0			l	2
	k1'										1		EF				1
													EF				0
														l1			0
														l1
					симметрично										12EI
					симметрично												l 3
																	1



Учитывая, что l					l /			2	l 2,		F 12, получаем:
Учитывая, что l					l /				l 2,		F 12, получаем:
			1				2				I
	6 2l2						2				I
	6 2l2				0					0		6 2l2					0
				3 2						3l				0	3			2
				3 2						3l				0	3			2
										2 2l2				0		3l
k'										2 2l2				0		3l
1													6	2l2			0
													6	2l2			0

								симметрично							3			2



						2				0		0		12l	2			0
			12l							0		0		12l				0
										12		6l		0			12
												4l	2	0			6l
	k2' k2											4l		0			6l
	k2' k2													12l2				0
														12l2				0
							симметрично										12
							симметрично										12

	0
6EI
6EI
	2
	l1
2EI
	l1
	l1	.
	0

	6EI
	l 2
	1
4EI
	l1
	l1

0
3l
3l
2l2	EI		;
0		l3	;

3l
2 2l2
2 2l2

2l2 EI .

0 l3 6l

4l2

273

Матрица преобразования координат для первого стержня имеет вид:

							2	2
									0	0	0	0
							2	2	0	0	0	0
с		s	0	0	0	0	2	2
с		s	0	0	0	0	2	2
					0		2	2	0	0	0	0
							2	2	0	0	0	0
s с 0 0						0	2	2	1	0	0
	0	0	1	0	0	0	0	0	1	0	0	0
T	0	0	0	с						2	2	.
	0	0	0	с	s 0		0	0	0	2	2	0
	0	0	0	s	s 0		0	0	0	2	2	0
	0	0	0	s	с	0				2	2
	0	0	0	0	0					2	2
	0	0	0	0	0	1	0	0	0	2	2	0
						1	0	0	0	2	2	0
										2	2
							0	0	0	0	0
							0	0	0	0	0	1

Тогда матрица жесткости первого стержня в глобальной системе координат примет вид:

			3 2	l2	1	3 2	l2		1		3 2 l		3 2	l2			1			3 2 l2					1			3 2 l
					2					2	2																			2
					2					2	2								2								2			2
						3 2		2		1	3 2	l	3 2			2			1					2			1	3 2			l
						3 2	l			2	2	l	3 2	l						3 2 l									2		l
										2	2								2								2		2
													3 2 l									3 2 l
k1 T	T	'									2 2l2		3 2 l									3 2 l							2l2				EI
k1 T		k1T												2								2												l	3 .
																		1								1		3		2				l
						симметрично									2			1		3	2		2			1		3		2	l
						симметрично							3 2 l					2		3	2	l				2			2		l
																		2								2			2

																				3	2		2			1			3	2		l
																				3	2	l				2				2		l
																										2				2
																												2		2l	2
																												2		2l

Поскольку локальная система координат элемента 2 совпадает с универсальной системой, то матрицу жесткости элемента 2 не следует тран-

сформировать (k2 k2' ) .

Матрица жесткости K образуется внесением на соответствующие позиции элементов матриц k1 и k2 , их суммированием Ki j ki j , когда в

каждой ячейке появятся элементы обеих матриц:

274

3 2	l2	1	3 2	l2		1		3 2 l		3 2		l2			1				3 2		l2					1		3 2 l				0			0	0
		2					2	2									2												2
		2					2	2									2									2			2
					2		1	3 2						2			1						2			1			3 2
			3 2		2		1	3 2	l	3 2				2			1		3 2				2			1			3 2		l	0			0	0
			3 2	l			2	2	l	3 2		l					2		3 2		l								2		l	0			0	0
							2	2									2									2			2
								2 2l2			3 2 l									3 2 l									2 l2
								2 2l2			3 2 l									3 2 l									2 l2			0			0	0
												2									2
											2		1					2				2			1				3 2					2				EI
K										3 2 l			2			12l			3 2	l									2		l	12l			0	0
K										3 2 l						12l			3 2	l											l	12l			0	0			3
																									2													l
																								1				3 2
								симметрично												2				1		12		3 2		l	6l	0			12	6l
								симметрично											3 2 l							12			2	l	6l	0			12	6l
																								2					2
																											2 2l2 4l2					0			6l
																											2 2l2 4l2					0			6l	2l2
																																12l	2		0	0
																																12l			0	0
																																			12 6l
																																				4l	2
																																				4l

Узловые силы рамной системы складываются из внешних нагрузок и реакций:

		0 R11
		0 R12						0
		0 R12
		0 R13						0
		0 R13						0
				0				0
				0				0
								0
		1
		1
		2		ql P			1,5
		2					1,5
P			1					1			ql	R	.
					ql2					l
								12

		12
		0 R31						0


				1 ql			0,5
							0,5
								1
				2				1	l
	1

		ql2 R					12
		ql2 R					12
12						33

Заменяя в матрице K и векторе P длину l на 4 и разделяя систему уравнений KU P согласно неизвестным, а также известным величинам в векторе параметров перемещений, получаем следующую систему уравнений:

275

	262,004		65,761	8, 485	0	\|	70,004	65,761	8,845	192
		65,761	82,004	15,515	12	\|	65,761	70,004	8, 485	0
		8, 485	15,515	109, 255	24	\|	8, 485	8, 485	22,627	0

		0	12	24	12	\|	0	0	0	0

EI		\|
l3			65,761	8, 485	0	\|	70,004	65,761	8, 485	0
	70,004
		65,761	70,004	8, 485	0	\|	65,761	70,004	8, 485	0
		8, 485	8, 485	22,627	0	\|	8, 485	8, 485	45, 255	0

		192	0	0	0	\|	0	0	0	192

		0	24	32	24 \|		0	0	0	0

	0			0
	1,5			0
	1,5			0
0,33				0
	0,5			0
	0,5			0

		ql			.
	0		R11
	0		R
				11
	0		R13
	0		R
	0,33			31
	0,33		R
				33

0	u2
24	v
		2
32		2
24
24	v3

0
0	u1
0		v
		1
0		1
0	u
64		3
64
		3

Решая систему из четырех линейных алгебраических уравнений с четырьмя неизвестными

262,004	65,761	8,485	0	u2		0
	82,004	15,515	12	v		1,5
EI		109,255		2			ql ,
l3		109,255	24	2	0,333
			12	v		0,5
				3

получаем значения неизвестных параметров перемещений в узлах системы:

u2		0,0118
v	0,0432				4
2			ql
2	0,0294			EI .
v		0,1436
3

276

Затем определяем реакции опор:

R11	70,004		65,761	8,485
R		65,761	70,004	8,485
12		8,485	8,485	22,627
R13		8,485	8,485	22,627
R		192	0	0
31
R		0	24	32
33

0		0,0118		0
0		0,0118		0
0				0
0	0,0432 ql			0	ql;
0	0,0294			0
0		0,1436		0
		0,1436
24			0,333

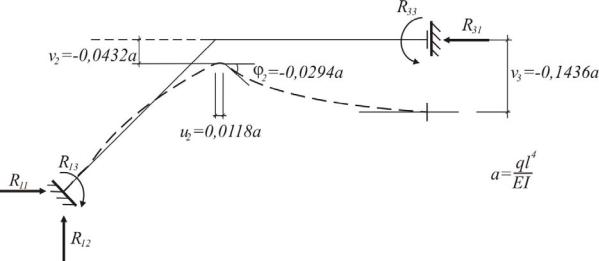
Рис. 10.11. Схема перемещений рамы

Реакции, соответственно, равны:

R11			2,264
R			2,000
12
R13			0,198 ql.
R			2,265
31
R			1,136
33

Полученные значения параметров перемещения, реакции опоры, диаграммы перемещений и момента изгиба показаны на рис.10.11.

277

10.8. Решение плоской задачи теории упругости МКЭ. Треугольный элемент

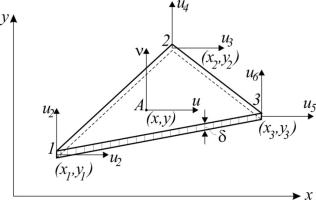
Рассмотрим элемент в виде произвольного треугольника (рис.10.12).

Рис. 10.12

Поле перемещений точек A(x, y) треугольника зададим в виде

полиномов, число неизвестных коэффициентов которых (шесть) равно числу степеней свободы элемента.

u (x, y) a bx cy;							(10.62)
v(x, y) d ex					fy.		(10.62)
v(x, y) d ex					fy.
Вектор узловых перемещений имеет вид:
U u u	2	u u	4	u u		T .	(10.63)
1	2	3	4	5	6

Выразим поле перемещений через перемещения узловых точек треугольника. Получим 6 уравнений:

	u1 a bx1 cy1;
	u3 a bx2 cy2;
	u5 a bx3 cy3;	(10.64)
	u2 d ex1 fy1;	(10.64)
	u2 d ex1 fy1;
	u4 d ex2 fy2;
	u6 d ex3 fy3.

Сделаем следующие обозначения. Площадь треугольника обозначим F. Выразив ее через координаты вершин треугольника, получим:

F	1[(x		x )( y		y ) ( y	2	y )(x		x )].	(10.65)
	2	2	1	3	1	2	1	3	1
	2

278

Разности координат отдельных вершин обозначим следующим

	образом:
	c1 s2 y3 y2;
	c2 s1 x2 x3;
	c3 s4 y1 y3;	(10.66)
	c4 s3 x3 x1;	(10.66)
	c4 s3 x3 x1;
	c5 s6 y2 y1;
	c6 s5 x1 x2.

Решив систему уравнений для узловых перемещений (10.64) относительно коэффициентов b,c,e и f , получим:

	b (c1u1 c3u3 c5u5 ) / (2F);
	c (s1u1 s3u3 s5u5 ) / (2F);	(10.67)
	e (s2u2 s4u4 s6u6 ) / (2F);	(10.67)
	e (s2u2 s4u4 s6u6 ) / (2F);
	f (c2u2 c4u4 c6u6 ) / (2F).

Используя уравнения для поля перемещений (10.62), построим поле деформаций. Относительные удлинения и относительный сдвиг можно записать в виде:

x u b;x

y v f ; (10.68)y

xy u v c e.y x

Эти деформации вызывают растягивающие напряжения x , y в направлении осей x и y, а также касательное напряжение xy . Зависимость между этими напряжениями и деформациями описывается законом Гука:

	x	2G	( x y )
		1

	y	2G	( y x )
		1

	xy G xy G(c e),
где G –	модуль сдвига;
–	коэффициент Пуассона.

2G (b f );

2G ( f b); (10.69)

279

Модуль сдвига связан с модулем упругости Е соотношением

(10.70)

2(1 )

В единице объема элемента заключена упругая энергия, равная

1 ( x x

y y xy xy ),

(10.71)

а поскольку элемент имеет толщину

и объем

F , то потенциальная

энергия всего элемента n будет равна:

1 F(

)

. (10.72)

(c e)

b(b f ) f ( f

Подставляя выражения b,c,e и f , получаем:

			6	6
		Vn	1 kijuiu j ,				(10.73)
			2 i 1	j 1
или в матричной форме
		V 1U T k U.					(10.74)
		n	2	n
			2
Можно проверить, что коэффициенты kij ,					представляющие собой эле-
менты матрицы жесткости kn , описываются уравнением
k	G 1 ( 1)i k c c				s s	.	(10.75)
ij				i k	i	k
	4F 1

Потенциальная энергия деформации всей конструкции равна сумме упругих энергий ее элементов

kn U

T N

KU ,

(10.76)

V Vn

kn U

n 1

где K матрица жесткости всей конструкции, представляющая собой сумму матриц жесткости ее элементов,

N
K kn .	(10.77)

n 1

280

<<< < Предыдущая 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 2728 / 3228 29 30 31 32 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.06.202413.26 Mб02540.pdf
#
22.06.202413.27 Mб02541.pdf
#
22.06.202413.37 Mб02542.pdf
#
22.06.202413.4 Mб02543.pdf
#
22.06.202413.4 Mб02544.pdf
#
22.06.202413.44 Mб42545.pdf
#
22.06.202413.7 Mб02546.pdf
#
22.06.202413.72 Mб02547.pdf
#
22.06.202413.77 Mб02548.pdf
#
22.06.202413.77 Mб02549.pdf
#
17.06.2024251.51 Кб0255.pdf