Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2545

.pdf

Скачиваний:

Добавлен:

22.06.2024

Размер:

13.44 Mб

Скачать

☆

<<< < Предыдущая 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 2627 / 3227 28 29 30 31 32 > Следующая >>>

10.4. Пример расчета фермы МКЭ

Пример . Произведем расчет фермы МКЭ (рис. 10.4)

Рис. 10.4

Вектор перемещений данной системы имеет вид:

					и и и		2	и и		4	и и			6	и	7	и	T .
					1		2	3		4		5		6		7	8
	Примем EFi			/ li 2 .
	Матрицы жесткости отдельных элементов можно записать в виде
следующих таблиц:
		I							II												III
	1	2	3	4				3	4				5		6					3	4	7	8
	1	2	3	4				3	4				5		6					3	4	7	8
1	2	0	-2 0			3		2	0				-2 0						3	0	0	0	0
2	0	0	0	0	4			0	0				0		0			4		0	2	0	-2
3	-2 0		2	0	5			-2 0					2		0			7		0	0	0	0
4	0	0	0	0	6			0	0				0		0			8		0	-2 0 2

		IV						V
	1	2	7	8			5	6	7	8
	1	2	7	8			5	6	7	8
1	1	1	-1 -1			5	1	-1 -1		1
2	1	1	-1 -1		6		-1	1	1	-1
7	-1 -1		1	1	7		-1	1	1	-1
8	-1 -1		1	1	8		1	-1 -1		1

261

Матрица жесткости фермы представляет собой сумму матриц жесткостей её элементов:

		1	2	3		4	5	6	7	8
1	3		1	-2 0			0	0	-1 -1
2	1		1	0	0		0	0	-1 -1
3	-2 0			4	0		-2 0		0	0
K= 4	0		0	0	2		0	0	0	-2
5	0		0	-2 0			3	-1 -1 1
6	0		0	0	0		-1 1		1	-1
7	-1 -1 0				0	-1 1			2	0
8		-1 -1		0	-2		1	-1	0	4

Рис. 10.5

Уравнения равновесия можно записать в виде:

Р1 3и1 1и2 2и3 0и4 0и5 0и6 1и7 1и8;

Р3 1и1 1и2 0и3 0и4 0и5 0и6 1и7 1u8;

Р3 2и1 0и2 4и3 0и4 2и5 0и6 0и7 0и8; Р4 0и1 0и2 0и3 2и4 0и5 0и6 0и7 2и8;

Р5 0и1 0и2 2u3 0и4 3и5 1и6 1и7 1и8;

Р6 0и1 0и2 0и3 0и4 1и5 1и6 1и7 1и8; Р7 1и1 1и2 0и3 0и4 1и5 1и6 2и7 0и8; Р8 1и1 1и2 0и3 2и4 1и5 1и6 0и7 4и8.

262

При этом вектор
P1		0 R1
P2	100 R
		2
P3		0
		100
P4		100
P P		0	.
5
P		100 R
6		6
P7		0
P		0
8

Для вычисления перемещений и3, и4, и7, и8 систему уравнений перепишем в виде:

Р3 2и1 0и2 4и3 0и4 2и5 0и6 0и7 0и8;Р4 0и1 0и2 0и3 2и4 0и5 0и6 0и7 2и8;Р7 1и1 1и2 0и3 0и4 1и5 1и6 2и7 0и8;

Р8 1и1 1и2 0и3 2и4 1и5 1и6 0и7 4и8.

Здесь и1 = и2 = и6 =0, и5=1.

Подставив Pi и иi , получим следующий вид системы уравнений:

2 4и3 0и4 0и7 0и8;100 0и3 2и4 0и7 2и8;1 0и3 0и4 2и7 0и8;

1 0и3 2и4 0и7 4и8.

Откуда

и3=0,5; и7 =0,5; и8=-50,5; и4=-100,5.

Определение усилий в элементах производится по формуле

N EFl l EFl [(u2 u1)c (v2 v1)s].

Например, для стержня IV получим:

N 2[(u7 u1)0,707 (u8 u2 )0,707]

2 0,5 0,707 ( 50,5) 0,707 70,7.

263

10.5. Расчет МКЭ конструкций из изгибаемых элементов стержневого типа

Перемещения изгибаемой балки определяются перемещениями w1 и w2 и углами поворота 1 и 2 оси балки на концах (рис. 10.6).

Рис. 10.6

Сгруппируем их в вектор обобщенных перемещений:

U 1 . (10.39)w

Прогиб оси балки в точке А, лежащей на расстоянии x от конца балки, описывается полиномом третьей степени

w a bx cx2 dx3 .

(10.40)

Этот полином является точной формулой прогиба балки, если принять, что силы и моменты действуют только на ее концах. Коэффициенты а, в, с,

d полинома определяются из граничных условий
w(0) w1; w (0) 1; w(l) w2; w (l) 2 .				(10.41)
Подставив граничные условия в уравнение (10.30), получим систему
уравнений:
w1 a;
1 в;
1 в;				(10.42)
w a bl cl2 dl3			;	(10.42)
2
2 b 2cl 3dl	2	.
2 b 2cl 3dl		.

264

Решение этой системы имеет вид:

					a w1;
					b 1;
					b 1;																	(10.43)
					с ( 3w			2 l 3w							2	l) / l			2;			(10.43)
						1				1		2			2
					d (2w		l			2w			2	l) / l3.
						1		1			2		2
Кривизна изогнутой оси стержня определяется выражением
					w 2c 6dx 2(c 3dx).																	(10.44)
Ее вызывает изгибающий момент
					M g EJ 2EJ (c 3dx).																	(10.45)
Упругая энергия изгиба балки при статическом нагружении запи-
сывается в виде:
V 1 l		M g	dx		1 l 4EJ (c 3dx)2 dx
2					2
	0				0																	(10.46,а)
	l																					(10.46,а)
2EJ (c2			6c d x 9d 2 x2 )dx 2EJ (c2l 3cdl2 3d 2l3 ).
	0
После подстановки значений c и d из (10.33) и преобразований
получим:
V	2EJ		3w12 3 lw1 1 6w1w2									3 lw1 2 l2 12										(10.46,б)
V		l3		3	l w l2 3w2							3 lw l								2 2	.	(10.46,б)
		l3		3	l w l2 3w2							3 lw l								2 2
					1	2		1	2		2					2		2
					1	2		1	2		2					2		2		2
Это выражение можно записать в матричной форме
						V	1U T			k U ,												(10.47)
							2
где k – матрица жесткости балки,
								6		3l		6				3l
						2EJ		3l		2l	2	3l				l	2
					k	2EJ		3l		2l		3l				l			.			(10.48)
					k	l3	6			3l		6 3l							.			(10.48)
						l3	6			3l		6 3l
								3l		l2		3l			2l2
								3l		l2		3l			2l2

Формирование матрицы жесткости всей системы и решение системы уравнений МКЭ производятся по тем же правилам, что были использованы при расчете ферм.

265

Матрица жесткости для элемента с тремя степенями свободы

[сначала (предположим, слева) – жесткий узел, справа – шарнирный узел] будет иметь вид:

		3EI
		l3
		3EI
k		3EI
k		l2
		l2

	3E3I
		l
		l

3EI				3EI
	l2				l3
3EI
3EI				3EI		.	(10.49,а)
	l				l2	.	(10.49,а)
	l				l2
	3EI		3EI
	3EI		3EI
	l	2		l	3
	l			l

Если слева – шарнир, а справа – жесткий узел, то матрица жесткости такого конечного элемента имеет вид:

3EI

(10.49,б)

3EI

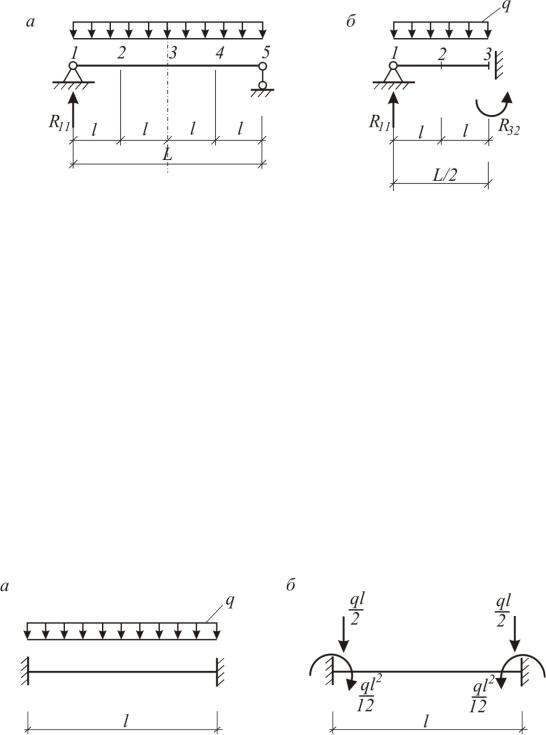
10.6. Пример расчета балки МКЭ

Вычислимперемещениябалки, изображеннойнарис.10.7. Разобьембалкуна четыре конечных элемента одинаковой длины. Поскольку балка и нагрузка на нее симметричны, рассмотрим только половину, т.е. два конечных элемента из

четырех. Матрицыжесткости(безкоэффициента 2lE3I ) приведеныниже:

		w1
w1		6
		3l
1
k1 w	6
2		3l
2		3l
		w2
		w2
w2		6
k2 2	3l
w3		6
3		3l
3		3l

1	w2	2
3l	6	3l
2l2	3l	l2		;
3l	6	3l		;
3l	6	3l
l2	3l	2l2
l2	3l	2l2
2	w3	3
2	w3	3
3l	6	3l
2l2	3l	l2	.
3l	6	3l
l2	3l	2l2
l2	3l	2l2

266

Рис. 10.7

Матрица жесткости балки (половины) будет иметь вид:

			6	3l	6	3l	0	0
		3l		2l2	3l	l2	0	0
K	2EI		6	3l	12	0	6	3l
K	l3		3l	l2	0 4l2		3l	l2
	l3		3l	l2	0 4l2		3l	l2
			0	0	6	3l	6	3l

		0		0	3l	l2	3l	2l2 .

Уравнения равновесия в матричной форме записаны в виде:

KU P .

Здесь вектор Р формируется из приведенных к узлам сил и моментов от равномерно распределенной нагрузки (рис.10.8,а,б):

Рис. 10.8

	1/ 2			1/ 2
	(1/12)l		P	(1/12)l
P		ql .	P		ql .
1	1/ 2		2	1/ 2
	1/ 2			1/ 2
	(1/12)l			(1/12)l
			267

Вектор узловых сил для рассчитываемой балки:

										1/ 2
										(1/12)l

						P					1					ql R,
											0
										1/ 2
										(1/12)l
где R – вектор реакций,
									R11										0
										0									0
						R					; R
								1		0					2				0
										0								R
																			32	;
												R11
														0

										R				0			.
														0
														0
												R32
Итак, уравнение KU P будет иметь вид:
	6	3l			6	3l				0			0					w1				01/ 2						R11
	3l	2l		2	3l	l	2			0			0						1			(1/12)l							0
	3l	2l			3l	l				0			0						1			(1/12)l							0
2EI	6	3l			12	0 6 3l												w2				1							0
	3l	l2			0	4l2			3l				l2						2				0				ql		0
l3	3l	l2			0	4l2			3l				l2						2				0						0
	0	0			6	3l				6		3l						w				1/ 2							0
	0	0			6	3l				6		3l							3									R
																						(1/12)l
	0	0			3l	l		2	3l			2l			2							(1/12)l
	0	0			3l	l			3l			2l							3										32
Исключив уравнения, содержащие реакции, получим:
			2l2		3l			l2		0			1						(1/12)l
			3l 12					0		6			w								1			ql	3
															2									ql		.
				l2	0 4l2					3l				2							0			2EI		.
				0	6		3l			6			w3							1/ 2

268

Отсюда

		16
	1		383	l	ql	3
	w			l	ql
	2		8				.
	2	226			2EI		.
w			20 l
	3		3

Затем можно определить реакции:

163

38 l

1/ 2

R32

226

(1/12)l

203 l

R11

ql.

В случае, когда определять угол поворота балки над левой опорой не надо, можно воспользоваться матрицей жесткости (10.49,б). Тогда вектор

перемещений U v1 v2	2 v3	3 T .
Вектор узловых сил	P	3ql	9ql	ql2	ql	ql2	T .
		8	8	24	2	12

		1.5	1.5	1.5l
k	2EI 1.5		1.5	1.5l		.
1	l3
		1.5	1.5l	1.5l	2
		1.5	1.5l	1.5l

269

Складываем матрицы k1 и k2 . Поскольку перемещения v1 и 3 извест-

ны, определяем перемещения v2 2 v3 . Система уравнений решается в

Mathcad:

Given

15 w2

9 q

w2 7

(

19 l4

8 EI

11 l3

Find(w2 2 w3)

6 EI

10 l4

Результаты решения те же.

10.7. Преобразование координат

Для некоторых конечных элементов матрицы жесткости выводятся в местной системе координат, оси которой ориентированы отлично от общей системы. Поэтому при формировании общей матрицы жесткости, общего вектора перемещений и общего вектора узловых сил необходимо сделать переход от местной к общей системе координат.

Например, для сжато-изогнутого стержня, входящего в состав плоской стержневойсистемы(рис. 10.9), каждыйузелимееттристепенисвободы: u,v, .

Рис. 10.9

270

<<< < Предыдущая 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 2627 / 3227 28 29 30 31 32 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
22.06.202413.26 Mб02540.pdf
#
22.06.202413.27 Mб02541.pdf
#
22.06.202413.37 Mб02542.pdf
#
22.06.202413.4 Mб02543.pdf
#
22.06.202413.4 Mб02544.pdf
#
22.06.202413.44 Mб42545.pdf
#
22.06.202413.7 Mб02546.pdf
#
22.06.202413.72 Mб02547.pdf
#
22.06.202413.77 Mб02548.pdf
#
22.06.202413.77 Mб02549.pdf
#
17.06.2024251.51 Кб0255.pdf

1	w2	2
3l	6	3l
2l2	3l	l2		;
3l	6	3l		;
3l	6	3l
l2	3l	2l2
l2	3l	2l2
2	w3	3
2	w3	3
3l	6	3l
2l2	3l	l2	.
3l	6	3l
l2	3l	2l2
l2	3l	2l2

1	w2	2
3l	6	3l
2l2	3l	l2		;
3l	6	3l		;
3l	6	3l
l2	3l	2l2
l2	3l	2l2
2	w3	3
2	w3	3
3l	6	3l
2l2	3l	l2	.
3l	6	3l
l2	3l	2l2
l2	3l	2l2

1	w2	2
3l	6	3l
2l2	3l	l2		;
3l	6	3l		;
3l	6	3l
l2	3l	2l2
l2	3l	2l2
2	w3	3
2	w3	3
3l	6	3l
2l2	3l	l2	.
3l	6	3l
l2	3l	2l2
l2	3l	2l2