Сопоставив, получим: Рпр Рi min Р1 267 М0.
В заключение отметим, что в 3- и 4-стержневых узлах пластический шарнир образуется в загруженном стержне, если
n
Mзагр0 Mi0 , i 1
где п – количество остальных стержней в узле.
В противном случае пластические шарниры возникают на концах всех остальных стержней.
222
S3 F 0.
S4 F4 0;
9. МАТРИЦЫ В СТРОИТЕЛЬНОЙ МЕХАНИКЕ. МЕТОД ПЕРЕМЕЩЕНИЙ В МАТРИЧНОЙ ФОРМЕ
9.1. Связь между внешними и внутренними силами. Матричные уравнения равновесия
Рассмотрим простую шарнирно-стержневую систему (рис. 9.1,а).
Введем вектор узловых нагрузок |
|
P F F F F F T 0 0 0 0 F T , |
|
|
|
|
|
1 |
2 |
3 |
4 |
вектор узловых перемещений Z z z |
2 |
z z |
4 |
z |
T |
, а также векторы внутрен- |
1 |
3 |
5 |
|
|
|
|
них усилий S S1S2S3S4S5 T и деформаций элементов E e1 e2 e3 e4 e5 T в соответствии с рис. 9.1,б. Заметим, что эти векторы составляются в соответствии с заданной расчетной схемой системы.
Рис.9.1
Вырезая последовательно по часовой стрелке узлы фермы и составляя уравнения равновесия
|
Fkx 0; |
Fky |
0, |
|
(9.1) |
получим систему уравнений равновесия вида: |
|
|
S1 |
F1 0; |
|
|
|
|
S |
S |
5 |
cos F |
0; |
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
(9.2) |
S3 S5 sin F3 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Перепишем эти уравнения равновесия в матричной форме:
1 |
0 |
0 |
0 |
0 |
|
S1 |
|
0 |
0 |
|
|
0 |
1 |
0 |
0 |
cos |
S |
2 |
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
1 |
0 |
sin |
S3 |
|
|
0 |
|
0 . |
(9.3) |
|
0 |
0 |
0 |
1 |
0 |
|
|
|
|
|
0 |
|
|
|
|
|
S4 |
|
|
|
0 |
|
|
0 |
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
S5 |
|
F |
0 |
|
Это соотношение можно переписать в более компактном виде: |
|
|
|
|
|
AS P 0, |
|
|
|
|
|
|
(9.4) |
где А – матрица системы статических уравнений.
Эту систему уравнений можно рассматривать как соответствие каждой внешней силе (из совокупности внешних сил F1, F2 ,..., Fn для линейно-уп-
ругой системы) некоторого распределения внутренних усилий S1, S2 ,..., Sm :
ai1S1 ai2S2 ai3S3 ... aimSm Fi 0 . |
(9.5) |
Полный расчет любой механической системы наряду с нахождением распределения усилий подразумевает определение деформаций и перемещений в ней.
9.2. Связь между деформациями и перемещениями. Матрицы податливости и жесткости
Возникающие в стержневых системах деформации вызывают перемещение их элементов. Причем, в силу того что после деформации системы сплошность ее не нарушается, перемещения узлов стержневой системы должны быть совместными с возникающими деформациями элементов, и наоборот. Эти условия совместности могут быть получены, исходя из чисто геометрических соображений. Для примера рассмотрим деформацию удлинениястержня, сопровождающуюсяперемещениямиегоконцов(рис. 9.2, а).
Считая перемещения малыми по сравнению с длиной стержня, для удлинения ∆l можно составить следующее выражение (рис. 9.2, б):
∆l = (u2 – u1) cos α + (υ2 – υ1) sin α. |
(9.6) |
Вводя новые обозначения u1 |
=z1, υ1 = z2, u2 =z3, υ2 = z4, ∆l = e, пере- |
пишем (6.6) в виде |
|
|
cos (α) z1 +sin (α) z2 |
– cos (α) z3 – sin (α) z4 + e=0. |
(9.7) |
Рис.9.2
Для произвольной стержневой системы можно составить т таких соотношений, где число т определяется количеством деформаций элементов. В общем случае размерность п вектора перемещений не совпадает с размерностью т(т ≥ п) вектора деформаций, за исключением статически определимых систем, для которых всегда выполняется равенство т = п. Поэтому совокупность соотношений вида (9.7) для произвольной стержневой системы может быть записана в виде
b11 z1 + b12 z2 +…b1n zn +e1=0, b21 z1 + b22 z2 +…b2n zn +e2=0,
bm1 z1 + bm2 z2 +…bmn zn +em=0.
Эти соотношения определяют геометрическую картину деформирования стержневой системы, и поэтому их принято называть геометрическими уравнениями.
В матричной форме эти уравнения могут быть представлены в виде
где B – в общем случае прямоугольная матрица размерности т п; Z – вектор узловых перемещений;
E – вектор деформаций элементов системы.
Из уравнений (9.8) можно исключить п перемещений; тогда оставшиеся (т – п) соотношений между деформациями будут являться уравнениями неразрывности деформаций. Эти уравнения накладывают определенные условия на выбор компонентов вектора деформаций, в силу чего этот вектор не может быть задан произвольно.
Для статически определимых систем т = п и уравнения неразрывности деформаций отсутствуют. В этом случае допускается произвольный выбор вектора деформаций. Заметим кстати, что этот случай реализуется при
224
температурных воздействиях. Здесь в силу условия P=0 внутренние усилия получаются нулевыми. Однако при ненулевых деформациях элементов решение системы уравнений (9.8) дает вполне определенное поле перемещений, характеризующих изменение геометрии конструкции.
Из уравнения (9.8) вытекает еще одно свойство статически определимых систем, которое состоит в том, что при нулевом поле деформаций E все перемещения обращаются в нуль, т.е. при этом система является геометрически неизменяемой.
Для деформаций удлинения элементов (см. рис. 9.1,б) имеем e1 = z1; e2 = z2; e3 = (z3 – z5);
|
|
e4 = z4; e5 = z2 cosα + z3 sinα. |
|
|
|
(9.10) |
В матричной форме уравнения (9.10) запишутся в виде |
|
1 |
0 |
0 |
0 |
0 |
z1 |
|
e1 |
|
0 |
|
|
0 |
1 |
0 |
0 |
0 |
z |
2 |
|
e |
|
0 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
0 |
0 |
1 |
0 |
1 |
z3 |
|
e3 |
|
0 |
(9.11) |
|
0 |
0 |
0 |
1 |
0 |
z |
4 |
|
e |
|
0 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
0 |
cos |
sin |
0 |
0 |
z |
5 |
|
e |
|
0 |
|
|
|
|
|
|
|
|
|
5 |
|
|
|
Из (9.3) и (9.11) непосредственно следует, что матрица системы геометрических уравнений В (9.3) является транспонированной по отношению к матрице системы статических уравнений А (9.11), и наоборот. Таким образом, имеем
В этом состоит свойство двойственности статических и геометрических уравнений стержневых систем. Строгое доказательство свойства двойственности приведено в подразд. 9.3.
Для статически определимой системы матрицы коэффициентов уравнений равновесия (9.4) и геометрических уравнений (9.9) являются квадратными. Эти матрицы обладают свойством двойственности, состоящим в том, что, зная одну из этих матриц, можно построить другую. Вообще говоря, свойство двойственности статических и геометрических уравнений оказывается справедливым для любой стержневой системы.
Пусть d11 – деформация от единичного усилия S1 по направлению S1, а dik – деформация от единичного усилия Sk по направлению Si. Тогда для статически определимой стержневой системы при известном распределении внутренних усилий S1,S2,…,Sm, на основании принципа независимости действия сил любая деформация ei может быть представлена в виде:
ei = di1 S1+di2 S2 +…+dim Sm, (i=1,2,…,m). |
(9.13) |
В матричной форме система соотношений (9.13) может быть записана в виде
Квадратная неособенная матрица D называется матрицей внутренней податливости.
Рассматривая (9.14) как систему линейных алгебраических уравнений, можно получить ее решение в виде
|
S D 1 |
|
. |
(9.15) |
|
E |
Обозначим |
D 1 [K]. |
(9.16) |
Квадратная неособенная матрица [K] называется матрицей внутренней жесткости. Элементы этой матрицы kik представляют собой внутренние усилия в i-м элементе от единичного значения k-й деформации. С учетом (9.16) выражение (9.15) перепишем в виде:
Между матрицей внутренней податливости и матрицей внутренней жесткости существует очевидная взаимосвязь
D =[K]-1; [K] =D-1 , |
(9.18) |
которая вытекает из условий однозначной разрешимости систем уравнений
(9.15) и (9.17).
При изучении стержневых систем особо важную роль играют продольные и изгибные деформации, вызванные растяжением или сжатием стержней и их изгибом. В дальнейшем под параметром продольной деформации будем понимать удлинение (укорочение) стержня, вызванное действием продольной силы, а под параметрами изгибной деформации – углы поворота φ поперечных сечений стержня или углы сдвига .
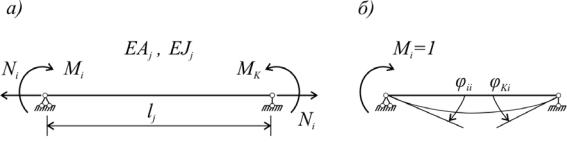
Приведем пример построения матриц внутренней податливости и внутренней жесткости для простейшей системы, изображенной на рис. 9.3, а.
Рис.9.3
Пусть в качестве компонентов вектора внутренних усилий выступают продольная сила Ni и концевые изгибающие моменты Mi и Mk, т.е. вектор S
S Ni , Mi ,Mk T . Тогда в качестве компонентов вектора деформаций следует принять удлинение ∆ стержня и углы поворота φi, φk концевых сечений: E , i , k T Вычислим элементы матрицы D, пользуясь известны-
ми из курса сопротивления материалов сведениями. Согласно формулам сопротивления материалов имеем:
d11 EAl j j ; d12 d13 0.
Прикладывая единичный момент Mi = 1, определяем φii и φki:
φii = d22 = |
l j |
; φki = d23= |
l j |
. |
3EJ j |
|
|
|
6EJ j |
Здесь коэффициент d21 будет равен нулю в силу предположения о нерастяжимости оси стержня при его изгибе. Аналогично получаем:
d31 = 0; d32 = |
l j |
.; d33 = |
l j |
. |
(9.21) |
6EJ j |
|
|
|
3EJ j |
|
Выражения (9.19) – (9.21) позволяют записать матрицу внутренней податливости для рассматриваемого примера в следующем виде:
|
l j |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
EJ j |
|
|
|
|
|
|
|
|
|
|
|
|
l j |
|
|
|
l j |
|
|
|
Dj |
0 |
|
|
|
|
|
. |
(9.22) |
|
3EJ j |
|
|
|
|
|
|
|
|
|
6EJ j |
|
|
|
|
l j |
|
|
|
l j |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
6EJ |
j |
|
|
3EJ |
|
|
|
|
|
|
|
|
|
|
j |
|
Построив обратную матрицу D-1 = k, находим матрицу внутренней жесткости стержня с наложенными по концам моментными связями:
|
EJ j |
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4EJ |
j |
|
|
2EJ |
j |
|
|
k j Dj |
1 |
0 |
|
|
|
|
|
. |
(9.23) |
|
|
l j |
|
|
l j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2EJ j |
|
4EJ j |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l j |
|
|
|
|
l j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если стержень на одном из концов закреплен шарнирно (Mi=0 или
Mk=0), то
|
EJ j |
0 |
|
|
|
|
|
|
|
|
l j |
|
k j |
|
3EJ |
|
. |
|
|
|
|
j |
|
|
|
0 |
|
|
|
|
|
l j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если оба конца стержня шарнирные, то
Выражения (9.22) – (9.25) справедливы для одного стержня. Если имеется совокупность таких стержней, объединенных в некоторую стержневую систему, то для этой системы матрицы внутренней жесткости записываются в виде блочных диагональных матриц, в которых каждый из блоков будет иметь вид соответственно (9.23), (9.24) или (9.25).
[K] – матрица жесткости всех не связанных между собой элементов, составляющих систему. Эта матрица, устанавливающая связь между внутренними факторами системы (искомыми усилиями и деформациями),
может быть названа матрицей внутренней жесткости системы и
представлена в виде:
k1 |
0 ... |
|
0 |
k2 ... |
[K] |
|
. . |
. |
|
0 |
0 ... |
|
Можно видеть, что матрица внутренней жесткости системы является квазидиагональной матрицей, элементами которой, расположенными на главной диагонали, являются матрицы жесткости отдельных стержней. Для ферм этими элементами будут матрицы первого порядка (т.е. числа) (9.25), для рам – матрицы второго или третьего порядка (9.24) или (9.23). Естественно, что матрица [K] – это квадратная матрица, общий порядок которой равен т (числу неизвестных усилий).

9.3. Обобщенные силы и обобщенные перемещения. Принцип возможных перемещений.
Двойственность уравнений в статически определимых системах
Механическая работа определяется как величина, численно равная произведению силы на перемещение точки приложения этой силы по ее направлению. Понятие сосредоточенной силы, фигурирующее в этом определении, как известно, является лишь частным случаем силового воздействия на сооружение. Поэтому есть смысл расширить понятие силы, имея в виду любое силовое воздействие – силу, момент, распределенную нагрузку, группу сил и группу моментов, а также различные их комбинации.
Такое обобщенное понятие внешнего силового воздействия в дальнейшем положим в основу понятия обобщенной силы, для которой введем обозначение Р.
Соответствующее данной обобщенной силе перемещение, на котором эта обобщенная сила совершает работу, называется обобщенным перемещением и будет обозначаться нами через ∆. На рис. 9.4 приведены примеры таких обобщенных перемещений. В первом случае (рис. 9.4, а) при действии на стержень пары сил S совершается работа A = S∆ и, следовательно, обобщенным перемещением здесь является удлинение ∆ стержня. Во втором случае (рис. 9.4,б) происходит взаимный поворот стержней на угол ψ, который может рассматриваться как обобщенное перемещение для обобщенной силы в виде группы моментов М. При этом совершается работа A = М ψ.
Рис.9.4
Наряду с действительными перемещениями, т.е. перемещениями, вызванными каким-либо конкретным силовым воздействием, будем рассматривать и возможные перемещения. Под возможным перемещением будем понимать малое перемещение, не зависящее от заданных внешних воздей-

ствий и удовлетворяющее имеющимся кинематическим связям. Даже для простейшей системы в виде простой балки (рис. 9.5) можно предложить сколь угодно большое число возможных перемещений.
Рис.9.5
С учетом введенных понятий возможная работа внешних сил определяется как работа заданных сил на возможных перемещениях
|
n |
|
|
|
A Pi zi , |
|
(9.26) |
|
i 1 |
|
|
где P i – |
обобщенные силы; |
|
|
zi – |
обобщенные перемещения, а |
суммирование |
понимается в |
|
алгебраическом смысле. |
|
|
По аналогии с этим можно ввести понятие возможной работы |
внутренних сил |
|
|
|
m |
|
|
|
Aвн Siei |
, |
(9.27) |
i 1
где Si – обобщенные внутренние усилия;
ei – соответствующие обобщенные деформации.
Знак «минус» в (9.27) указывает на то, что внутренние усилия совершают работу, противоположную работе внешних сил.
Теперь один из основных принципов механики – принцип возможных перемещений – может быть сформулирован в следующей форме:
n |
i |
|
m |
i i |
|
|
i |
|
|
0 . |
(9.28) |
Pz |
|
|
S e |
i 1 |
|
|
i 1 |
|
|
|
Таким образом, в силу принципа возможных перемещений для любой системы, находящейся в равновесии, сумма работ внешних и внутренних сил на любом перемещении должна быть равна нулю. С помощью принципа возможных перемещений может быть доказано свойство двойственности статических и геометрических уравнений, установленное ранее для статически определимых систем. Теперь покажем, что свойство остается справедливым и в общей теории расчета стержневых систем. Действительно, пусть рассматривается произвольная стержневая система, в которой








