8.4.Расчет многопролетных балок
1.Балка постоянного сечения (постоянный предельный момент). Определим предельную нагрузку на балку, изображенную на рис. 8.9,а.
Рис. 8.9
Подсчитываем предельную нагрузку для каждого пролета:
|
|
|
|
|
|
|
4 |
|
o |
|
1 |
|
o |
P1 l1 |
|
|
1 M o ; |
M |
н |
2 |
Mв |
M o |
P |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
l |
|
|
|
|
4 |
|
|
н |
2 |
в |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
ql2 |
M o M o ; q |
8 Mнo Mвo |
. |
|
|
|
|
|
8 |
|
|
н |
в |
пр |
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P2 |
l3 |
M o |
M o ; |
P |
4 Mнo Mвo |
. |
|
|
|
|
4 |
н |
|
в |
2 |
|
|
|
|
|
l3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P l |
M 0; |
P Mв0 . |
|
|
|
|
|
|
|
|
|
3 4 |
|
в |
3 |
|
|
l4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Предельная нагрузка на балку не должна превышать вычисленных для каждого пролета величин.
2. Балкапеременногосечения. (Предельныемоментыпролетовразличны.) Определим предельную нагрузку на балку (рис.8.10,а). Предельные
моменты пролетов показаны пунктиром на рис. 8.10,б.
Рис. 8.10
Pl |
|
|
o |
o |
; |
|
|
|
1 1 |
M1н M1в |
|
|
|
4 |
|
|
|
|
|
|
|
|
ql |
2 |
|
|
|
o |
|
|
o |
; |
|
M2oн M1в M3в |
8 |
|
|
|
|
2 |
|
|
P2ab |
|
o |
|
o |
|
|
|
|
|
|
M3н |
M |
36 |
|
; |
|
l3 |
|
|
P3l4 |
M4oн |
1 M |
3oв. |
|
|
4 |
|
|
|
|
|
2 |
|
|
|
|
Если загружение балки однопараметрическое, т.е.
P1 P; q2l2 P; P2 P; P3 P;
то предельной будет меньшая из нагрузок:
P 4 M1oн M1oв / l1; |
|
|
|
P 8 |
M o |
M1oв M3oв |
|
/ l |
; |
|
2н |
2 |
|
2 |
|
|
|
|
|
|
|
o |
|
o |
/ l3; |
P ab M3н |
M3в |
P 4 M4oн |
1 M3oв |
/ l4. |
|
|
2 |
|
|
3. Найти предельную нагрузку для симметричной относительно нейтральной оси трехпролетной балки (рис.8.11,а). Р1 Р; q28 2Р; Р2 5Р.
212
Решение.
Рис. 8.11
Р |
6 |
0 |
|
q 82 |
|
|
0 |
|
2М0 |
М0 |
0 |
|
1 |
|
1,5М |
; |
2 |
2М |
|
|
|
|
3,5М |
. |
4 |
|
|
2 |
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
Р2 4 |
3М0 |
1 |
2М0 4М0. |
|
|
|
|
|
|
2 |
|
|
|
|
4 |
|
|
|
|
|
|
|
|
1)Р М0.
2)2Р 3,5М0; Р 1,75М0.
3)5Р 4М0 , Р 54 М0.
Итак, Рпр 54 М0 (кН).
8.5. Реализация статического метода для рам
Положим, что в раме имеется достаточное количество точек, в которых могут одновременно образоваться пластические шарниры. Ввиду наличия пластических шарниров конструкция является статически определимой и ее прочность можно исследовать с помощью обычных линейных уравнений равновесия.
Пластические шарниры могут возникать в сечениях, примыкающих к узлам и местам защемления, а также в точках приложения сосредоточенных сил.
Уравнения равновесия можно подразделить на три группы: |
|
1. Уравнения равновесия узлов |
|
а) M1 M2 или |
M1 M2 0 |
|
б) M2 M1 M3 0 , т.е. в виде: |
|
|
q |
|
|
Mik 0 , |
(A) |
k 1
где q – количество сходящихся в i-й узел стержней.
Рис. 8.12
2. Уравнения проекций внешних и внутренних сил на горизонтальную ось (для рам):
m |
|
|
Six Qtk ( x) 0 , |
(B) |
i t |
k 1 |
|
где t – номер яруса рамы;
– количество стоек на этаже; m – количество этажей.
Здесь поперечные силы Qtk также можно выразить через концевые моменты стоек.
Рис. 8.13
3. Уравнения равновесия ригелей (балок).
Fky 0. |
n |
|
Pti( y) Qti( y) 0, |
(C) |
|
i 1 |
|
где n – номер нагрузки на ригель.
8.6. Пример решения задачи в статической формулировке
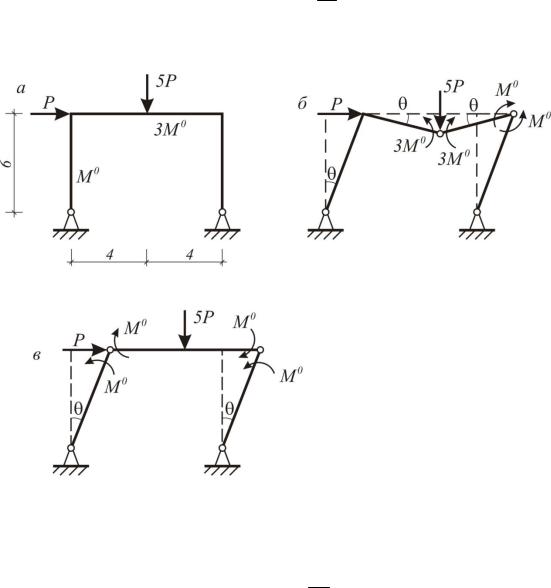
Определить параметр предельной нагрузки и распределение изгибающих моментовприпластическомразрушениидляпортальнойрамы(рис. 8.14,а).
Рис. 8.14
Дано:
M01 10 кН м
M02 3,375M01 33,75 кН м
Решение. Составим задачу линейного программирования: Найти max P при удовлетворении условий прочности:
|
M1 |
|
|
|
M0 , |
(1,8) * |
|
|
|
M2 |
|
|
|
M0 , |
(2,9) |
|
|
|
|
M3 |
|
|
|
3,375M0 , |
(3,10) |
|
|
|
|
|
M4 |
|
|
|
3,375M0 , |
(4,11) |
|
|
|
|
|
M5 |
|
|
|
3,375M0 , |
(5,12) |
|
|
|
|
|
M6 |
|
|
|
3,375M0 , |
(6,13) |
|
|
|
|
|
M7 |
|
|
|
M0 . |
(7,14) |
|
|
|
|
и выполнении уравнений равновесия:
а) узлов M2 M3 0; (15)
Рис. 8.15
* В скобках указаны номера ограничений задачи линейного программирования.
M4 M5 0; (16)
Рис. 8.16
M6 M7 0; (17)
Рис. 8.17 |
|
|
|
|
|
|
|
|
|
|
б) уравнений проекций на горизон- |
|
|
тальную ось |
|
|
|
|
|
|
|
|
|
|
P Q1 Q2 |
0; |
|
|
|
|
|
|
|
или |
M2 |
M1 |
M7 |
|
|
|
|
|
|
P |
h |
|
|
0; |
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
или, окончательно: |
|
|
|
|
|
|
|
|
4P M1 |
M2 M7 0.(18) |
|
|
|
|
Рис. 8.18 |
|
в) Уравнение равновесия ригеля |
|
|
|
|
или |
|
|
|
|
Fky 0 ; Q1y Q2 y 5P , |
|
|
|
|
M3 M4 |
|
|
M5 M6 |
|
|
|
|
|
|
|
|
|
|
5P . |
|
|
|
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
Это уравнение можно переписать в виде:
M3 M4 M5 M6 15P 0 . (19)
Рис. 8.19
Симплекс-таблица примет вид
|
Р |
М1 |
М2 |
М3 |
М4 |
М5 |
М6 |
М7 |
|
1 |
|
1 |
|
|
|
|
|
|
10 |
2 |
|
|
1 |
|
|
|
|
|
10 |
3 |
|
|
|
1 |
|
|
|
|
33,75 |
4 |
|
|
|
|
1 |
|
|
|
33,75 |
5 |
|
|
|
|
|
1 |
|
|
33,75 |
6 |
|
|
|
|
|
|
1 |
|
33,75 |
7 |
|
|
|
|
|
|
|
1 |
10 |
8 |
|
-1 |
|
|
|
|
|
|
10 |
9 |
|
|
-1 |
|
|
|
|
|
10 |
|
|
|
|
|
216 |
|
|
|
|
10 |
|
|
|
-1 |
|
|
|
|
33,75 |
11 |
|
|
|
|
-1 |
|
|
|
33,75 |
12 |
|
|
|
|
|
-1 |
|
|
33,75 |
13 |
|
|
|
|
|
|
-1 |
|
33,75 |
14 |
|
|
|
|
|
|
|
-1 |
10 |
15 |
|
|
-1 |
-1 |
|
|
|
|
=0 |
16 |
|
|
|
|
-1 |
-1 |
|
|
=0 |
17 |
|
|
|
|
|
|
-1 |
-1 |
=0 |
18 |
-4 |
1 |
1 |
|
|
|
|
1 |
=0 |
19 |
-15 |
|
|
1 |
1 |
-1 |
-1 |
|
=0 |
20 |
1 |
|
|
|
|
|
|
|
max |
21 |
5,128 |
+10 |
+0,51 |
-0,51 |
+33,75 |
-33,75 |
-10,0 |
+10,0 |
|
Решение задачи линейного программирования приведено в последней строке таблицы. Эпюра моментов в предельном состоянии показана на рис.8.14,б.
8.7. Предельное состояние рам.
Определение предельной нагрузки кинематическим способом
Рассмотрим задачу определения предельной нагрузки для рамы, показанной на рис. 8.20.
Рис. 8.20
Поперечное сечение всех элементов – одинаковое. Для отыскания Рпр воспользуемся кинематическим методом. Рассмотрим несколько вариантов разрушения – превращения рамы в механизм.
Рис. 8.21
Рис. 8.22
Рис. 8.23
а) Пластические шарниры образуются в узлах и сечениях около заделок (рис.8.21).
2P (1,5l ) 4M o 0;
P1 4M3l o .
б) Балочный механизм разрушения ригеля
(рис.8.22).
P |
|
1 |
4M o 0. |
2 |
|
|
|
P |
8M o |
. |
|
|
|
|
|
|
|
2 |
l |
|
|
|
|
|
|
в) Комбинированный механизм разруше-
ния (рис. 8.23).
2P 1,5l P l 6M o 0.2
P 12M o .
3 7l
Минимальное значения P P1 4M3l o . Та-
ким образом действительный механизм разрушения – первый.
Проверим правильность решения. Согласно статической теореме при Р1 должны выполняться уравнения равновесия.
M A 0 2P 32 l P 2l M o 2 VB l 0;
MCпр 0 P 2l VB l HB 32 l 0;
M Dправ 0 HB 1,5l 2M o 0.
Решив уравнения, получим
P 4M3l o ,
т.е. кинематически возможное состояние является и статически возможным, а, значит, этот механизм разрушения является действительным и
Pпр 4M3l o .
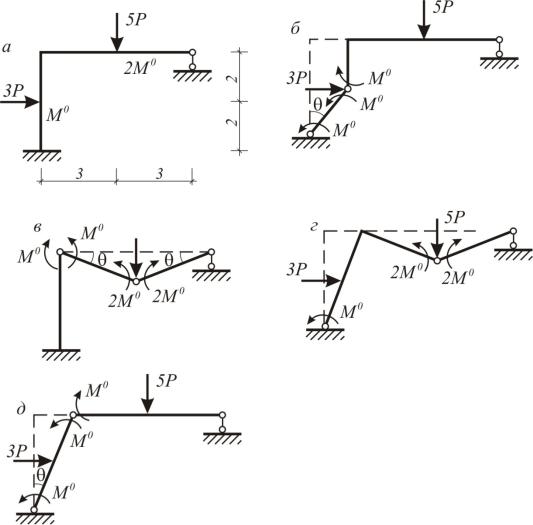
Пример №2. Рассчитать раму методом предельного равновесия. Определить предельную нагрузку на раму (рис.8.24).
При формировании механизмов разрушения для двухстержневого узла пластический шарнир располагаем в более слабом стержне.
Рис. 8.24
Для механизма (рис.8.24,в):
3Р 2 2М0 ,
Р1 М30 .
Для механизма (рис.8.24,г):
3Р 2 5Р 3 5М0 ,
Р3 5М0 . 21
Для механизма, изображенного на рис.8.24,д: 3Р 2 2М0 ,
Р4 М30 .
Минимальное значение критической нагрузки соответствует механизму, показанному на рис.8.24,д.
Рпр Р3 215 М0.
Пример №3. Определить предельную нагрузку на раму (рис.8.25,а).
Рис. 8.25
Для рис.8.25,б:
Р 6 5Р 4 7М0 .
Р1 267 М0 .
Для рис.8.25,в:
Р6 2М0 , Р2 13 М0 .