ное перемещение массы Y1(t) будет складываться из переносного перемещения (t) и относительного перемещения y(t) :
Y (t) (t) y(t) , |
(7.61) |
где относительное перемещение можно записать в виде: |
|
y(t) 11 Ф. |
(7.62) |
Сила инерции, действующая на движущуюся массу, равна: |
|
Ф mY (t). |
(7.63) |
Следовательно, уравнение перемещений примет вид: |
|
Y (t) (t) (mY (t)) . |
(7.64) |
11 |
|
Поделив это равенство на m 11 , придем к виду: |
|
Y (t) 2Y (t) 2(t) . |
(7.65) |
Это и есть дифференциальное уравнение движения массы вследствие кинематического воздействия. С учетом (7.61) уравнение движения можно переписать в виде:
Упругая система с n степенями свободы реагирует на сейсмическое воздействие каждой составляющей своего спектра собственных колебаний vk (k 1,2,...,n) . Поэтому решение задачи определения динамических
перемещений и инерционных сил можно провести с помощью разложения искомого движения по собственным формам колебаний. При этом вектор прогибов y(t) представим как сумму произведений (рис.7.40):
|
n |
|
|
y qk vk . |
(7.67) |
|
k 1 |
|
|
Здесь qk – обобщенная координата, определяемая из |
решения диф- |
ференциального уравнения: |
Qk (t) . |
|
q |
2q |
(7.68) |
k |
k |
Mk |
|
|
|
|
В уравнении (7.68): Qk – обобщенная сила: |
|
n |
|
n |
(7.69) |
Qk Фivik mivik , |
i 1 |
|
i 1 |
|
Мk – обобщенная масса k-й формы: |
n |
|
|
|
|
|
Mk |
mivik2 . |
(7.70) |
i 1
Рис. 7.40
Таким образом, дифференциальное уравнение для вычисления обобщенной координаты, соответствующей k-й собственной форме колебаний, примет вид:
n
mivik
qk 2qk i 1 . (7.71)
n
mivik2
i 1
Вектор форм собственных колебаний (амплитудных коэффициентов) v находитсяизрешениязадачинасобственныезначения(см. алгоритм(7.41)-(7.47)).
При заданном сейсмическом воздействии (t) уравнение (7.71) в соче-
тании с (7.67) дает возможность определить динамические перемещения точек системы. Динамические силы, соответствующие k-й форме колебаний можно найти с помощью соотношения:
|
|
s1k |
|
m1v1k |
|
|
|
s |
|
|
|
m v |
|
|
|
|
|
|
2k |
|
|
2 |
2k |
|
|
|
|
: |
|
2 |
|
: |
|
|
|
|
|
|
|
Sк s |
|
qк к |
m v |
. |
(7.72) |
|
|
|
ik |
|
|
i |
ik |
|
|
|
|
: |
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
snk |
|
mnvnk |
|
Сейсмическое воздействие обычно носит ярко выраженный нестационарный характер. На рис.7.41 приведена зависимость ускорения движения грунта при землетрясении от времени – акселерограмма землетрясения.
202
Рис. 7.41
Поэтому сейсмический расчет здания или сооружения можно выполнить приближенно на основе расчета по нескольким акселерограммам, характерным для данного района.
7.8. Динамические воздействия на здания и персонал. Защита от динамических воздействий
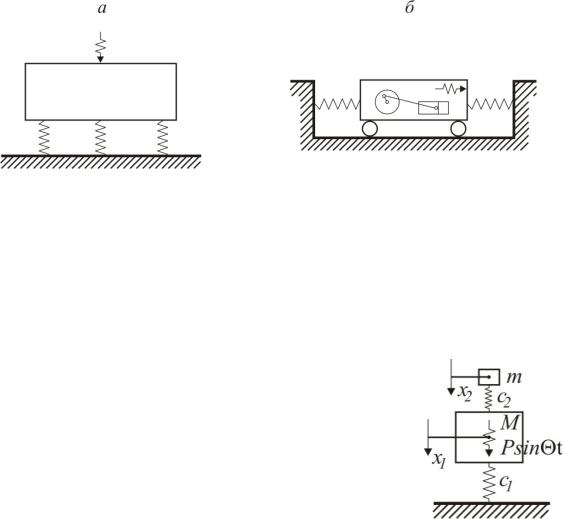
При вибрационном воздействии в элементах конструкции возникают знакопеременные напряжения, которые, в свою очередь, приводят к накоплению повреждений в материале в виде трещин и в итоге к разрушению. Кроме того, вибрационные воздействия, не вызывая разрушения объекта, могут приводить к нарушению их нормального функционирования. Например, вибрации оснований приводят к снижению точности и чистоты обработки деталей на станках, существенно влияют на точность показаний приборов (электронный микроскоп, точные весы и т.п.). Нарушение функционирования объекта, не связанного с разрушением или другими необратимыми изменениями, называется отказом.
Таким образом, колебательные воздействия могут вызывать как разрушения конструкции, так и отказы машин, приборов и аппаратов.
Способность конструкции не разрушаться при механических колебаниях называется вибропрочностью, а способность нормально функционировать – виброустойчивостью. Цель виброзащиты строительных объектов – обеспечение их вибропрочности и виброустойчивости.
Особенностью вибрационного воздействия является и отрицательное влияние на здоровье людей, находящихся вблизи источника вибрации или непосредственно в контакте с ним. Болезненные ощущения от вибрации проявляются уже при ускорениях, составляющих 5 % от ускорения силы
тяжести, т.е. при y 0,5 м/с2 . Чувствительность к вибрациям зависит как
от амплитуд, так и от частот. При больших частотах амплитуды существенно ограничиваются нормами. Особенно вредны вибрации с
203
Рис. 7.42
частотами, близкими к частотам собственных колебаний частей тела человека, большинство из которых находится в области 6 30 Гц.
Мероприятия, рекомендуемые при проектировании и реконструкции
При проектировании машин в первую очередь стремятся уравновесить их вращающиеся части, которые создают как вертикальные, так и горизонтальные нагрузки. Для плоских перекрытий зданий наибольшую опасность представляют вертикальные колебания. Задача проектировщиков зданий свести к минимуму динамические воздействия путем имеющихся в их
распоряжении средств. Одним из таких приемов является соответствующая расстановка станков на предприятии. Станки рекомендуется расставлять ближе к опорам перекрытий. Их вращение должно быть ориентировано в направлении большей жесткости здания, как правило, в продольном направлении (рис.7.42).
Фундаменты под компрессоры и другие ударные механизмы желательно располагать на первом этаже на отдельных фундаментах, независимых от фундаментов здания.
Реконструкция зданий, как правило, связана с увеличением числа оборотов двигателей станков и механизмов. Чтобы избежать возможного появления резонанса, необходимо увеличивать низшую частоту колебаний конструкции. Для этого нужно увеличивать жесткость конструкции
(mx cx 0; x mc x 0; x 2 x 0; 2 mc .) .
Повышения жесткости можно добиться путем:
а) устройства вутов в железобетонных конструкциях (рис.7.43,а), б) установки дополнительных связей (рис. 7.43,б,в); в) устройства дополнительных опор (рис.7.43,г).
Рис. 7.43
Виброизоляция
Виброизоляцией называется способ уменьшения колебаний какой-либо механической системы, основанный на значительном ослаблении ее связей с другими системами. Между источником колебаний и защищаемым объектом вставляется виброизолирующее устройство (рис.7.44,а – вертикальная виброизоляция, рис.7.44,б – горизонтальная виброизоляция).
Рис. 7.44
Динамический гаситель колебаний
Динамическим гасителем колебаний называют устройство, в котором возникает сила инерции, уменьшающая уровень колебаний защищаемой конструкции. При этом энергия колебаний передается гасителю, который настроен на частоту колебаний системы и благодаря этому колеблется с повышенной амплитудой.
Пусть основная колебательная система (защищаемая конструкция) имеет массу М и жесткость с1 (рис.7.45). На защищаемую конструкцию, находящуюся под действием возмущающей силы Psin t , установлен динамический гаситель колебаний, имеющий массу m и жесткостьc2 .
Уравнения движения этой механической системы имеют вид:
Mx1 (c1 c2 )x1 c2 x2 |
Psin t; |
mx2 c2 (x2 x1) 0. |
|
|
При установившихся вынужденных колебаниях: x1 A1 sin t; x2 A2 sin t.
Подставив координаты в уравнение движения, получим:
|
|
2 |
|
|
|
|
M |
A1 |
(c1 c2 )A1 c2 A2 |
P, |
|
|
|
m 2 A |
c (A A ) 0, |
|
|
|
|
|
|
2 |
2 2 1 |
|
|
|
|
Рис. 7.45
(7.73)
(7.74)
(7.75)
или
|
|
A1(c1 c2 |
|
2 |
|
|
|
|
|
|
M |
) A2c2 |
P, |
|
|
|
|
(7.76) |
|
|
A c A (c m 2 ) 0. |
|
|
|
|
|
|
|
1 2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
Откуда находим формулы для амплитуд: |
|
|
|
|
|
|
|
A1 |
|
|
|
P(c m 2 ) |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
; |
|
|
|
(c |
c |
M 2 )(c |
m 2 ) c2 |
|
|
|
1 |
2 |
|
|
2 |
|
2 |
|
|
(7.77) |
|
|
|
|
|
|
|
P c2 |
|
|
|
|
|
|
A2 |
|
|
|
|
|
|
. |
|
|
|
(c |
c |
M 2 )(c |
m 2 ) c2 |
|
|
|
1 |
2 |
|
|
2 |
|
2 |
|
|
|
При |
c m 2 |
A 0. |
|
|
|
|
|
|
|
(7.78)-(7.79) |
|
2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
Т.е. при соответствующем подборе жесткости (и массы) гасителя можно добиться, что основная масса будет практически оставаться в покое.
Основной недостаток динамического гасителя колебаний состоит в том, что он хорошо работает только при стационарных колебаниях, когда
cm2 .
Если это условие не выполняется, то эффективность работы гасителя существенно снижается. Силы инерции, действующие на массы в идеальном работающем гасителе, равны:
|
2 |
A1 |
0; |
|
|
J1 M |
|
(7.80) |
J |
m 2 A |
P. |
2 |
|
2 |
|
|
|
|
|
|
|
Т.е. внешняя сила уравновешивается силой инерции массы гасителя.
8. РАСЧЕТ БАЛОК И РАМ НА ОСНОВЕ ТЕОРИИ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ
8.1. Пластическое состояние сечения балки
Диаграмму зависимости напряжения от деформаций достаточно пластичных материалов (например строительных сталей) можно представить следующим графиком (рис.8.1).
Рис. 8.1
Здесь участок ОА диаграммы отвечает I, упругой, стадии деформирования, где Е . Горизонтальный участок АВ приведенной диаграммы описывает II, пластическую, стадию дефор-
мирования, где Т ; Е 0.
Кривая ВС отвечает III стадии – стадии упрочнения. Она завершается разрушением образца при напряжении вр , называемом
временным сопротивлением.
Для проведения практических расчетов реальную диаграмму удобно заменить упрощенной диаграммой Прандтля (рис.8.2), отвечающей идеальному упругопластическому материалу.
Если при этом учесть, что величины пластических деформаций во много раз превышают величины упругих деформаций, то можно даже перейти к диаграмме жестко-пластического материала (рис.8.3).
В 1938 году А.А. Гвоздев, основываясь на упрощенной диаграмме работы материала, предложил особый метод опреде-
ления предельной несущей способности. Идея метода состоит в том, что конструкция рассматривается в момент, непосредственно предшествующий ее разрушению, когда еще выполняются условия равновесия для внутренних и внешних сил, достигших предельных значений. Отсюда произошло и название метода – «метод предельного равновесия».
Для систем, работающих преимущественно на изгиб (балок, рам), разрушение определяется в основном величиной изгибающих моментов.
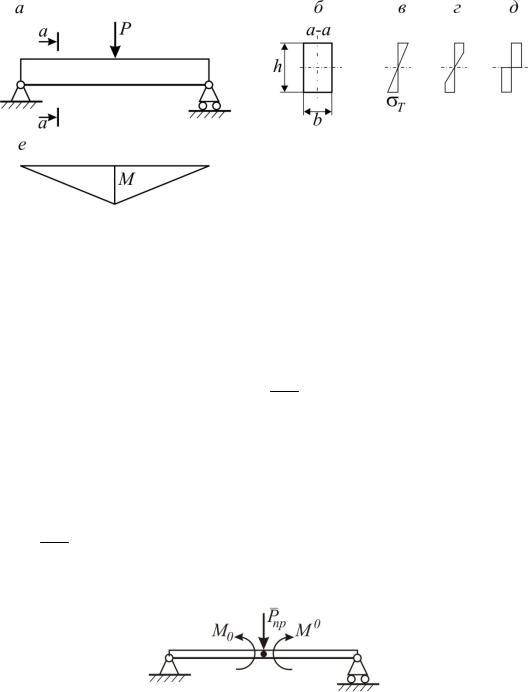
Рассмотрим возрастающее нагружение балки (рис. 8.4,в,г,д).
Рис. 8.4
При работе в упругой стадии (рис. 8.4,в) момент внутренних сил равен:
M 2 12 b h2 32 h2 bh62 Wуп,
где
Wуп bh62 .
При работе в пластической стадии момент внутренних сил (рис.8.4,д) равен:
MT M 0 T b h2 12 h2 2 T bh42 T Wпл .
где Wпл bh42 .
Достижение состояния полной пластичности сечения называется появлением пластического шарнира (рис.8.4,д, 8.5).
Рис. 8.5
Рис. 8.6
Пластический шарнир отличается от идеального шарнира тем, что в нем действует изгибающий момент постоянной ве-
личины M 0 . После появления одного пластического шарнира в статически определимой балке балка становится геометрически изменяемой, т.е. происходит ее разрушение. После появления пластического шарнира в статически неопределимой балке (рис. 8.6,а) еще не произойдет разрушения.
Предельное состояние наступит, когда образуются два пластических шарнира (рис.8.6,б) и балка превратится в механизм. Будем полагать, что шарниры в балках образуются одновременно. Условия прочности сечения балок можно записать в виде
где К – номер балки,
i – номер сечения балки.
Это условие означает, что действующий изгибающий момент меньше или равен пластическому моменту сечения. M K0 – несущая способность сечения К балки.
8.2. Основные теоремы метода предельного равновесия
Системы, находящиеся в состоянии предельного равновесия обладают экстремальными свойствами, характеризуемыми следующими теоремами.
Статическая теорема: нагрузка, соответствующая статически возможному состоянию системы, меньше, чем предельная нагрузка.
Другими словами, наибольшую величину нагрузки для статически неопределимой системы можно определить, перебирая различные варианты распределения внутренних усилий, зависящие от расположения пластических шарниров.
Эта теорема дает нижнюю оценку предельной нагрузки.
Задачу определения предельной нагрузки можно представить в виде
задачи линейного программирования: |
max P |
найти |
при выполнении уравнений равновесия: |
|
fi (Mik Mk0 ) 0 |
и ограничений по прочности: |
|
Mik |
|
Mk0 , |
|
|
где Р – искомый параметр предельной нагрузки при однопараметрическом загружении;

M K0 – предельный момент сопротивления k-го элемента;
Mik – момент в i-м сечении k-го элемента.
Кинематическая теорема: нагрузка, соответствующая кинематическивозможномусостояниюсистемы, больше, чемпредельнаянагрузка.
Эта теорема дает верхнюю оценку предельной нагрузки.
Расчет предельной нагрузки по кинематической теореме имеет вид: min P
при Pi i Mk0 k 0 ,
k
Mik Mk0 .
8.3.Расчет балки на основе статического
икинематического критериев
Определим предельную нагрузку для балки (рис.8.7), загруженную силой Р в середине пролета.
Для превращения балки в механизм необходимо образование двух пластических шарниров. Первый шарнир возникает у защем-
Рис. 8.7 ления А. При дальнейшем возрастании нагрузки образуется шарнир в середине пролета – под силой Р. Определим Рпр статическим
способом. Из рис. 8.8,б, в
Мб 1,5М0 или Pl4 1,5M 0 ,
откуда Рпр 6Мl 0 .
Теперь воспользуемся кинематическим способом (рис. 8.8,а).
Составим уравнение принципа возможных перемещений:
P |
l |
Mпр 2Mпр 0. |
|
|
|
2 |
|
|
|
|
Из этого уравнения определяем: |
|
|
|
P |
l |
3M 0. |
|
|
|
|
|
|
|
2 |
|
|
|
|
P 6M 0 . |
Рис. 8.8 |
|
|
пр |
l |
|
|
|
|
|
|