
2545
.pdf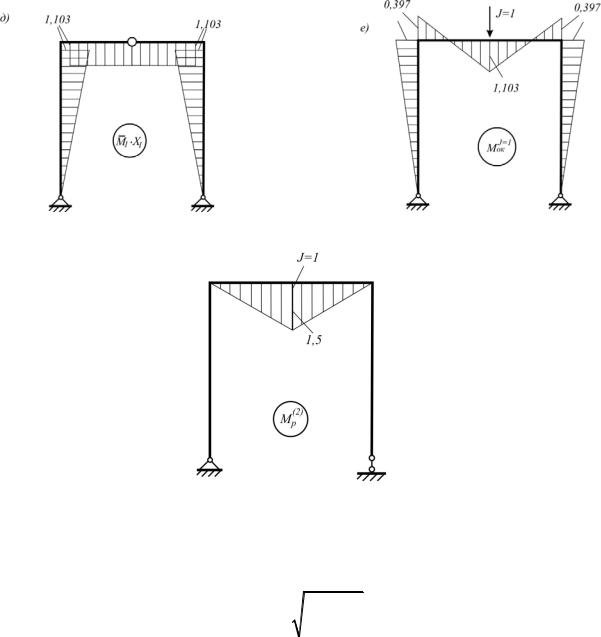
|
|
1 |
|
|
2 1 |
1 4 2 |
1 1 6 1 |
1 |
|
|
17 |
. |
|
|
|
|
|
||||||||
11 |
|
EI |
|
2 |
3 |
|
2 |
|
3EI |
|||
|
|
|
|
|
|
|
||||||
|
|
1 |
|
2 |
|
1 1,5 |
4 |
21 |
1 1,5 31 1 |
|
6,25 |
|
25 |
. |
||||||||||||
|
|
|
|
|||||||||||||||||||||||
1p |
|
EI |
|
|
2 |
|
|
|
|
|
3 |
|
2 |
|
2 |
EI |
|
4EI |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
X1 |
|
|
1p |
|
|
25 |
/ |
17 |
|
25 3 |
1,103 . |
|
|
|
|||||||
|
|
|
|
|
|
11 |
|
|
4EI |
|
3EI |
17 4 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
aa |
|
|
1 |
|
2 |
3 2 1,1031,5 0,397 1,5 1,357 . |
|||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
2EI |
|
6 |
|
|
|
|
|
|
|
|
|
|
EI |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ж)
Рис. 7.21
Получаем, что частота вертикальных колебаний равна:
|
|
1 |
. |
m |
1,357 |
||
|
|
EI |
|
181

Пример № 4. Определить частоту собственных горизонтальных колебаний рамы (рис. 7.22,а).
Рис. 7.22
Перемножив кососимметричную эпюру МР (см. рис.7.22,а) на симметричную М1 (см. рис.7.22,б), получим:
|
|
|
|
|
|
1p |
|
0. |
|
|
|
|
|
|
|
|
|
||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X1 0. |
|
|
|
|
|
|
|
|
|
|||
Тогда МР =Мок и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
aa 2 |
1 |
|
1 |
2 4 |
2 |
2 |
1 |
2 3 |
|
2 |
2 |
|
1 |
|
|
14,667 |
. |
||
|
|
2 |
3 |
2 |
3 |
2 |
|
EI |
|||||||||||
|
|||||||||||||||||||
|
EI |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
14,667 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
EI |
|
|
|
|
|
|
|
|
|
|
7.5. Колебания систем с конечным числом степеней свободы
7.5.1.Дифференциальные уравнения движения
На рис.7.23 показана система с n степенями свободы, т.к. в данном случае каждая точечная масса здесь обладает одной степенью свободы.
182

Рис. 7.23
Согласно принципу суперпозиции перемещение i-й массы можно определить следующим образом:
yi i1J1 i2 J2 ... |
ii Ji ... |
in Jn ip P(t) , |
(7.27) |
i 1,2,...,n .
Здесь ij – единичное перемещение i-й массы по своему направлению от j-й силы инерции, равной единице; ip – единичное перемещение от
внешней нагрузки, равной единице.
Данное уравнение можно переписать в виде:
i1J1 i2 J2 ... ij Ji ... in Jn yi ip P(t) 0. |
(7.28) |
Эти уравнения можно рассматривать как уравнения метода сил с |
|
неизвестными силами инерции. Как известно, |
|
Ji mi yi , |
(7.29) |
ip (t) ip P(t). |
(7.30) |
Подставив (7.22) в (7.21), получим: |
|
i1m1 y1 i2m2 y2. .... iimi yi ... inmn yn yi ip (t) 0 , |
(7.31) |
i 1,2,...,n .
Мы получили систему дифференциальных уравнений динамического равновесия механической системы с n степенями свободы.
7.5.2. Свободные колебания системы с n степенями свободы
Если возмущающие нагрузки равны нулю, то ip (t) 0 . Уравнения движения в этом случае примут вид
ijm1 y1 i2m2 y2 ... iimi y j ... inmn yn yi 0 ; |
(7.32) |
i 1,2,...,n .
183
Для решения этой системы уравнений применим способ разложения по собственным формам колебаний. Представим, что любое перемещение yi (t) может быть записано в виде суммы n функций
n |
|
yi (t) yik , |
(7.33) |
k 1
причем каждая из функций yik (t) , в свою очередь, определяется выражением
yik (t) Yik Фk (t) . |
(7.34) |
Здесь Yik – амплитудный коэффициент;
Фk – неизвестная пока функция времени, соответствующая k-й собственной форме колебаний.
Произвольной k-й собственной форме соответствует решение:
y1 Y1k Фk (t), |
y2 Y2k Фk (t),..., |
yn Ynk Фk (t) . |
(7.35) |
Подставляя эти решения в систему уравнения (А), для каждой k-й формы колебаний будем иметь
(i1m1Y1k i2m2Y2k ... inmnYnk )Фk (t) YikФk (t) 0 . (7.36)
Разделяя переменные, придем к уравнению вида
|
|
|
(t) |
|
|
|
|
Yik |
|
|
|
|
|
Фk |
|
|
|
|
|
|
. |
(7.37) |
|||
|
(t) |
|
m Y |
|
m Y |
... |
m Y |
|||||
|
Ф |
k |
|
|
|
|||||||
|
|
|
|
|
i1 1 1k |
|
i2 2 2k |
|
in n nk |
|
|
|
Правая часть этого уравнения – величина постоянная. Обозначим ее через 2k , тогда и левая часть равна 2k , т.е.
|
2 |
(7.38) |
Фk (t) k Ф(t) 0 , |
||
( |
m Y |
|
m Y |
... |
m Y |
) 2 |
Y |
0. |
(7.39) |
||
|
i1 |
1 1k |
|
i2 2 2k |
|
|
in n nk |
k |
ik |
|
|
Уравнение (7.31) |
имеет известное решение: |
|
|
|
|
||||||
Фk Ak sin |
kt Bk cos |
kt Ck sin( kt k ) , |
(7.40) |
||||||||
которое показывает, что колебания происходят по гармоническому закону, а k – частота собственных колебаний k-й формы. Следовательно,
амплитудные коэффициенты Yik – это перемещение масс m1,m2 ,...,mn , которые определяют функции yik , соответствующие k-й собственной (глав-
ной) форме колебаний. При этом все точки системы совершают гармоническое колебание с одной и той же частотой, а отношение любых двух амплитудных коэффициентов остается постоянным.
184

Запишем уравнения (7.32) в виде: |
|
|
|
|
|
|
|
|||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
m1 11 |
Y1k m2 12Y2k |
... mn 1nYnk |
0; |
|
|
|||||||||
2 |
|
|||||||||||||
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
1 |
Y |
|
|
|
|
|
|
|
||
m Y |
22 |
|
... m |
|
Y |
0; |
|
|||||||
2 |
|
|||||||||||||
1 21 1k |
|
|
2 |
|
2k |
|
n |
2n nk |
|
|
(7.41) |
|||
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
........................................................................ |
|
|
||||||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
m1 n1Y1k |
m2 n2Y2k |
... mn nn |
|
Ynk |
0. |
|
||||||||
2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Это система линейных однородных алгебраических уравнений относительно амплитудных коэффициентов k-й формы собственных колебаний. Нетривиальное решение находим, приравнивая определитель этой системы нулю:
|
m1 11 |
k |
m2 12 ... |
mn 1n |
|
|
|||
|
|
|
|||||||
|
m1 21 |
m2 22 |
k ... |
mn 2n |
0 . |
(7.42) |
|||
|
..................................................... |
|
|
||||||
|
m1 n1 |
m2 n2 |
|
... mn nn k |
|
|
|||
Здесь число |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
k |
|
|
|
|
(7.43) |
||
|
|
2 |
|
|
|||||
|
|
|
|
|
k |
|
|
|
|
называется «собственное значение».
Раскрыв определитель, получим уравнение частот (или вековое уравнение) в виде:
n n 1 |
|
n 2 ... |
( 1)n |
n |
0 . |
(7.44) |
1 |
2 |
|
n 1 |
|
|
Это уравнение имеет n корней, каждый из которых соответствует частоте собственных колебаний. Затем на основе соотношения
k |
1/ k |
(7.45) |
определяем n частот собственных колебаний, т.е. спектр. Совокупность частот называется спектром и обладает упорядоченностью:
1 2 ... n . |
(7.46) |
Наименьшая частота спектра называется основной частотой, а все остальные – высшими.
185

Так как из однородной системы уравнений (7.33) нельзя определить абсолютные значения Yi , то вычисляются их относительные значения для
каждой частоты. Для этого один из амплитудных коэффициентов принимается равным 1, а остальные вычисляются из линейной системы ( n 1) уравнений.
Полученные векторы
|
|
k 1,Y |
,Y |
,...,Y |
T |
(7.47) |
Y |
||||||
|
|
2k |
3k |
nk |
|
|
называются собственными векторами.
После этого можно составить уравнение движения каждой i-й массы:
n |
|
|
||
yi (t) Yik (Ak sin kt Bk cos kt) , |
(7.48) |
|||
k 1 |
|
|
||
где постоянные интегрирования Ak |
и Bk определяются из 2n начальных |
|||
условий: |
|
|
||
yi |
|
t 0 |
yi (0); |
(7.49) |
|
||||
|
||||
yi |
|
|
yi (0). |
|
|
t 0 |
|
||
|
|
|||
Пример №1. Вычислить частоты свободных колебаний невесомой балки с двумя одинаковыми массами (рис.7.24,а), расположенными в третях пролета. Составить уравнения движения масс.
Рис. 7.24
Данная система – система с двумя степенями свободы. Канонические уравнения свободных колебаний:
(m1 11 )Y1k m2 12Y2k 0, . m1 21Y1k (m2 22 )Y2k 0.
186

Уравнение частот имеет вид:
D |
|
(m1 11 ) |
m2 12 |
|
=0. |
|||
|
|
|||||||
|
|
m |
21 |
(m |
22 |
) |
|
|
|
|
1 |
2 |
|
|
|
||
Вековое уравнение, полученное из этого определителя, имеет вид
2 (m1 11 m2 22 ) m1m2 ( 11 22 122 ) 0 .
Для решения этого уравнения построим эпюры от единичных инерционных сил, приложенных в направлении колебаний каждой массы (рис.7.24,б,в), и вычислим перемещения 11, 12 , 22. Перемножив единич-
ные эпюры, получим:
11 |
|
M M |
1dx |
4l3 |
|
|
|
||||||
|
EI1 |
|
. |
|
|||||||||
|
243EI |
||||||||||||
|
22 |
|
|
4l3 |
|
. |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||||
|
11 |
|
|
243EI |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
M M |
2 dx |
|
7l3 |
||||||
12 |
21 |
|
E1 |
I |
|
. |
|||||||
|
486EI |
||||||||||||
Подставив перемещения в вековое уравнение, получим:
|
|
|
|
1 m ( |
|
|
|
|
|
22 |
) |
( |
|
22 |
)2 42 |
|
|
||||||||||||||||||||||||||||||||
|
1,2 |
|
|
2 |
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
12 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
l |
3 1 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
2 |
0 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
EI 2 |
243 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
486 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
2 |
|
|
2 |
7 |
|
|
|
l |
3 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
243 |
|
486 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
2EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
30 |
|
|
|
|
|
l3 |
|
|
m; |
|
2 |
|
2 |
|
|
|
|
l3 |
|
m. |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
486 2EI |
|
|
|
|
|
|
|
|
|
|
486 2EI |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
5,69 |
|
|
|
EI |
; |
|
2 |
22,05 |
|
EI |
. |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
ml3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ml3 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Пусть колебания происходят с частотой 1 . Примем Y11 1. Тогда |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30 |
l3 |
|
|
|
|
|
|
|
|
4l3 |
|
|
|
7 |
|
|
|||||||||||||||
|
|
1 m1 11 |
|
|
|
486 |
|
|
m m |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
Y |
|
|
|
|
2EI |
|
243EI |
486 |
1. |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
21 |
|
|
|
m2 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
7l3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
486 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
486EI |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
187

Если колебания происходят с частотой 2 |
и Y12 1, то |
|||||||||||||
|
|
|
|
|
|
1 l3 |
|
4l3 |
||||||
|
|
2 m1 11 |
|
|
|
|
|
m m |
|
|
|
1. |
||
Y |
|
486 |
EI |
243EI |
|
|||||||||
|
|
|
|
|
|
|
|
|||||||
22 |
|
m |
|
|
|
|
|
m |
7l3 |
|
|
|
|
|
|
|
2 |
12 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
486EI |
|
|
||||
Собственные формы колебаний, соответствующие 1-й и 2-й частотам, показаны на рис. 7.25.
1-я главная форма колебаний
2-я главная форма колебаний
Рис. 7.25
Законы движения массы 1 и массы 2:
2
y1 Y1k Ak sin kt Bk cos kt
k1
Y11 A1 sin 1t B1 cos 1t Y12 A2 sin 2t B2 cos 2t ;
y2 Y21 A1 sin 1t B1 cos 1t Y22 (A2 sin 2t B2 cos 2t).
Подставив Yik и k в уравнения движения масс, получим:
y1 |
1 A1 sin(5,69t) B1 cos(5,69t) 1 A2 sin(22,05t) B2 cos(22,05t) ; |
||||||
y2 |
1 A1 sin(5,69t) B1 cos(5,69t) 1 A2 sin(22,05t) B2 cos(22,05t) ; |
||||||
y1 |
5,69A1 cos(5,69t) 5,69B1 sin(5,69t) 22,05A2 cos(22,05t) 22,05B2 sin(22,05t); |
||||||
y2 |
5,69A1 cos(5,69t) 5,69B1 sin(5,69t) 22,05A2 cos(22,05t) 22,05sin(22,05t). |
||||||
|
Примем следующие начальные условия движения: |
||||||
|
|
y1(0) 1, y2(0) |
0, |
||||
|
y |
0, y |
2(0) |
0, |
|
EJ |
1. |
|
|
|
|||||
|
1(0) |
|
|
|
ml3 |
||
|
|
|
|
|
|
||
188

Подставим начальные условия в уравнения движения:
1 B1 |
B2; |
|
0 B1 B2; |
|
|
|
||
0 5,69A 22,05A |
; |
|
1 |
2 |
|
0 5,69A |
22,05A |
. |
1 |
2 |
|
Решая систему, находим: |
|
|
B1 B2 0,5; |
|
|
A1 A2 0. |
|
|
Таким образом, при данных начальных условиях (рис.7.26) уравнения колебательного движения примут вид:
y1 0,5cos(5,69t) 0,5cos(22,05t), y2 0,5cos(5,69t) 0,5cos(22,05t).
Рис. 7.26
Таким образом, из уравнений свободных колебаний можно:
1)вычислить частоты собственных колебаний, соответствующие главным формам;
2)построить графики стоячих волн колебаний, соответствующие каждой частоте;
3)составить уравнения колебательного движения каждой массы, в зависимости от начальных условий.
7.5.3. Примеры расчета рам на свободные колебания
Пример №2. Определить частоты собственных колебаний рамы с двумя сосредоточенными массами (рис.7.27). l 4,5 м, h 3 м, m1 150 кг,
m2 100 кг, EI const, l / h 1,5; m1 / m2 1,5.
Рис. 7.27
189

Каждая масса здесь имеет 1 степень свободы, т.е. это система с двумя степенями свободы. Канонические уравнения колебаний:
m1 11 Y1k m2 12Y2k 0; m1 21Y1k m2 22 Y2k 0.
Уравнение частот имеет вид:
D m1 11
m1 21
Вековое уравнение:
2 m1 11 m2 22
Решение векового уравнения:
1,2 12 m1 11 m2 22
m2 12 |
|
0 . |
|
||
(m2 22 ) |
|
|
|
|
m1m2 11 22 122 0 .
m1 11 m2 22 |
2 |
2 |
|
(*) |
|
4m1m2 12 |
. |
||
|
|
|
|
|
Для определения корней векового уравнения надо вычислить перемещения 11, 12 , 22 от единичных инерционных воздействий, как от нагрузки
(рис.7.28).
Рис. 7.28
Т.к. рама статически и кинематически неопределима, для построения эпюр от J1 1и J2 1 решим задачу методом перемещений:
z (1) |
|
R1p (I ) |
|
3l /16 |
|
; |
|
||||||
|
|
|
|
|
l h |
|
|||||||
1 |
|
|
|
r11 |
|
|
3EI |
|
|
||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
R1p (II ) |
|
hl |
|
|
|
||||
z (2) |
|
|
|
|
3h /16 |
; |
|||||||
|
|
|
|
|
l h |
||||||||
1 |
|
|
|
r11 |
|
|
|
3EI |
|
||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
hl |
|
|||
M1 M z1(1) Z1(1) M J1 ;
M2 M z1(2) Z1(2) M J 2.
190
