
2545
.pdf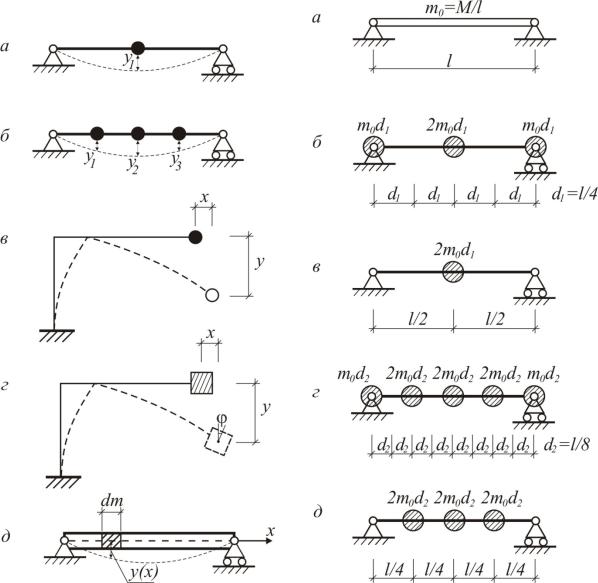
балку с распределенной массой можно привести к системе с одной (рис.7.7,б,в), тремя (рис. 7.7,г,д) и т.д. степенями свободы. Вопрос о количестве масс решается в каждом случае отдельно. От этого в некоторой степени зависит точность динамического расчета.
Рис. 7.6 |
Рис. 7.7 |
В дальнейшем будем рассматривать системы с конечным числом степеней свободы.
171

7.4. Уравнение движения (динамического равновесия) для системы с одной степенью свободы
Составим уравнения динамического равновесия массы на основе принципа Даламбера. Силу инерции, действующую на массу, обозначим
J my . |
(7.1) |
Составим выражение, определяющее перемещение сосредоточенной массы на балке, изображенной на рис.7.8:
y 1p (t) 11J . |
(7.2) |
Здесь 1p – перемещение точки 1 по направлению рассматриваемого перемещения от силы P(t) ;
11 – единичное перемещение точки 1 от силы J 1.
Рис. 7.8
Подставив (7.1) в (7.2), получим: |
|
|
|
|
|
|
11my y 1p (t) . |
|
(7.3) |
||
Введем обозначение |
|
|
|
|
|
|
2 |
1 |
|
|
|
|
|
|
. |
|
(7.4) |
|
m |
|
|||
|
|
11 |
|
|
|
Подставив (7.4) в (7.3), получим: |
|
|
|
|
|
|
y 2 y 2 |
(t) 2 |
Р(t) . |
(7.5) |
|
|
1 p |
|
1p |
|
|
При правой части, равной нулю, имеем случай свободных колебаний |
|||||
y 2 y 0 |
|
|
|
|
(7.6) |
с решением |
|
|
|
|
|
|
y Asin( t ) . |
|
(7.7) |
||
Здесь A – |
амплитуда колебаний; |
|
|
|
|
– |
частота свободных колебаний; |
|
|
||
– |
начальная фаза колебаний. |
|
|
||
172

A [ y(0) / ]2 [ y(0)]2 , |
|
(7.8) |
arcsin[y(0) / A], arccos[ y(0) |
/ ( A)]. |
(7.9) |
|
|
|
Период свободных колебаний равен: |
|
|
T 2 / . |
|
(7.10) |
Отметим одно важное свойство свободных колебаний с одной степенью свободы: колебания всех точек системы происходят с одной и той же частотой, причем соотношение перемещений любых двух точек системы будет оставаться постоянной величиной в любой момент времени. Такие колебания мы будем называть собственными, а формы колебаний, описывающих конфигурацию системы, – собственными или главными формами колебаний. Следовательно, свободные колебания с одной степенью свободы всегда являются собственными колебаниями.
Если учитывать силы сопротивления движению, например
R v y, |
(7.11) |
|
то дифференциальное уравнение примет вид |
|
|
y 2ny 2 y 0, |
(7.12) |
|
где |
|
|
n / (2m 11). |
(7.13) |
|
При этом в случае n имеем затухающие колебания |
|
|
y Ae nt sin( t ) . |
(7.14) |
|
|
1 |
|
Здесь |
|
|
|
2 n2 |
(7.15) |
1 |
|
|
– частота затухающих колебаний. Период затухающих колебаний равен:
T* 2 / . |
(7.16) |
1 |
|
График затухающих колебаний показан на рис. 7.9.
Меру затухания можно определить как отношение двух последовательных амплитуд колебаний
y / y |
T* |
n |
|
|
|
=e 2 |
. |
(7.17) |
|||
|
|||||
i i 1 |
|
|
|
|
173
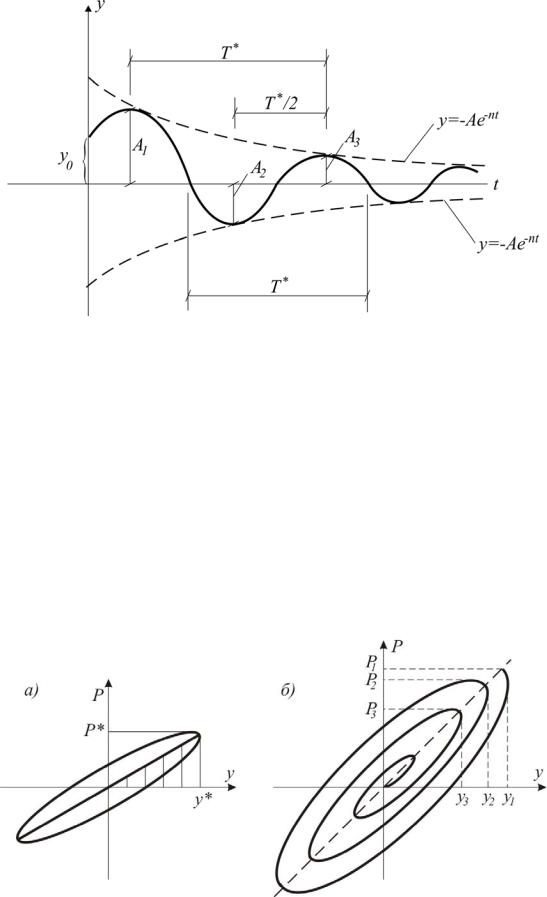
Рис. 7.9. График затухающих колебаний
|
T* |
n |
|
|
|
|
|
Величина e 2 |
называется декрементом колебаний, а показатель степени |
||||||
|
|||||||
nT* |
|
|
|
|
|
|
|
2 |
– логарифмическим декрементом колебания. Коэффициент п n |
|
|
– |
|||
|
|||||||
|
|
|
2m 11 |
|
|||
коэффициентзатухания.
Часто меру затухания рассматривают как рассеивание, или диссипацию, энергии движения, то есть необратимое преобразование ее в тепло. Диссипацию энергии движения за счет внутреннего трения можно показать с помощью графика зависимости «обобщенная сила P – обобщенное перемещение y » (рис. 7.10). При установившихся (вынужденных) колеба-
ниях этот график имеет вид эллипса (рис.7.10,а), или петли гистерезиса, для затухающихколебанийонимеетвидэллиптическойспирали(рис. 7.10,б).
Рис. 7.10. Петля гистерезиса
174

Мера затухания равна отношению величины рассеянной энергии W к величине работы упругих сил W , пропорциональной площади заштрихованного треугольника. Это отношение называется коэффициентом погло-
щения энергии
W / W. |
(7.18) |
Дифференциальное уравнение вынужденных колебаний имеет вид:
y 2ny 2 y 2 |
Р(t). |
(7.19) |
1p |
|
|
В случае, когда возмущающая нагрузка изменяется по гармоническому закону
P(t) Psin(t) , |
(7.20) |
где частота возмущающей силы, уравнение колебаний примет вид:
y A e nt sin( |
t ) A sin( t ) . |
(7.21) |
|||
|
1 |
|
1 |
2 |
|
Здесь |
|
|
|
|
|
A ( |
|
P) / |
(1 2 / 2 )2 4n2 2 / 4 ; |
(7.22) |
|
2 |
1p |
|
|
|
|
|
|
tg (2n / (2 2 ). |
(7.23) |
||
Так как с течением времени первое слагаемое уравнения (7.21) стремится к нулю, то приходим к установившимся вынужденным колебаниям
(рис. 7.11):
y A2 sin( t ). |
(7.24) |
Здесь сдвиг фазы вынужденых колебаний по отношению к фазе возмущающей силы.
Рис. 7.11
175
Так как 1p P y ст , то динамический коэффициент равен: для неконсервативных систем
y |
дин |
/ y |
A |
2 |
/ y |
cт |
1/ |
(1 2 / 2 )2 |
4n2 2 |
/ 4 |
(7.25) |
|
ст |
|
|
|
|
|
|
|
|||
для консервативных систем |
|
|
|
|
|
||||||
|
|
|
|
1 / (1 2 / 2 ) . |
|
|
(7.26) |
||||
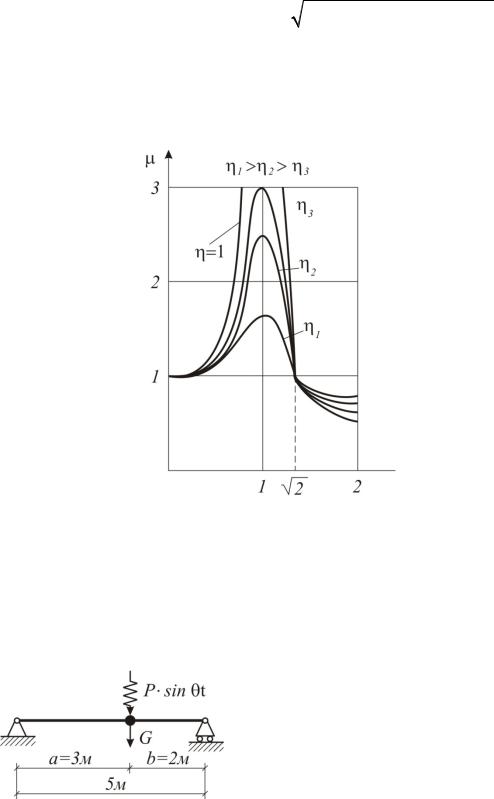
Очевидно, что при имеем явление резонанса (рис.7.12).
/
Рис. 7.12. Зависимость динамического коэффициента от соотношения частот
Примеры на колебания систем с одной степенью свободы
Пример №1. Используя динамический коэффициент для вибрацион-
ной силы P P0 sin t , |
действующей в электродвигателе общим |
весом |
|||
|
G 20000 H |
(рис.7.13), построить Mдин при |
|||
|
следующих |
данных: |
30 |
с 1, |
l 5 м, |
|
a 3 м, |
E 2,1 106 кг/см2 2,1 107 Н/м2 , |
|||
|
I 3773 см4 |
(двутавр |
№24), |
Р 1000 Н |
|
|
|
|
|
0 |
|
|
(амплитудное значение центробежной силы |
||||
Рис. 7.13 |
неуравновешенной части двигателя). |
|
|||
176
Решение:
|
1 |
|
|
, |
g |
. |
|
|
2 |
|
|
||||
|
|
|
|
y |
|||
|
1 |
|
|
|
|
СТ |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
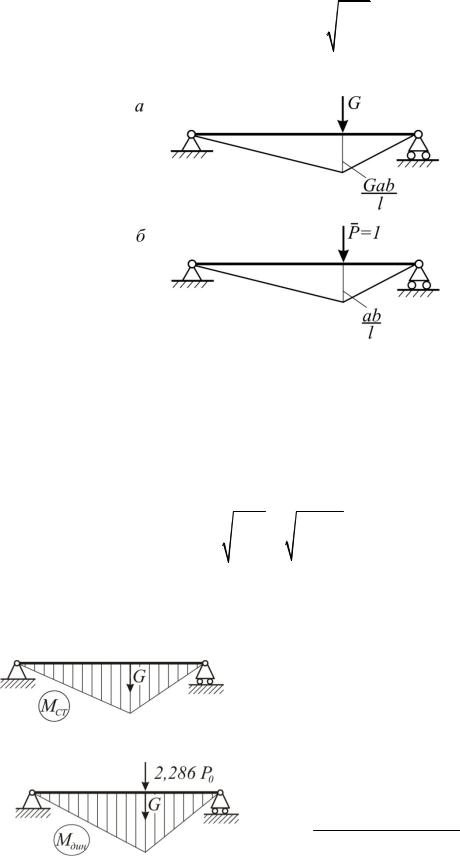
Определим статический прогиб от веса двигателя (рис.7.14).
|
|
|
|
|
|
|
|
|
|
|
Рис. 7.14 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
yСТ |
1 |
|
1 |
Gab |
a |
2 ab |
|
1 Gab |
b |
|
|
|
2 ab |
|
Ga2 b2 |
(a b) |
Ga2 b2 |
|
|||||||||||||||
|
|
2 |
l |
3 l |
2 l |
|
|
|
|
|
3 l |
|
|
|
3l |
2 |
EJ |
3l EJ |
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
20000 3002 2002 |
|
|
|
0,606 см. |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
3 500 |
2,1 107 |
3773 |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Частота свободных колебаний равна: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
981 |
|
40 c 1 . |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
y |
|
|
|
|
0,606 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
CT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Динамический коэффициент |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
2,286 . |
|
|
|
|
|||||||||||
|
|
|
|
|
|
1 |
2 |
|
1 |
|
302 |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
40 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
M |
G a b |
|
20000 3 2 |
24000 Н м |
|||||||||||||||||
|
|
Рис. 7.15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
5 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Мдин (2,286Р0 l G) a b 26743 Н м
Рис. 7.16
177

Пример №2. Определить приближенно динамическое напряжение в
балке (рис.7.17) от |
вертикальной |
составляющей центробежной силы |
||||
|
Р Р0 sin t |
двигателя, |
расположенного |
|||
|
посредине пролета |
балки. |
Вес двигателя |
|||
|
G 1500 кГ, вес неуравновешенной его части |
|||||
|
G1 300 кГ, эксцентриситет 1 |
см, частота |
||||
|
нагрузки |
30 с 1 , |
пролет |
балки l 4 м, |
||
|
балка |
двутавр |
№20, |
I 2500 см4 , |
||
Рис. 7.17 |
W 250 |
см3 , |
E 2,1 1011 Н/м2 , |
равномерно |
||
|
распределенная нагрузка q 4000 |
Н/м. |
||||
Прогиб от силы G, приложенной в середине пролета
(рис.7.18,а):
y1 Gl3 . 48EI
Прогиб от равномерно распределенной нагрузки:
|
|
y2 |
|
5ql4 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
384EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 7.18 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Полный прогиб |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
y |
y |
y |
|
Gl3 |
|
5ql4 |
|
|
|
|
15000 4003 |
|
5 4 4004 |
|
||||||||||||||
СТ |
1 |
|
2 |
|
|
48EI |
|
|
384EI |
|
|
|
|
48 2,1 106 2500 |
|
384 2,1 106 2500 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
0,38 0,254 0,634 см. |
|
|
|
|||||||||||||||
Частота свободных колебаний: |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
981 |
|
39,3 |
1. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
0,634 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|||||||||
Динамический коэффициент: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
2,396 . |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
302 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
(39,3) |
2 |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Центробежная сила от неуравновешенной части:
Р0 m 2 300981 302 1 275 кГ 2750 Н.
178

Эпюра изгибающих моментов от статической нагрузки:
МСТ(max) |
Gl |
|
ql |
2 |
15000 4 |
|
4000 42 |
23000 |
H м. |
4 |
8 |
|
4 |
8 |
|||||
|
|
|
|
|
|
Рис. 7.19
Напряжение в середине пролета от статической нагрузки:
МСТ 2300000 9200 H/см2 . W 250
Дополнительный изгибающий момент от динамической нагрузки:
Мдин |
Р0l |
2,396 |
2750 4 |
6589 H м. |
|
4 |
4 |
||||
|
|
|
Дополнительное динамическое напряжение при работе двигателя:
дин 658900 2636 Н/см2 . 250
Полное напряжение:
9200 2636 11836 Н/см2 .
Т.е. напряжения увеличились на:
92002636 100 29% .
Пример №3. Определить частоту свободных колебаний двухшарнирной рамы (рис. 7.20,а) с одной сосредоточенной массой в середине ригеля. Массой стоек по сравнению с массой ригеля пренебречь.
179

Решение.
Рис. 7.20
В связи с наличием горизонтальной связи в верхнем левом узле масса m может совершать только вертикальные колебания. Частота свободных колебаний рамы может быть найдена из соотношения
|
g |
|
1 |
|
. |
y |
m |
|
|||
|
|
aa |
|||
|
ст |
|
|
||
Для определения aa строим эпюру моментов от J 1. Т. к. рама статически неопределима, для решения используем метод сил:
X1 11 1p 0.
180
