
2545
.pdf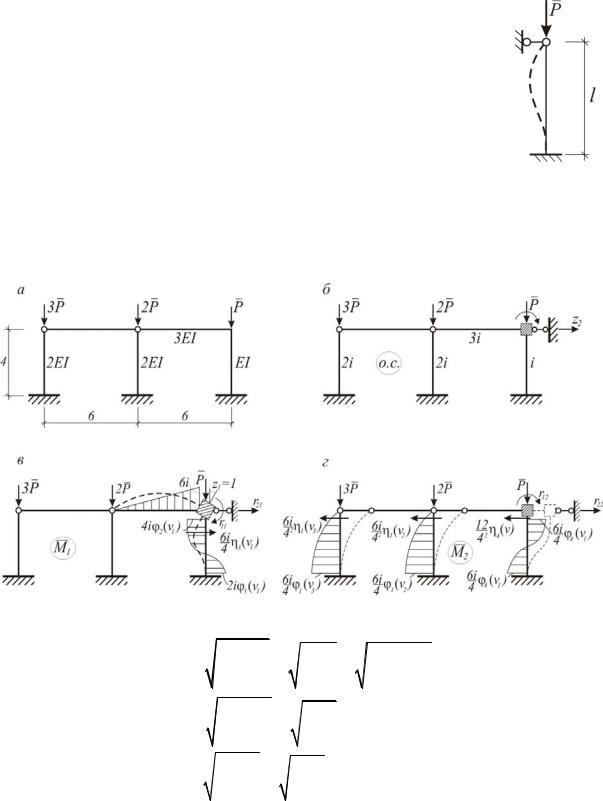
Это соответствует случаю, изображенному на рис. 6.22. При i1 0 получаем:
1(v) 0,
v / 2 1,57.
P |
|
2EI |
, |
|
кр |
|
4l2 |
|
|
|
|
|
|
|
что соответствует случаю консольного стержня. |
Рис. 6.22 |
|||
Пример № 5. Определить критическую нагрузку на раму (рис.6.23,а). Найдем соотношения между параметрами критической нагрузки
1, 2 , 3.
Рис. 6.23
v |
|
|
3P 42 |
|
|
24P |
|
|
1,5 |
16P |
1,225v; |
||||
|
|
|
|
|
|
|
|
|
|||||||
3 |
|
|
|
2EI |
|
|
|
EI |
|
|
|
|
EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
v |
|
|
2P 42 |
|
16P |
v; |
|
|
|||||||
2 |
|
|
|
2EI |
|
|
|
EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
v |
|
|
P 42 |
|
|
|
16P |
v. |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
1 |
|
|
|
EI |
|
|
|
EI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
r11 6i 4i 2 (v); |
|
|
|
|
|
|
|||||||||
r |
r |
6i |
|
|
(v) 1,5 |
|
(v). |
|
|
||||||
12 |
|
21 |
4 |
|
|
4 |
|
|
|
|
4 |
|
|
|
|
161
|
|
|
|
r |
|
|
6i |
|
1,225v |
|
6i |
(v) |
12i |
|
(v) |
|
|
|
||||||||||
|
|
|
|
16 |
|
16 |
16 |
|
|
|
|
|||||||||||||||||
|
|
|
|
22 |
|
|
1 |
|
|
|
1 |
|
|
2 |
|
|
|
|
||||||||||
|
|
|
|
|
3i |
1,225v |
(v) 2 (v) . |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
8 |
|
1 |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Уравнения метода перемещений: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
r11z1 r12 z2 |
0, |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r21z1 r22 z2 0. |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
D |
|
r11 |
|
r12 |
|
0. |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
22 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
r |
r r2 |
0. |
|
|
|
|
|
|
|
|
|
||||||
|
2i 3 2 (v) 3i |
|
|
|
|
|
11 |
22 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1,225v v |
2 v |
2,25i2 |
|
v 2 |
0. |
||||||||||||||||||||||
|
|
|
2 |
|
8 |
|
|
|
1 |
|
|
1 |
|
|
2 |
|
|
|
|
4 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
3 2 |
2 |
v 1,225v v 2 v 3 |
4 |
v 2 |
0. |
|
|
|
||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
Обозначим первую квадратную скобку А, вторую – В, третью – С. Тогда получим:
D A B C 0.
Решение трансцендентного уравнения методом подбора выполним в табличной форме (табл. 6.4).
Таблица 6 . 4
№ |
v |
1,225v |
2 (v) |
А |
1(1,225v) |
1(v) |
2 (v) |
В |
4 (v) |
С |
D |
п/п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2,3 |
2,818 |
0,81 |
4,62 |
-2,33 |
-1,186 |
0,468 |
-2,58 |
0,908 |
2,47 |
-14,39 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2,1 |
2,57 |
0,844 |
4,69 |
-1,7 |
-0,81 |
0,557 |
-1,4 |
0,926 |
2,57 |
-9,13 |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
1,8 |
2,205 |
0,887 |
4,77 |
-1,0 |
-0,32 |
0,675 |
0,03 |
0,945 |
2,68 |
-2,54 |
|
|
|
|
|
|
|
|
|
|
|
|
4 |
1,7 |
2,08 |
0,9 |
4,8 |
-0,8 |
-0,18 |
0,7 |
0,42 |
0,95 |
2,7 |
-0,68 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
1,65 |
2,02 |
0,906 |
4,812 |
-0,65 |
-0,105 |
0,727 |
0,699 |
0,954 |
2,73 |
+0,633 |
|
|
|
|
|
|
|
|
|
|
|
|
v 1,68;
Pкр v2EI 0,176EI (H). 16
На рис. 6.24 показана графическая интерпретация решения.
162
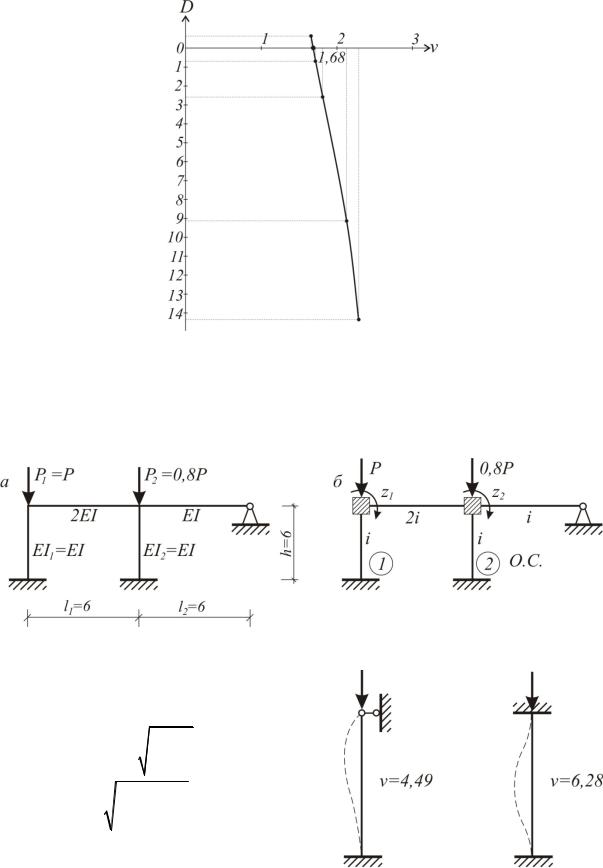
Рис. 6.24
Пример №6. Определить критическую нагрузку для рамы, изображенной на рис.6.25,а.
|
|
|
|
|
|
Рис. 6.25 |
Примем |
EI |
i, тогда 2EI |
2i . |
|||
|
6 |
|
|
|
6 |
|
|
v |
|
|
P 62 |
v, |
|
|
|
|
|
|||
|
1 |
|
|
EI |
|
|
|
|
|
|
|
|
|
v |
0,8 P 62 |
0,894v. |
||||
2 |
|
|
EI |
|
|
|
|
|
|
|
|
||
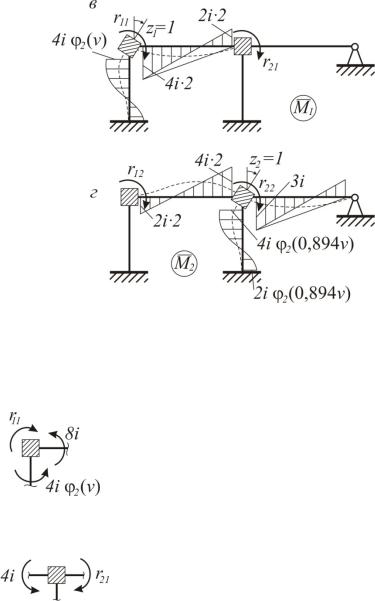
Пределы изменения v (рис. 6.26): |
||||||
|
4,49 v 6,28. |
Рис. 6.26 |
||||
|
|
|
|
|
|
163 |
Уравнения метода перемещений:
r11(v) Z1 r12 (v) Z2 0,
r21(v) Z1 r22 (v) Z2 0
Нетривиальное решение данной однородной системы уравнений:
D |
|
r11(v) |
r12 (v) |
|
0, |
|
|
||||
|
|
r (v) |
r (v) |
|
|
|
|
21 |
22 |
|
|
или
r11 r22 r122 0 .
Для решения детерминантного уравнения построим единичные эпюры и определим коэффициенты системы уравнений метода перемещений.
Рис. 6.27
Вырезая узлы, найдем riк .
r11 8i 4i 2 (v).
Рис. 6.28
r21 4i.
Рис. 6.29
164
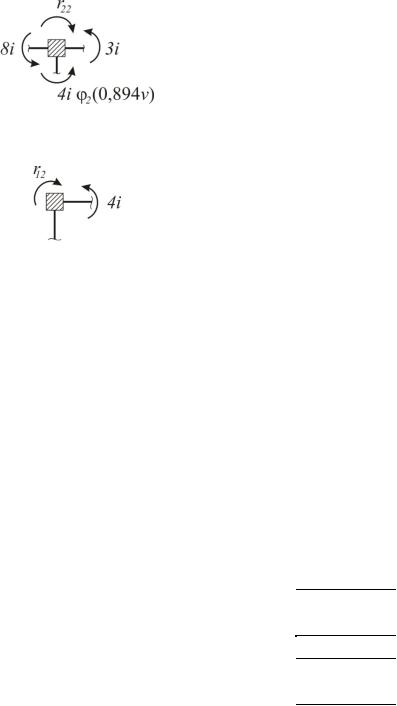
r22 11i 4i 2 (0,894v).
Рис. 6.30
r12 4i.
Рис. 6.31
Детерминантное уравнение примет вид:
4i 2 2 (v) 4i 2,75 2 (0,89v) 16i2 0.
Сокращая на 16i2 , придем к уравнению
2 2 (v) 2,75 2 (0,894v) 1 0 .
Обозначив первый сомножитель через А, а второй сомножитель через В, получим:
D A B 1 0 .
Составим таблицу расчета способом подбора корней трансцендентного уравнения.
|
|
|
|
|
2 (0,894v) |
Таблица 6 . 5 |
|
№ |
v |
0,894v |
2 (v) |
A |
B |
D |
|
п/п |
|
|
|
|
0,0307 |
|
|
1 |
5 |
4,47 |
-0,477 |
1,523 |
2,9 |
+3,37 |
|
2 |
5,75 |
5,14 |
-2,453 |
-0,453 |
0,67 |
2,071 |
-1,96 |
3 |
5,6 |
5,0 |
-1,748 |
0,252 |
-0,477 |
2,273 |
-0,427 |
Примем v 5,56.
Pкр v2EI 0,859EI (H) . 62
Графическое решение показано на рис. 6.32.
165
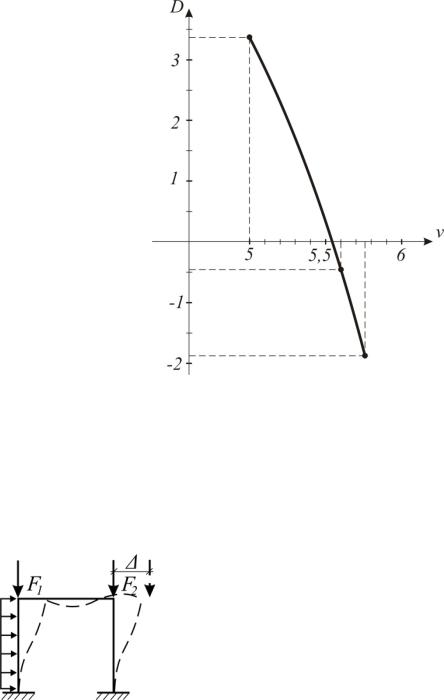
Рис. 6.32
6.10. Расчет рам по деформированной схеме
Элементы рам, стойки и ригели находятся под действием изгибающих и продольных сил, т.е. стержни находятся в условиях продольно-попе- речного изгиба. Обычный расчет рам на прочность производится по так называемой недеформированной схеме, т.е. усилия определяются для начального прямолинейно-осевого положения элементов и влияние продольных сил на изгиб не учитывается. Однако продольные силы вызывают дополнительные изгибающие моменты и перемещения (рис.6.33), а в ряде случаев изменяют и качественную картину усилий. Поэтому расчет с учетом влияния продольных сил оказывается более точным. Такой
Рис. 6.33 расчет называют расчетом по деформированной схеме или деформационным расчетом.
При деформационном расчете, так же, как и при обычном расчете на прочность, уравнения метода перемещений имеют вид:
r11Z1 r12Z2 .... |
r1nZn R1P 0; |
|
|||||||||
r Z |
r Z |
2 |
.... |
r |
Z |
n |
R |
0; |
|
|
|
21 1 |
22 |
|
|
2n |
|
2P |
|
|
(6.84) |
||
......................................................... |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
r Z |
r |
Z |
2 |
.... |
r Z |
n |
R |
0. |
|
|
|
n1 1 |
n2 |
|
|
nn |
|
nP |
|
|
|
||
|
|
|
|
166 |
|
|
|
|
|
|
|
Однако здесь все единичные коэффициенты и грузовые члены определяются с учетом действия продольных сил. Для вычисления единичных коэффициентов используется та же таблица метода перемещений, что и при расчете на устойчивость. Для вычисления грузовых членов строится дополнительная таблица метода перемещений. Эта таблица может быть получена путем решения дифференциального уравнения упругой оси:
|
EIyIV (Ny ) q(x). |
(6.85) |
Например, табличный случай защемленной балки с распределенной |
||
нагрузкой (рис. 6.34,а) принимает вид, показанный на рис. 6.34,б. |
|
|
а |
б |
|
Рис. 6.34
При этом, если при обычном изгибе (см. рис.6.34,а) M A M B |
ql2 |
, |
то |
||||
12 |
|||||||
|
ql2 |
|
|
|
|
||
при продольно-поперечном изгибе (см. рис.6.34,б) M A M B |
|
|
1 |
|
. |
||
12 |
4 ( ) |
||||||
|
|
|
|||||
Основная трудность деформационного расчета состоит в том, что окончательные продольные силы в стержнях рамы неизвестны. Поэтому в первом приближении их можно принять из произведенного заранее расчета по недеформированной схеме, а далее из результатов последовательно выполняемых расчетов по деформированной схеме.
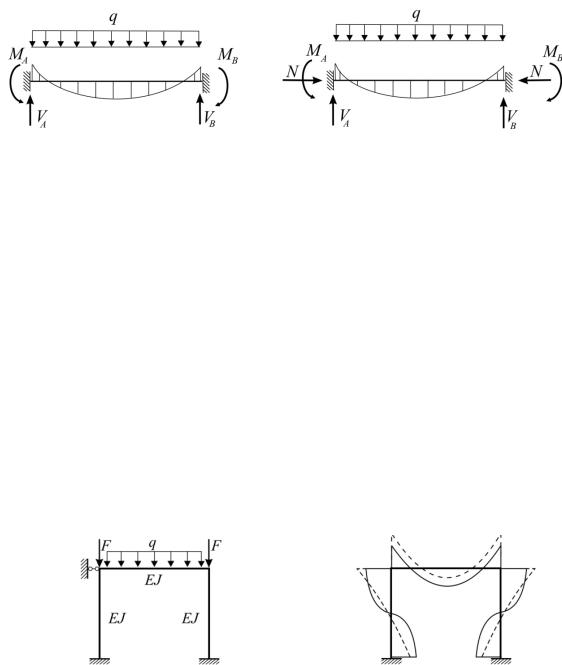
На рис. 6.35,б приведен расчет рамы (рис. 6.35,а) по деформированной схеме. Результаты расчета показаны сплошной линией. Для сравнения здесь же пунктиром обозначен расчет без учета продольных сил. Можно видеть, что учет продольных сил весьма существенно отражается на результатах расчета, изменяя не только величину, но и характер наибольших моментов.
а |
б |
Рис. 6.35
167
В опорных узлах изгибающий момент может увеличиться в несколько
раз.
На основе уравнений деформационного расчета легко построить систему уравнений для определения критической нагрузки, т.е. получить уравнения устойчивости.
Пусть вектор перемещений Z1 соответствует данному состоянию системы под нагрузкой, т.е.
RZ1 RP 0. |
(6.86) |
Если при данной нагрузке возможно второе близкое равновесное состояние, характеризуемое вектором Z1 Z , то система уравнений метода
перемещений для этого состояния имеет вид:
R(Z1 Z ) RP 0.
Вычитая из формулы (6.87) формулу (6.86), получаем:
RZ 0,
или
|
r11 |
r12 |
....r1n |
|
|
|
|||
|
r21 |
r22 |
....r2n |
0. |
|
.................... |
|
||
|
rn1 |
rn2 |
....rnn |
|
(6.87)
(6.88)
(6.89)
Последнее детерминантное уравнение позволяет определить критическую нагрузку на сооружение.
168
7. ДИНАМИКА СООРУЖЕНИЙ
7.1. Основные понятия
Динамика сооружений – это область строительной механики, в которой изучаются методы расчета и поведения сооружений при действии инерционных сил.
Любые нагрузки порождают ускорения, поэтому под статическими понимают такие нагрузки, когда ускорениями можно пренебречь, т.е их время приложения велико.
Если рассматриваются воздействия и процессы достаточно быстро протекающие во времени, то необходимо учитывать ускорения точек системы и возникающие при этом силы инерции.
Задачей динамики является определение напряженно-деформирован- ного состояния в любой точке сооружения во времени.
Кроме инерционных воздействий во многих случаях необходимо учитывать и силы сопротивления движения (диссипативные силы).
7.2. Динамические нагрузки
Внешние нагрузки могут весьма разнообразно изменяться во времени. Рассмотрим несколько видов динамического нагружения.
1. Гармоническая нагрузка Py |
Po sin t |
Рис. 7.1
2. Внезапно приложенная нагрузка
Рис. 7.2
169
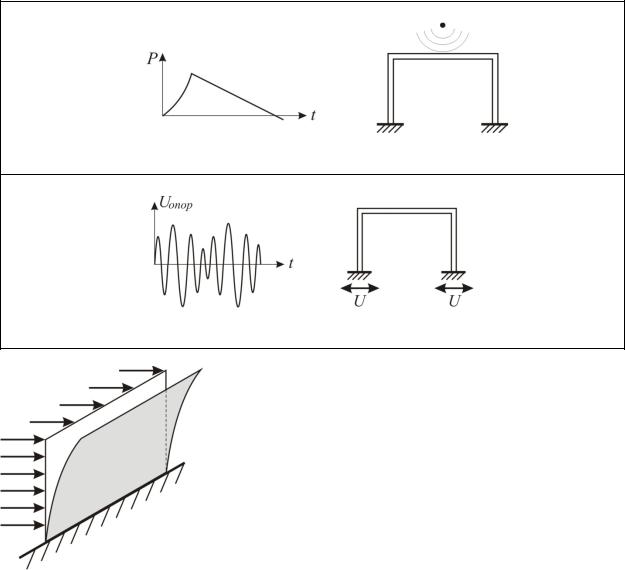
3. Ударная нагрузка (нагрузка от взрыва)
Рис. 7.3
4. Сейсмические воздействия
Рис. 7.4
Периодические нагрузки вида 1 и 4 вызывают вынужденные колебания зданий и сооружений. В некоторых случаях колебательное движение может вызвать и действие постоянных нагрузок. Например, автоколебания пластины происходят при обдувании ее потоком воздуха, имеющим постоянную скорость.
Основное внимание далее будет уделено
Рис. 7.5 |
исследованию колебаний сооружений. |
|
7.3. Число степеней свободы
Числом степеней свободы механической системы называют число параметров, полностью определяющих положение всех точек системы. В
динамике число степеней свободы напрямую зависит от количества сосредоточенных масс системы и от количества независимых перемещений этих масс.
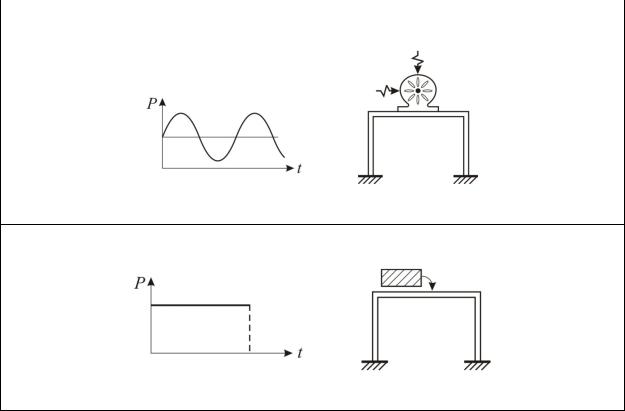
На рис. 7.6,а изображена система с одной степенью свободы, на рис.7.6,б – система с тремя степенями свободы, на рис. 7.6,в – система с двумя степенями свободы. На рис. 7.6,г учтено вращательное движение массы, и система имеет три степени свободы.
Системы с бесконечным числом степеней свободы (рис. 7.6,д) можно приводить к системам с конечным числом степеней свободы. Например,
170
