2545

Рис. 5.23

Mок М1 Z1 M p .

Пример №3. Пример расчета рамы с двумя неизвестными методом перемещений.

Определить усилия в раме, изображенной на рис.5.24,а. Р 24 кН; q 4 кН/м. На рис. 5.24,б показана основная система метода перемещений.

Уравнения метода перемещений имеют вид:

r11Z1 r12Z2 R1P 0;

r21Z1 r22Z2 R2P 0.

121

Рис.5.24

Рис. 5.25

122

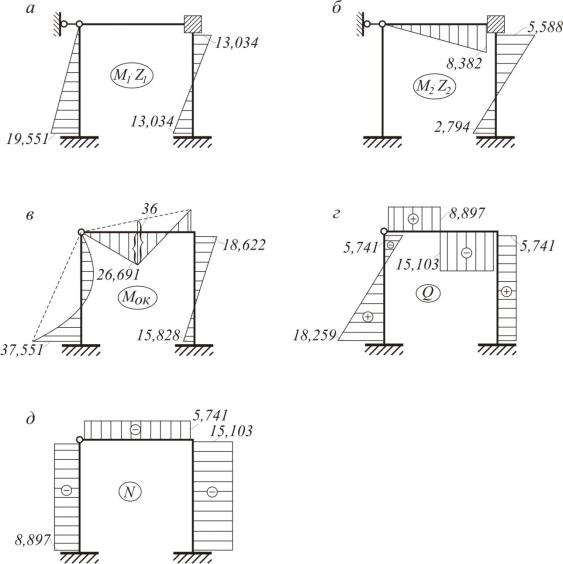
Строим исправленные эпюры (рис.5.29,а,б) и, складывая их с грузовой эпюрой, получаем окончательную эпюру моментов (рис.5.29,в). На рис.5.29,г,д показаны эпюры Q, N.

Рис. 5.29

Пример №4. Расчет рамы с наклонной стойкой (рис. 5.30,а).

Расчет рам с наклонными стойками имеет некоторые особенности. Здесь при определении единичных и грузовых реакций нужно учитывать продольные силы, возникающие в стойках. Кроме того, здесь при горизонтальных смещениях узлов происходят и вертикальные перемещения. Рассматриваемая рама дважды кинематически неопределима. Ее основная система показана на рис. 5.30,б. Система уравнений метода перемещений имеет вид:

r11Z1 r12Z2 R1P 0;

r21Z1 r22Z2 R2P 0.

124

Для определения коэффициентов и свободных членов уравнений строим эпюры (рис. 5.30,в; 5.32,б; 5.33,а).

Рис. 5.30

Для определения реакции r21 отделим ригель (рис.5.30,г) и составим уравнения равновесия:

Fky 0 :

0,75i 1,5i cos N1 sin 0,

N1 0,75i 1,5i 0,707 0,439i. sin

Fkx 0:

r21 64i sin N1 cos 0,

r21 1,5 0,707i 0,439 0,707i 1,605i 0,3103i 1,37i.

Реакцию r11 определяем из равновесия узла

(рис.5.31):

125

Рис. 5.33

Грузовые коэффициенты вычисляем по формуле Гвоздева:

Дальнейшее решение выполняется обычным образом.

5.6. Использование условий симметрии при расчете рам

методом перемещений

Данная рама (рис. 5.34,а) геометрически симметрична и трижды кинематически неопределима. Для расчета рамы используем группировку неизвестных:

Z1 z1 z2 , Z2 z1 z2; Z3 z3.

В результате исходная система уравнений метода перемещений

127

преобразуется к виду:

r22 z2 R2 p 0;

r11z1 r13z3 R1p 0;

r31z1 r33z3 R3 p 0.

Рис. 5.34

5.7. Смешанный метод расчета стержневых систем

Ранее рассмотрены два основных метода расчета стержневых систем – метод сил и метод перемещений. В методе сил за основные неизвестные принимались внутренние усилия Хi (лишние неизвестные), а в методе перемещений – это независимые перемещения узлов системы Zi. Лишние неизвестные находились из уравнений совместности деформаций, при этом каждое из уравнений приравнивало обобщенное перемещение, соответствующее внутреннему усилию xi, нулю. Перемещения Zi определялись из уравнений равновесия, в которых приравнивались нулю реакции в дополнительных связях.

128

В смешанном методе за основные неизвестные принимаются частично внутренние усилия Хi, а частично перемещения Zj. При этом уравнения смешанного метода будут двух типов: часть уравнений будет содержать условия совместности деформаций и выражать условие отсутствия перемещений в направлении лишних связей, а другая часть будет представлять условия равновесия.

Смешанный метод целесообразно применять для расчета таких рам, в которых одна часть имеет малое количество связей, а другая, наоборот, большое количество связей и малую подвижность.

Например, для рамы изображенной на рис.5.35,а, степень статической неопределимости равна:

W 3D 2Ш Соп 3 2 2 1 9 5.

Степень кинематической неопределимости n nу nл 3 2 5.

Для расчета левой части рамы, представляющей собой жесткий неподвижный контур, целесообразно применить метод перемещений. Для расчета правой части рамы лучше использовать метод сил, т.к. степень статической неопределимости этой части равна двум.

Таким образом, используем для расчета смешанный метод. Основная система этого метода показана на рис. 5.35,б.

Условием эквивалентности основной и заданной систем является равенство нулю взаимных перемещений сечений по направлению отброшенных связей и реактивного момента в наложенной на жесткий узел связи, т.е.

Развернув данные условия, получим систему канонических уравнений

r31,r32 – реакции от единичных сил.

129