2545

Рис. 5.5

Но в заданной системе дополнительной связи (заделки) нет. Следовательно, реакция в дополнительной связи от поворота узла и от нагрузки должна быть равно нулю:

или

Для построения единичных и грузовой эпюр метода перемещений необходимо знать значения узловых усилий от единичных перемещений и от нагрузки для отдельных балок. Для их расчета используют метод сил.

5.3. Канонические уравнения метода перемещений

Рассмотрим n раз кинематически неопределимую систему. Для расчета этой системы методом перемещений наложим на нее n связей. От единич-

ного перемещения j -й связи Z j 1 в i -й связи появляется реакция rij . От перемещения Z j – реакция rij Z j . От внешней нагрузки в i -й связи возникнет реакция RiP . Сумма реакций от всех узловых перемещений и от

должна быть равна нулю, т.к. в заданной системе этой связи нет.

Таким образом, условия равенства нулю реакций в дополнительных связях позволяют записать канонические уравнения метода перемещений:

вследствие чего матрица коэффициентов при неизвестных симметрична. Канонические уравнения метода перемещений, записанные в матрич-

ной форме, имеют вид:

Реакции rik и RiP определяют или из условий равновесия или путем перемножения эпюр.

112

5.4. Составление таблицы реакций метода перемещений

Произведем расчет отдельных статически неопределимых балок на кинематические и грузовые воздействия. Для расчета используем метод сил.

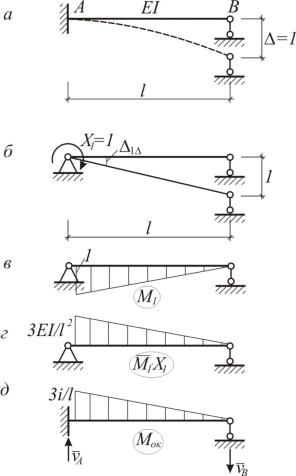
1. Определим концевые реакции в балке (рис. 5.8,а), вызванные взаимным смещением опор на 1.

Рис. 5.8

Данная система 1 раз статически неопределима. Основная система показана на рис.5.8,б. Единичная эпюра приведена на рис.5.8,в. Уравнение метода сил:

11X1 1 1 ;

113

Mок M1 X1. M A 3lEI2 3li .

VA VB Ml A l32i .

2. Определим концевые реакции для стержня, защемленного с двух сторон и загруженного равномерно распределенной нагрузкой (рис. 5.9,а).

Рис. 5.9

Данная система два раза статически неопределима. Основную систему выберем, используя группировку неизвестных (рис. 5.9,б). Единичные эпюры показаны на рис. 5.9,в,г. Эпюра M p изображена на рис. 5.9,д.

Система уравнений метода сил

11X1 12 X2 1p 0,21X1 22 X2 2 p 0.

114

распадается на два независимых уравнения:

11X1 1p 0,22 X2 2 p 0.

Т.к. 12 21 0. Но 1p также равняется нулю. Значит, x1 0.

Mок M2 X2 M p , ( рис. 5 . 9 е) .

Определим концевые реакции для стержня (рис.5.10,а), загруженного сосредоточенной силой в середине пролета.

Рис. 5.10

На рис. 5.10,б,в,г показаны основная система, единичная и грузовая эпюры. Уравнение метода сил

115

ставлена на рис. 5.10, д.

Аналогично строятся эпюры моментов и определяются концевые реакции для других случаев загружения или перемещения одного из узлов балки. Найденные решения приведены в таблице метода перемещений

(табл. 5.1).

Таблица 5 . 1

116

117

118

5.5. Примеры расчета рам методом перемещений

Пример №1. Построить эпюру усилий для рамы (рис.5.21,а).

Рис. 5.21

119

ic EJ6 i;

ic 2EJ4 EJ2 3EJ6 3i. r11 9i 4i 13i. R1p 40.

r11Z1 R1p 0.

Z1 R1p 40 . r11 13i

Строим исправленную эпюру М1Z1 (рис. 5.21,г) и складываем ее с грузовой.

Mок M P M1Z1.

Окончательная эпюра моментов показана на рис. 5.21,д. Далее строим эпюру Q (рис.5.21,е) и эпюру N (рис. 5.22,б).

Рис. 5.22

Статическая проверка (рис. 5.22,в):

Fky q 4 56013 48013 80 80 0.

Пример №2. Рама с линейным смещением узлов (рис. 5.23,а). Здесь неизвестно линейное смещение верхних узлов Z1. Основная

система показана на рис.5.23,б.

r11 363 i 3624 i 3627 i 34 i; R1p 165 P;

120