2545

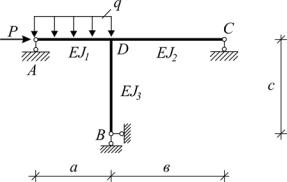
Примеры определения перемещений в статически неопределимых системах

Пример №1. Определить угол

EJ2 = 2EJ;

EJ3 = 3EJ.

Данная рама один раз статически неопределима. Определить угол поворота узла D можно тремя способами:

1. Построить две эпюры (от нагрузки и от единичного момента в узле D) в статически неопределимых системах.

2.Построить эпюру от нагрузки в статически неопределимой системе

Мнагрcт.неопр. . и эпюру от единичного момента ММcт.=1опр в статически опре-

делимой системе.

3.Построить эпюру от нагрузки в статически определимой системе

МРст.опр. и эпюру от единичного момента в статически неопределимой

системе Мст.опр.

М 1

Для построения эпюр воспользуемся методом сил. Найдем угол поворота первым способом. Уравнение метода сил.

11Х1 1Р 0.

101

Определение угла поворота узла D: 1-й способ

Результаты вычислений по всем трем способам совпадают.

4.11. Расчет конструкций на сочетание нагрузок. Построение объемлющих эпюр

Если кроме постоянной нагрузки имеются временные, которые могут действовать или не действовать в том или ином пролете, то необходимо находить такое сочетание постоянной и временных нагрузок, которое вызывает наибольшие и наименьшие изгибающие моменты, поперечные и продольные силы.

Для определения максимального момента Mmax в данном сечении к моменту от постоянной нагрузки Mпост прибавляют все положительные моменты от временных нагрузок Мвр в данном сечении.

Для определения минимального момента Mmin в данном сечении к моменту от постоянной нагрузки Mпост прибавляют все отрицательные моменты от временной нагрузки Мвр :

103

Эпюры, построенные по значениям Mmax и Mmin , называются объем-

лющими эпюрами. С помощью этих эпюр можно подбирать сечения балок с двухсторонней оценкой несущей способности.

Пример №1.

Дано: qпост 2 кН/м, qвр 3 кН/м, mвр 8 кН/м (см. рис.4.25,а).

Построить объемлющие эпюры моментов и поперечных сил для балки от постоянной нагрузки qпост и временных нагрузок qвр,mвр, Р1времен, Р2врем.

Построение объемлющих эпюр изгибающих моментов (рис.4.30,з) выполнено по формулам (4.35). Расчеты приведены в табл. 4.2. Эпюры от постоянной и временной нагрузок показаны на рис. 4.30,в,г,д,е,ж.

Таблица 4 . 2

Построение объемлющих эпюр поперечных сил выполняется по формулам:

Последовательность построения объемлющей эпюры поперечных сил показана на рис. 4.31.

104

Рис. 4.30

105

Рис. 4.31

106

5. МЕТОД ПЕРЕМЕЩЕНИЙ (РАСЧЕТ КИНЕМАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ)

Первые идеи метода перемещений встречаются в литературе как намеки, непонятные еще самим авторам. Так, Винклер в 1862 г. для расчета неразрезной балки вывел формулы, в которых изгибающие моменты в стержне выражены в функции от углов поворота его концов и от поворота стержня, но он не дошел до понимания того, что этот метод можно обобщить, и в дальнейшем изложении он постарался освободиться от этих переменных, выразив их через моменты. Бресс пошел несколько дальше и в 1865 г. вывел для неразрезной балки уравнение трех углов. Однако он тут же заметил: «Нам кажется излишним развивать дальше эти соображения, практические приложения которых будут очень ограниченными». Как видно, он отказался от развития идей, которые могли привести его к открытию метода перемещений, и не заметил их ценности.

Эти идеи постепенно развивались в форме решения отдельных задач в течение всей последней четверти XIX в. и первых десятилетий XX в. Так, еще в 1880-1890-х гг. были даны расчеты одного вида статически неопределимых систем – металлических ферм с жесткими узлами – с использованием углов поворота узлов в качестве основных неизвестных. В начале XX в. за рубежом появился ряд статей, посвященных расчету железобетонных рам с помощью тех же неизвестных. В 1920-х гг. метод деформаций уже оформился как самостоятельный метод, применимый ко всем статически неопределимым стержневым системам. В таком виде он изложен в книгах Бендиксена (1914) и Остенфельда (1926).

В России одной из первых работ по методу перемещений была вышедшая в 1901 г. книга проф. Е.О. Патона. В ней дан обзор всех опубликованных до того времени вариантов метода перемещений. В 1907 г. инженер Н.В. Некрасов опубликовал книгу, в которой рассмотрена схема точного решения задачи методом перемещений, свободная от ряда упрощающих допущений, принимавшихся его предшественниками.

После революции 1917 г. метод в России получил дальнейшее развитие. Были развиты понятия о простых и групповых реакциях, вызываемых упругими перемещениями, температурой и нагрузкой, и выведены формулы для них; представлены в канонической форме и в развернутом виде уравнения этого метода; разработаны способы упрощения уравнений и использования симметрии, а также комбинированный способ расчета рам. Проф. А.А. Гвоздевым предложен смешанный метод, представляющий собой синтез метода сил и метода перемещений. Составлены ценные таблицы, облегчающие расчет рам со стержнями ступенчатого и переменного сечений. Методу перемещений придана законченная форма классического метода.

107

В разработке метода перемещений принимали участие многие ученые: профессора А.А. Гвоздев, П.Л. Пастернак, Б.Н. Жемочкин, Н.И. Безухов, И.М. Рабинович, А.Б. Рабцевич и др. В отечественную учебную литературу и в проектную практику этот метод расчета рам вошел как один из самых простых и удобных.

5.1. Степень кинематической неопределимости

Методом сил рассчитываются статически неопределимые конструкции. За основные неизвестные в этом методе принимают внешние или внутренние силы, приложенные вместо отброшенных лишних связей. При этом взаимные перемещения сечений, где приложены эти силы, известны. Каждое уравнение метода сил выражает сумму перемещений по направлению данной отброшенной связи. В методе перемещений основными неизвестными будут перемещения (линейные или угловые) узлов стержневой системы. Для определения этих перемещений составляются уравнения равновесия. Число неизвестных перемещений узлов называют степенью кинематической неопределимости. Определив неизвестные узловые перемещения, находят внутренние силовые факторы (M, Q, N) в произвольных сечениях заданной системы.

Метод перемещений несет ряд допущений, таких, как:

а) неучитываетсявлияниепоперечныхипродольныхсилнаперемещения; б) для стержневых систем, состоящих из прямолинейных стержней, не

учитывается сближение узлов системы при деформации ее элементов. Узлы стержневой системы могут быть шарнирными или жесткими.

Шарнирный узел на плоскости имеет две степени свободы (рис. 5.1,а).

Рис. 5.1

Жесткий узел (рис.5.1,б) помимо линейных перемещений может получить еще и угловое перемещение в результате изгиба примыкающих к нему стержней, т.е. степень кинематической неопределимости равна:

108

Произведем подсчет степени кинематической неопределимости стержневой системы. Число неизвестных углов поворота всегда равно числу жестких узлов системы.

При определении числа независимых линейных перемещений узлов будем считать, что эти перемещения совпадают с возможными перемещениями системы, полученной из заданной путем введения во все жесткие узлы (включая и опорные) шарниров.

При этом число линейных смещений равно:

Для заданной рамы (рис.5.2,а), преобразованной к шарнирной (рис. 5.2,б), имеем:

nл 2 8 8 6 2 .

Количество линейных смещений можно определить и по формуле

W 3Д 2Ш Соп,

записанной для рамы, показанной на рис. 5.2,б.

Рис. 5.2

Заданная рама имеет три жестких узла, т.е. ny 3 .

Следовательно, степень кинематической неопределимости равна: n nл ny 2 3 5 .

Для рам с криволинейными стержнями необходимо учитывать возможное сближение концов криволинейных стержней после их деформации.

109

Например, для рамы, показанной на рис.5.3, число узловых смещений равно 4, т.к. надо учитывать изменение расстояния между узлами c и d из-за деформаций криволинейного стержня.

Рис. 5.3

5.2. Идея метода перемещений

Пусть требуется определить усилия в раме, изображенной на рис.5.4,а. В методе перемещений надо превратить раму в кинематически определимую. Для этого надо наложить количество дополнительных связей,

равное числу кинематической неопределимости. Для рамы (см. рис.5.4,а):

nл 0; ny 1;

n nл ny 1.

Рис. 5.4

Т.е. необходимо наложить 1 связь, препятствующую повороту жесткого узла. Неизвестное перемещение – угол поворота Z1.

Интересно, что данная рама трижды статически неопределима. Основные системы метода перемещений и метода сил показаны на рис. 5.4, б, в.

Дадим жесткой заделке единичный угол поворота Z1 (рис.5.5,а).

110