2545

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Пензенский государственный университет

архитектуры и строительства» (ПГУАС)

А.И. Шеин

КУРС СТРОИТЕЛЬНОЙ МЕХАНИКИ

Рекомендовано Учебно-методическим объединением вузов РФ по образованию в области строительства в качестве учебника

для студентов высших учебных заведений, обучающихся по программе бакалавриата по направлению 08.03.01 (270800) – «Строительство»

Пенза 2014

1

УДК 624.01/.07(075.8) ББК 38.112 Я 73

Ш39

Рецензент – доктор технических наук, профессор В.В. Смогунов

ПГУАС, 2014. – 312 с.

ISBN 978-5-9282-1107-3

Изложен краткий курс строительной механики для студентов, обучающихся по направлению «Строительство». Достаточно подробно рассмотрен кинематический анализ сооружений. Разобран расчет статически определимых рам и арок. Приведены основные энергетические теоремы. Изложен расчет статически неопределимых систем методом сил. Рассмотрен расчет кинематически неопределимых систем методом перемещений. Приведена теория и практика решения задач устойчивости и динамики зданий и сооружений. Рассмотрен расчет балок и рам на основе теории предельного равновесия. Изложена матричная форма решения задач механики. Приведены теоретические основы и примеры расчета конструкций методом конечных элементов.

Учебник подготовлен на кафедре механики и предназначен для студентов, обучающихся по программе бакалавриата по направлению 08.03.01 (270800) – «Строительство» строительных специальностей ВУЗов.

Учебник подготовлен в соответствии с утвержденной программой курса «Строительная механика» по ФГОС третьего поколения.

© Пензенский государственный университет

ISBN 978-5-9282-1107-3 архитектуры и строительства, 2014

Шеин А.И., 2014

2

ПРЕДИСЛОВИЕ

Предлагаемая книга является курсом строительной механики для бакалавров, а также может быть полезна магистрантам при изучении метода конечных элементов.

Содержание учебника соответствует разделам утвержденной УМО АСВ учебной программы, относящимся к стержневым системам. В нем отражен опыт преподавания данного курса на кафедре «Механика» ПГУАС. Содержание настоящего учебника заметно отличается от содержания существующих учебников по строительной механике. Автор стремился максимально доступно и компактно изложить строительную механику, используя при этом наиболее удачные разработки отдельных разделов, выполненные известными учеными и методистами. Особое внимание уделялось физическим основам методов и примерам их реализации. Подробные примеры расчета приводятся по каждому подразделу учебника. В отличие от большинства книг по строительной механике, изданных в последние годы, автор не стремился наполнить учебник матричным аппаратом. И только при изложении двух разделов курса – матричной формы решения задач механики и метода конечных элементов – был использован матричный аппарат линейной алгебры.

Основное место в учебнике занимает расчет стержневых систем. Такие системы находят достаточно широкое применение в несущих конструкциях различных сооружений. Кроме того, изложение основных теорем, понятий и методов строительной механики наиболее удобно и просто производить именно на основе стержневых систем. При практическом проектировании инженеру приходится сталкиваться с более сложными системами, в состав которых помимо стержней входят элементы и других типов: пластины, оболочки, массивные тела. При расчете таких двумерных

итрехмерных конструкций широко используется метод конечных элементов. Схема применения этого метода одинакова для всех конструкций. Поэтому, освоив методику применения метода конечных элементов для стержневых систем, инженер легко освоит расчет двух и трехмерных конструкций. В частности, такой подход показан в учебнике на примере решения плоской задачи теории упругости.

На примере стержневых систем обучающийся должен усвоить все основные понятия, свойственные численным методам расчета конструкций, в частности методу конечных элементов (метод перемещений, местная и локальная система координат, матрица жесткости элемента и всей конструкции).

Для систем из одномерных элементов можно произвести простые теоретические выкладки, разобрать и освоить такие разделы, как устойчивость

идинамика сооружений, предельное равновесие, «прощупать» практические задачи по этим темам.

3

КРАТКИЙ ИСТОРИЧЕСКИЙ ОЧЕРК

Множество направлений развития строительной механики несколько затрудняет хронологическое описание ее становления. Тем не менее имеется ряд книг, где рассматривается история развития науки о прочности материалов и конструкций. Здесь в первую очередь следует отметить книгу С.П. Тимошенко «История науки о сопротивлении материалов», в которой автор дал развернутую картину возникновения и становления науки о сопротивлении материалов и коснулся истории теории упругости и строительной механики стержневых систем. В книге упоминаются имена выдающихся ученых, работавших над созданием науки о прочности, приведены краткие биографические данные и основные результаты научных исследований.

Большой интерес представляют книга С.А. Бернштейна «Очерки по истории строительной механики», а также книга А.Т. Григоряна «Эволюция механики в России». Заслуживают внимания и такие популярные издания, как книги Дж. Гордона «Почему мы не проваливаемся сквозь пол» и «Конструкции и почему не ломаются вещи», книга М.И. Рейтмана «Залог прочности», учебное пособие А.И. Попова «История науки о сопротивлении материалов».

Механика – древняя наука, возраст которой насчитывает десятки веков. Уже в те отдаленные времена, когда людям пришлось заниматься строительством, они столкнулись с необходимостью располагать сведениями о прочности материалов и возводимых конструкций. Нет сомнения в том, что египтянам были известны некоторые эмпирические правила механики, поскольку без них нельзя было бы возводить грандиозные монументы, храмы, пирамиды, обелиски, некоторые из которых существуют поныне.

Греки внесли существенный вклад в дело развития строительного искусства: они разработали начала статики, лежащей в основе механики материалов. Архимед (287-212 до н.э.) доказал условия равновесия рычага и указал методы отыскания центров тяжести тел.

Широкий размах получило строительство у римлян. До нашего времени сохранились не только памятники и храмы, но и дороги, мосты, фортификационные сооружения. Римляне часто использовали арки, хотя они еще не знали, чем следует руководствоваться в выборе их надлежащего очертания и поэтому, как правило, придавали аркам форму полуокружности и ограничивались небольшими пролетами. Сравнение римских арок с современными арками показывает, что последние, являются более легкими. Следует отметить, что при проектировании других сооружений строители того времени пользовались исключительно полуинтуитивными и полуэмпирическими способами и опирались на опыт предшественников.

4

Опыт, накопленный в практике строительства греками и римлянами, был в значительной своей части утрачен на протяжении средних веков, и только в эпоху Возрождения это искусство было поднято на прежнюю высоту, оживился интерес к науке. Появились крупные мастера в области архитектуры и строительного искусства. Наиболее ярко дух эпохи воплотился в творчестве Леонардо да Винчи (1452-1519), который был не только великим художником, но и широко мыслящим ученым и инженером, сделавшим ряд крупных открытий в разных областях науки.

Леонардо да Винчи интересовала механика. По-видимому, именно он впервые применил идею принципа виртуальных перемещений, экспериментально изучил прочность строительных материалов, исследовал сопротивление балок изгибу и прочность колонн. Эти достижения да Винчи представляют собой, вероятно, первую попытку применения статики к определению сил, действующих на элементы строительных конструкций. Но эти ценные научные открытия остались лишь в записных книжках Леонардо, и инженеры ХV-ХVI вв. продолжали, как и в римскую эпоху, назначать размеры элементов своих сооружений, полагаясь лишь на практический опыт и догадку.

Первые попытки установить безопасные размеры элементов сооружений аналитическим путем относятся к XVII в., который стал эпохой быстрого развития математики, астрономии и естественных наук. К той эпохе относится творчество Галилео Галилея (1504-1542), выдающегося философа и математика, который увлекался метрономией, изучал вопросы гидравлики, баллистики, фортификации, судостроения. В последние годы жизни он начал изучать вопросы прочности балок, определил разрушающую силу в стержне и его предельное состояние при изгибе. В 1638 г. вышла в свет книга Галилея «Две новые науки», в которой он свел известные ему методы анализа в логическую схему. Эта книга знаменует собой возникновение науки о прочности, т.е. сопротивлении материалов или о механике деформируемого твердого тела.

Нельзя не отметить исследования Эдме Мариотта (1620-1684), который был разносторонним экспериментатором. Его опыты с воздухом привели к открытию закона, известного теперь как закон Бойля – Мариотта. В механике твердых тел Мариотт изучал соударения тел, растяжение и изгиб балок, прочность и упругие свойства материалов. Он пришел к выводу, что удлинение образцов всегда пропорционально силам. Таким образом, он почти одновременно с Гуком установил закон, известный теперь как закон Гука.

Одним из основоположников понятия об упругости материалов был англичанин Роберт Гук (1635-1702). Пропорциональность между нагрузкой и перемещениями он обнаружил еще в 1660 г. Гук изучал упругость конструкций, понимая, что свойства их упругости зависят от их размеров. В связи с этим появилось понятие жесткости сооружения.

5

ся вопросами устойчивости колонн и изгиба упругих полос. Хотя непосредственный вклад Лагранжа в строительную механику невелик и представляет больше теоретический, чем практический, интерес, его метод обобщенных координат ценен и нашел впоследствии применение при решении практических задач механики.

На протяжении XVIII и начала XIX вв. научные результаты предшествующих лет нашли практические приложения, и научные идеи, и методы былипостепенновведенывразличныеобластитехникииинженерногодела. К этому времени относятся учреждение первых высших технических учебных заведений и выход в свет первых печатных руководств по строительной механике. Францияопережалав этомнаправлении другиестраны, иизучениемеханики упругого тела продвигалось вперед главным образом благодаря активности французских ученых, таких, какЖ.А. Лагранж, Ш.О. Кулон(1736-1806),

Г. Монж (1746-1818), Л.М.А. Навье (1785-1836), Ж.В. Понселе (1788-1867), Д.Л. Коши (1780-1857), С.Д. Пуассон (1781-1840), Г. Ламе (1795-1870), Ю.П. Клапейрон (1799-1864), Б. де Сен-Ванан (1797-1886) и др.

В Англии и Германии к научным работам по строительной механике приступили лишь в XIX в. Здесь еще не было таких технических учебных заведений, которые могли бы сравниться с французскими по своему научному уровню. Тем не менее, хотя теоретическая научная работа по механике упругого тела и находилась в этих странах на относительно низком уровне, британскими и немецкими учеными и инженерами было решено много важных теоретических и практических проблем. Среди известных ученых Англии и Германии можно выделить Т. Юнга (1723-1820), Д.Ж. Максвелла (1831-1879), лорда Кельвина (1824-1907), лорда Релея

(1842-1919), Г. Лэмба (1849-1934), Л. Лява (1863-1940), Г.Р. Киргоффа (1824-1887), А. Клебша (1833-1872), О. Мора (1835-1911), Э. Винклера (1835-1888), Ф.Клейна (1849-1925) и др.

Значительный вклад в строительную механику внесли и многие выдающиеся российские инженеры и ученые: Д.И. Журавский (1821-1891), Ф.С. Ясинский (1856-1899), Н.А. Белелюбский (1845-1922), В.Л. Кирпичев

(1845-1913), В.Г. Шухов (1853-1939), Л.Д. Проскуряков (1858-1926) и др.

Труды перечисленных ученых заложили подлинно научные, прочные теоретические основы для окончательного формирования таких научных дисциплин, как сопротивление материалов, теория упругости и строительная механика стержневых систем. Во второй половине XIX в. были найдены общие методы раскрытия статической неопределимости, возникли теории пластин и оболочек, было намечено решение некоторых динамических задач и задач устойчивости. Техника получила достаточно надежные основы прогнозирования прочности проектируемых конструкций.

Типы инженерных сооружений в XX в. продолжали развиваться и усложняться, появились новые конструктивные формы и новые конструктивные материалы. Практика ставила перед теорией новые задачи. Наука о прочности стала развиваться теоретически и практически. Развитие ее

7

приняло лавинообразный характер, который сохраняется до наших дней. Об этом говорит, например, то, что количество публикаций по строительной механике составляет несколько тысяч книг, статей, рефератов, диссертаций, и каждый год это количество увеличивается на 10-15 тыс. исследований. При этом число исследований по расчету конструкций из неупругих материалов в последние годы растет в полтора раза быстрее по сравнению с исследованиями, относящимися к упругим конструкциям. Рекорд в последнее время принадлежит различным численным методам, в частности методу конечных элементов. Число посвященных этим методам публикаций удваивается каждые 3-4 года.

Используемый в строительной механике математический аппарат с каждым годом также существенно усложняется. В наши дни наряду с алгеброй, дифференциальными и интегральными уравнениями он включает теорию вероятностей, математическое программирование, матричное и векторное исчисления. Для того чтобы приобщиться к самым современным направлениям строительной механики, необходимо владеть математической теорией управления, тензорным и функциональным анализом, теорией групп и алгебраической топологии.

В связи с огромным числом публикаций по различным проблемам строительной механики в кратком обзоре невозможно привести имена всех выдающихся ученых, разрабатывавших эти проблемы в XX в., поэтому отметим имена только некоторых отечественных исследователей, заметив, что в XX в. строительная механика в России и СССР занимала передовые рубежи. В разработку методов расчета тонкостенных пространственных систем, в область математической теории упругости и пластичности значительный вклад внесли С.П. Тимошенко (1878-1972), А.Н. Крылов (1863-1945), Б.Г. Галеркин (1871-1946), Н.И. Мусхилишвили (1891-1976), Ю.Н. Работ-

нов (1914-1985), А.А. Ильюшин (1911-1960), В.З. Власов (1908-1958), П.Ф. Попкович (1887-1946), И.С. Бубнов (1872-1919), Н.И. Безухов (19031968), А.Р. Ржаницын (1911-1987), Б.Г.Коренев (1919-1998) и др. Большое количество сложных вопросов в задачах расчета статически неопределимых систем решено И.М.Рабиновичем (1886-1977), Н.С. Стрелецким

(1885-1967), А.А. Гвоздевым (1937-1996), П.Л. Пастернаком (1885-1963),

Б.Н. Жемочкиным (1887-1961) и другими учеными. Сложные проблемы расчета сооружений на устойчивость и действие динамических нагрузок рассматривались в трудах А.Н. Данника (1876-1950), К.С. Завриева (1891-1978), Н.В. Корноухова (1891-1953), А.Ф.Смирнова (1909-1986), В.И. Феодосьева

(1966-1991), А.П. Синицына (1889-1963), В.В. Болотина (1926-2008) и др.

Заметим, что здесь не приведены имена тех крупных ученых, которые трудились в конце XX в. и продолжают работать в настоящее время, обогащая строительнуюмеханикуновымиисследованиями.

8

1. ОСНОВНЫЕ ПОНЯТИЯ. СТАТИЧЕСКИ ОПРЕДЕЛИМЫЕ СИСТЕМЫ

1.1. Предмет и задачи строительной механики

Все создаваемые человеком инженерные сооружения (здания, мосты, плотины, корабли, самолеты и т.д.) требуют предварительного расчета, обеспечивающего надежность и долговечность их эксплуатации. Наука о методах расчета сооружений на прочность, жесткость и устойчивость называется строительной механикой. Задача строительной механики состоит в определении напряженно-деформированного состояния в любом интересующем нас сечении каждого из элементов реального сооружения. Широта вопросов, охватываемых строительной механикой, определяется спецификой расчетов на статические, динамические, тепловые воздействия, проверкой устойчивости равновесия. При этом та или иная задача может рассматриваться в линейной или нелинейной постановке, в детерминированном или вероятностном виде (т.е. при вполне определенных исходных параметрах или при наличии разбросов, относящихся к геометрическим размерам, физическим характеристикам и внешним воздействиям).

Строительная механика является постоянно развивающейся прикладной наукой, призванной обеспечить современными методами расчета строительство все усложняющихся инженерных сооружений. В связи с этим в ее развитии большое значение имеют опыт строительства и экспериментальные исследования, позволяющие оценить точность теоретических предпосылок и расчетов.

В настоящее время широкое распространение получили расчетные комплексы, базирующиеся на одном из методов строительной механики – методе конечных элементов. При этом все теснее становится связь строительной механики с проектированием конструкций и вычислительной математикой.

Для того чтобы изучить методы строительной механики и «почувствовать» работу сооружений под нагрузкой, рассмотрим стержневые системы. Изучение линейных стержневых систем является первой ступенью в освоении строительной механики.

1.2. Расчетная схема сооружения. Модели соединения элементов

Реальное сооружение, как правило, представляет собой совокупность отдельных элементов, работающих как единое целое в условиях внешних воздействий. Расчет реального сооружения с учетом всех особенностей его изготовления и эксплуатации является очень сложной задачей. Поэтому в

9

строительной механике моделью сооружения служит его расчетная схема, т.е. условная идеализированная схема, которая отражает наиболее важные свойства действительного поведения сооружения при тех или иных воздействиях и не учитывает второстепенные факторы, предполагаемые несущественными.

Таким образом, расчетная схема – это упрощенная схема сооружения, которая облегчает его расчет и возможно точнее отражает условия работы действительного сооружения.

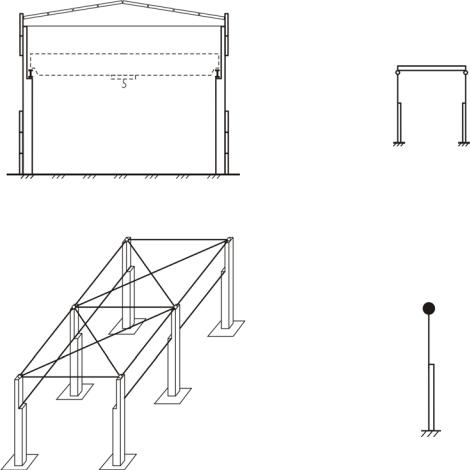
Одно и то же здание можно представить несколькими разными расчетными схемами, в зависимости от назначения расчета и рассматриваемых воздействий. Например, каркас одноэтажного промышленного здания (рис. 1.1), состоящий из ступенчатых колонн, двускатных балок покрытия, плит покрытия, стеновых панелей, остекления, подкрановых балок, мостового крана, может быть представлен в виде плоской рамы (рис. 1.2), пространственного каркаса (рис. 1.3) или невесомой стойки переменной жесткости с массой, сосредоточенной на конце (рис.1.4).

10