2516

В табл. 8.6 строка, соответствующая маркеру ОПТ, – приближение, принятое за оптимальное распределение электропроводности. НБ – реальное распределение электропроводности, наиболее близкое к оптимальному, которое можно получить из используемых в данной работе УВМ. Ээ – наилучшее распределение электропроводности, найденное экспериментальным путем; Эр – расчетное распределение электропроводности, соответствующее наилучшему экспериментальному.

Результаты расчетов и экспериментальных исследований показывают хорошее их согласование, а также эффективность использования предложенного метода расчета для оптимизации распределения металлического осадка по толщине проточного трехмерного электрода.

221

9. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭЛЕКТРОХИМИЧЕСКИХ ПРОЦЕССОВ С УЧЕТОМ ИЗМЕНЕНИЯ СКОРОСТИ ПРОТОКА ЭЛЕКТРОЛИТА В ОБЪЕМЕ ПТЭ В ТЕЧЕНИЕ ЭЛЕКТРОЛИЗА

Многочисленные теоретические и экспериментальные исследования электрохимических процессов, происходящих в объеме проточных трехмерных электродов (ПТЭ), как было указано выше, показали, что эффективность их работы во многом определяется удельной электропроводностью, величиной реакционной поверхности, плотностью тока и скоростью протока электролита. При этом многие характеристики и свойства электрохимических систем с ПТЭ существенно изменяются в процессе электроосаждения металлов на поверхности материала катода: меняются физические и электрохимические свойства границы раздела фаз, происходит зарастание и сужение пор ПТЭ и перераспределение скорости протока электролита по толщине проточного электрода.

Поэтому, с точки зрения поиска оптимальных условий электролиза на ПТЭ и управления процессом, важным является правильный выбор величины скорости протока электролита на входе в электрод и прочих управляющих процессом функционирования электрода параметров, в том числе и регулирующих распределение скорости протока в объеме проточного электрода.

Целью данного раздела являлось построение математической модели электрохимического процесса в проточном трехмерном электроде из углеродных волокнистых материалов с учетом изменения скорости протока электролита по толщине электрода, а также корректировка уравнения электрохимической кинетики, связывающего значении тока и потенциала при значительных изменениях скорости обтекания раствором углеграфитовых нитей. При этом учитывалось изменение удельной поверхности электрода, его электропроводности и пористости, а также коэффициента массопереноса за счет осаждения металла на нитях УВМ в процессе электролиза.

Пусть V (см3) – объем проточного электрода; ε – пористость углеграфитового материала; d (см) – диаметр волокон. Тогда суммарная длина волокон материала lg, суммарная площадь поверхности волокон Sg, диаметр волокна с осажденным металлом dm и суммарная площадь поверхности волокон с осажденным металлом Sm в объеме V электрода вычисляются по формулам:

222

SVm – удельную поверхность и εm – измененную пористость электрода будем рассчитывать по формулам:

SVm SVm и m mV ,

а изменяющуюся в процессе зарастания электрода металлом скорость протока раствора v (см/с) определим как отношение заданной объемной скорости протока mV (см3/с) к площади живого сечения электрода As A m ,

т.е. v mV .

As

Уравнение для плотности тока, используемое в математических моделях с целью учета совместного влияния электрохимических и гидродинамических условий на зависимость плотности тока от потенциала в проточных трехмерныхэлектродах [105], имеет вид:

где jпред zFC(x)km , а km – коэффициент массопереноса, вид которого для

ПТЭ из углеродных волокнистых материалов определен зависимостью

[167]:

km a ub .

Для ПТЭ коэффициент а отражает свойства электрода и раствора и зависит от пористости электрода, размера и конфигурации элементов пористого слоя, кинематической вязкости и коэффициента диффузии. Показатель b отражает гидродинамический режим и может колебаться в пределах от 0,3 для ламинарного до 0,8–1,0 для турбулентного потока. Обобщенные экспериментальные данные, приведенные в [43, 64], показывают разброс значений b в случае ламинарного потока 0,33–0,37, в случае турбулентного потока 0,49–0,71; коэффициент а изменяется в пределах 10–3–1,9·10–2. Таким образом, коэффициент массопереноса зависит от степени перемешивания (скорости протока электролита), от свойств углеграфитового материала (пористости, диаметра и конфигурации волокон УВМ).

В данном разделе монографии мы рассмотрим совместное влияние гидродинамических и электрохимических закономерностей процессов, имеющих

223

место в некотором элементарном объеме пористого трехмерного электрода, на вид поляризационной зависимости. При этом, в соответствие с представлениями о моделировании процессов в проточных трехмерных электродах [97, 105, 107], каждый элементарный объем ПТЭ отождествляется с некоторой точкой пространства в объемно-пористом электроде, в которой возможно протекание электрохимическойреакции.

Как и ранее [107], будем считать, что поток заряженных частиц i-го вида Wi (i 1,..., n) в объеме электролита определяется миграционной и кон-

вективной составляющими, что реализуется в большинстве электрохимических систем:

Здесь и далее zi , Ci (моль/см3), μi – соответственно заряд, концентрация и подвижность i-го электроактивного компонента в гомогенной или псевдогомогенной среде; F (Кл/моль) – число Фарадея; grad(U ) – градиент по-

тенциала электрического поля U (В); v – вектор скорости конвективного переноса электролита; div – дивергенция вектора.

Уравнение материального баланса можно записать в виде:

где κ (См/см) – величина, характеризующая электропроводящие свойства системы.

Уравнение (9.4) дополняется уравнением, связывающим концентрации и плотности тока всех компонент, участвующих в электродном процессе:

Аналогично [107], переходя от удельных электропроводностей к удельным сопротивлениям твердой – Т и жидкой – Ж фаз системы, по-

лучим уравнение:

224

Далее мы будем рассматривать квазиодномерные модели, которые наиболее часто реализуются в практике применения ПТЭ, что существенно упрощает алгоритмы расчетов. Заметим, что одномерная модель реализуется, когда в первом приближении можно считать идентичными процессы на любой прямой линии, параллельной координатной оси 0х, по толщине электрода при фиксированных значениях координат y и z.

При построении математической модели будем считать, что скорость конвективного переноса раствора распределяется в объеме ПТЭ и является функцией времени процесса, то есть v = v(t, х).

С учетом принятых представлений уравнения (9.2.5, 9.2.6) преобразуются к виду:

Полученную систему уравнений необходимо дополнить известными кинетическими уравнениями [26], связывающими значения плотностей тока и потенциала в точке x:

где J (А/см2) – габаритная плотность тока, проходящего через электрод; L – толщина электрода.

В случае, когда в электродной реакции участвует один компонент, а процесс можно считать квазистационарным, система (9.8) – (9.11) преобразуется к виду:

225

U(x,0) R .

Вработах [98, 101, 108] показано, как учитывать в математической модели изменение электропроводности твердой и жидкой фаз электродной системы от координаты по толщине электрода, которая может существенно меняться в процессе электролиза.

Вуравнениях (9.7), (9.9), (9.12), (9.15) участвует функция v(x, t) – ско-

рость протока электролита, и её частная производная vx (х,t) . Для вычис-

ления этих функций введем в рассмотрение следующие параметры: mV – постоянную объемную скорость протока электролита через электрод; ε0 – величину, характеризующую пористость электрода в начале электрохимического процесса и ε(х,t) – пористость электрода в точке ПТЭ с координатой х в момент электролиза t.

Нетрудно получить следующие соотношения:

точке х в момент времени t.

Элементарные преобразования этих соотношений приводят к следую-

Величины M(x,t) и Mx (x,t) рассчитаем следующим образом. ПустьM (x,t t) M (x,t) x – привес металла за время t для слоя ПТЭ с

226

единичным сечением и толщиной x ; c c(x,t) c(x x,t) – изменение

концентрации электроактивных ионов в элементарном объеме электролита при прохождении его от точки x до точки x x ; c mV – изменение

концентрации ионов в элементарном объеме при прохождении от точки x до точки x x в единицу времени; c mV t – то же за время t или,

что то же самое, количество металла, осевшего в элементарном объеме в ПТЭ с единичным сечением и толщиной x (в точке x ). Для перечисленных выражений можно записать соотношения:

Коэффициент массопереноса Km также необходимо считать переменной величиной, зависимой как от координаты точки в ПТЭ, так и от текущего времени процесса:

Скорость протока электролита может существенно изменяться в различных точках ПТЭ: либо возрастать при зарастании электрода металлическим осадком, либо убывать при стравливании осадка, что, согласно уравнению (9.22), влияет на величину коэффициента массопереноса.

По представленным выше математическим моделям были разработаны программы для ПЭВМ и проведены численные расчеты процессов в ПТЭ с катодами из углеграфитовых волокнистых материалов марок АНМ, ВИНН-250 и ВНГ-50 при различных исходных скоростях потока электролита, подаваемого на ПТЭ, для различного времени ведения процесса электролиза. Свойства углеродных волокнистых материалов, использованных в работе, приведены в табл. 9.1.

Экспериментальные исследования влияния гидродинамических режимов электролиза на распределение и показатели процесса электролиза в проточном трехмерном электроде проводились на примере электроосаждения меди из кислого сернокисло-аммониевого электролита. Схема установки для проведения экспериментов изображена на рис. 9.1.

Подвергаемый электролизу раствор, содержащий (г/л): Cu – 0,16, H2SO4 – 25, (NH4)2SO4 – 80, циркулировал между емкостью с раствором и электролитической ячейкой. Удельная электрическая проводимость раствора 0,101 См/см. Концентрацию ионов меди в растворе в заданном узком интервале 0,16 ±0,03 г/л в процессе электролиза обеспечивали добавлени-

227

ем определенного объёма основного электролита меднения (г/л): CuSO4 ·

5H2O – 170, H2SO4 – 25, (NH4)2SO4 – 80.

Таблица 9 . 1 Свойства углеродных волокнистых материалов [43, 47, 64]

Рис. 9.1. Схема экспериментальной установки:

1 – электролитическая ячейка; 2 – ёмкость с раствором; 3 – источник постоянного тока; 4 – насос; 5 – амперметр

Динамику электроосаждения меди на УВЭ изучали в зависимости от габаритной плотности тока (500–2500 А/м2), скорости протока раствора (0,1–1,0 мл/с·см2) на углеродные волокнистые электроды с различной исходной электропроводностью. Электроосаждение меди проводили на электроды, состоящие из пяти слоёв указанных ранее УВМ, общей толщиной 6 мм, при этом отношение габаритной поверхности катода к объему раствора в емкости с электролитом составляло 0,2 м2 : 500 л, что соответствует реальному технологическому процессу. Исследования проводили в

228

гальваностатических условиях при тыльной подаче раствора в электрод с тыльным токоподводом (сторона электрода, прилегающая к токоподводу, тыльная – Т).

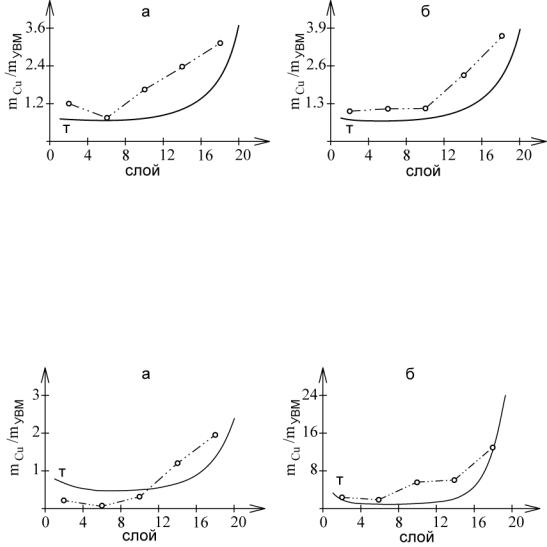
На рис. 9.2, 9.3 представлены некоторые результаты расчетов и экспериментальных исследований распределения осадка металла по толщине ПТЭ. В расчетах общая толщина электрода разбивалась на 20 расчетных слоев. При этом на оси ординат показано отношение массы электроосажденной меди к массе УВМ (mCu/mУВМ).

Рис. 9.2. Расчетное (сплошная линия) и экспериментальное (точки) распределение медного осадка по толщине электрода из УВМ ВНГ-50; исходная скорость протока раствора v, см/с: а – 0,4; б – 1,0; габаритная плотность тока J, А/м2: а и б – 500, время электролиза t, мин: а и б –180

Удельная электропроводность углеграфитового материала типа ВНГ-50 составляет 0,46 См/см, что больше электропроводности электролита (рис. 9.2).

Рис. 9.3. Расчетное (сплошная линия) и экспериментальное (точки) распределение медного осадка по толщине электрода из УВМ ВИНН-250; габаритная плотность тока i, А/м2: а –500; б – 2500; начальная скорость протока раствора v, см/с: а и б – 1,0; время электролиза t, мин: а и б –180

Удельная электропроводность углеграфитового материала типа ВИНН-250 составляет 0,10 См/см, что соизмеримо с электропроводностью электролита (рис. 9.3).

229

Приведенные результаты свидетельствуют о сопоставимости результатов расчетов и экспериментальных данных. Это позволяет изучать электрохимические процессы, происходящие в проточных трехмерных электродах, методом математического моделирования с учетом изменения скорости протока раствора по толщине электрода в процессе осаждения металла и основных характеристик электрохимической системы (удельной поверхности, электропроводности, пористости электрода, коэффициента массопереноса).

В табл. 9.2. представлены результаты расчетов равномерности распределения и веса металла на ПТЭ с катодами из углеграфитовых волокнистых материалов марок ВИНН-250, ВНГ-50 и АНМ при различных плотностях тока и различных скоростях протока электролита.

Таблица 9 . 2

Показатели распределения металла по толщине электрода: max/min – отношение максимального к минимальному количеству металла, определенного расчетным путем, при делении электрода единичного сечения на 5 равных частей; max – отношение массы металла к массе УВМ на части электрода с максимальным осадком; min – отношение массы металла к массе УВМ на части электрода с минимальным осадком; время электролиза 180 мин

230