2488

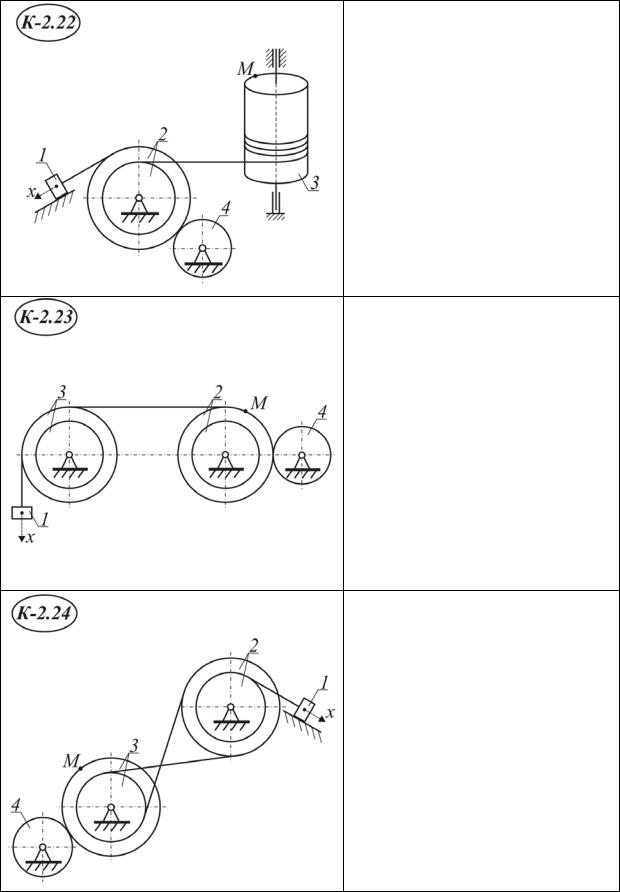
Продолжение табл. I I . 2 . 1

Радиусы:

R2=50 см r2=20 см R3=60 см R4=10 см

При t=0 x0=8 см, v0 =4 см/с При t=t2: x2=119 см

Расчётные моменты времени:

t2=3с, t1=2с.

Закон движения груза 1:

х аt2 v0t x0

2

Радиусы:

R2=32 см r2=16 см R3=32 см r3=16см R4=10 см

При t=0 x0=6 см, v0 =14 см/с

При t=t2 x2=862 см

Расчётные моменты времени:

t2=4 с, t1=2 с.

Закон движения груза 1:

х аt2

2

Радиусы:

R2=40 см r2=18 см R3=40 см r3=18см R4=10 см

При t=0 x0=5 см, v0 =10 см/с

При t=t2 x2=193 см

Расчётные моменты времени:

t2=2 с, t1=1 с.

Закон движения груза 1:

х аt2 v0t x0

2

71

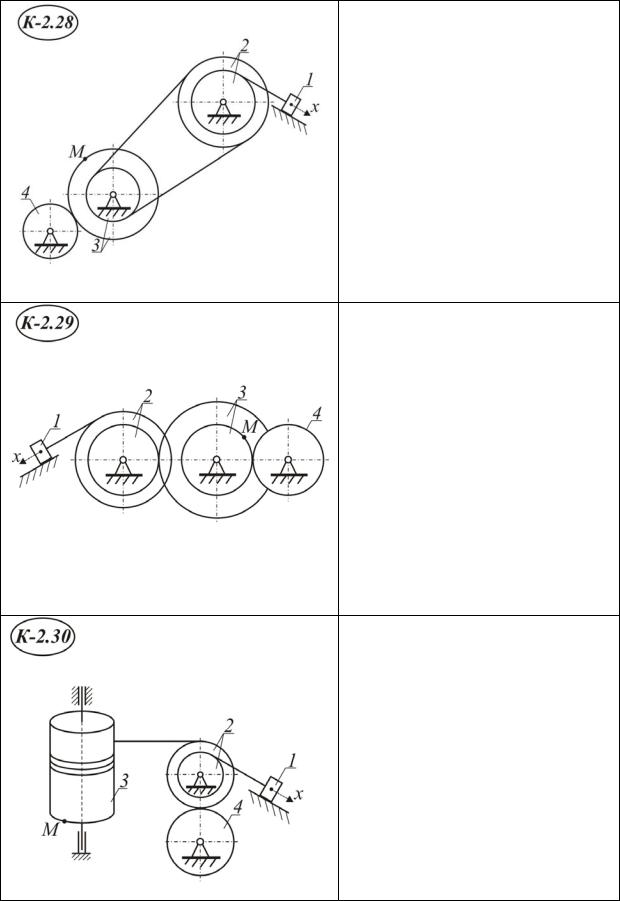
Окончание табл. I I . 2 . 1

Радиусы:

R2=40 см r2=20 см R3=40 см r3=15см R4=20 см

При t=0 x0=8 см, v0 =5 см/с При t=t2 x2=347 см

Расчётные моменты времени:

t2=3 с, t1=2 с.

Закон движения груза 1:

х аt2 v0t x0

2

Радиусы:

R2=25 см r2=20 см R3=50 см r3=25см R4=20 см

При t=0 x0=4 см, v0 =6 см/с При t=t2 x2=32 см

Расчётные моменты времени:

t2=2 с, t1=1 с.

Закон движения груза 1:

х аt2 v0t x0

2

Радиусы:

R2=30 см r2=15 см R3=20 см

R4 25 см.

При t=0 x0=10 см, v0 =7 см/с

При t=t2 x2=128 см

Расчётные моменты времени:

t2=2 с, t1=1 с.

Закон движения груза 1:

х аt2 v0t x0

2

72

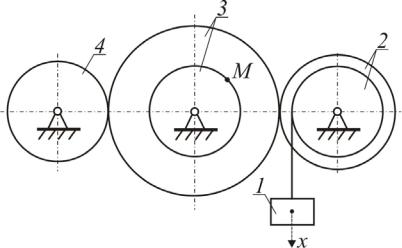
Пример выполнения задания К-2

t2 5 c .

Закон движения груза

x at2 V0t x0. 2

Определить в момент времени t1 2 c скорость и ускорение груза,

скорость и ускорение точки М одного из колес механизма, угловые скорости и ускорения всех колес механизма.

Рис. II.2.1 Заданная схема механизма

Решение:

1. По закону движения груза найдем ускорение груза а. При t2 5 c

Скорость груза

v dxdt x.

Так как

x at2 v0t x0 11.92t2 4t 2, 2

то v 23,84t 4.

73

2. Определяем угловые скорости и ускорения всех колес.

2 v 23,84t 4 2,98t 0,5 . r2 8

При t1 2 c

ω2 6,46 рад/с .

Для определения угловой скорости третьего колеса запишем уравнение, связывающее искомую величину с известной угловой скоростью второго колеса:

R2ω2 R3ω3,

следовательно,

ω3 R2ω2 16(2,98t 0,5) 3,4t 0,57. R3 14

При t1 2 c

ω3 7,37 рад / с.

Угловую скорость четвертого колеса найдём, зная, что при зацеплении колёс угловые скорости обратно пропорциональны радиусам R:

ω4 R3 14 1,75, ω4 1,75(3,4t 0,57) 5,95t 1.

ω3 R4 8

При t1 2 c

ω4 12,9 рад/с.

Так как значение углового ускорения тела в данный момент времени равно первой производной от угловой скорости, то

ε2 ω2 2,98 рад/ с2;

ε3 ω3 3,4 рад/с2;

ε4 ω4 5,95 рад/с2 .

3.Скорость и ускорение точки М при t1 2 c

vM r3ω3 10 7,37 73,7см/с;

74

aMτ r3 ε3 10 3,4 34 см/с2 ;

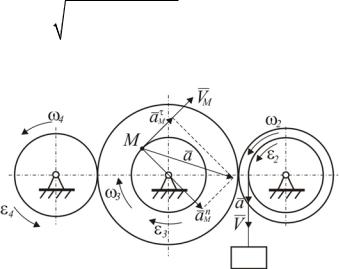
Покажем найденные величины на рис. II.2.2

Рис. II.2.2. Кинематические характеристики шкивов и точки М в момент времени t1

3. Плоское движение твёрдого тела

Задание К 3. Определение скоростей и ускорений точек многозвенного механизма

Плоский механизм состоит из стержней 1, 2, 3, 4 и ползуна В или Е, соединённых друг с другом и с неподвижными опорами О1, О2 шарнирами.

Определить для заданного положения механизма скорости точек А, В, Д, Е, угловые скорости всех звеньев, ускорения точек А и В, угловое ускорение звена АВ.

Схемы механизмов и необходимые для расчёта данные показаны в табл. II.3.1.

Указания. Определить скорости точек механизма можно с помощью мгновенного центра скоростей или по теореме о проекциях скоростей двух точек тела.

Для определения ускорений точек механизма следует воспользоваться теоремой об ускорениях точек плоской фигуры: аВ аА аВА аВАn . При непрямолинейном движении ускорения точки ( aА или aB ) надо представлять в виде двух составляющих – тангенциальной и нормальной

75

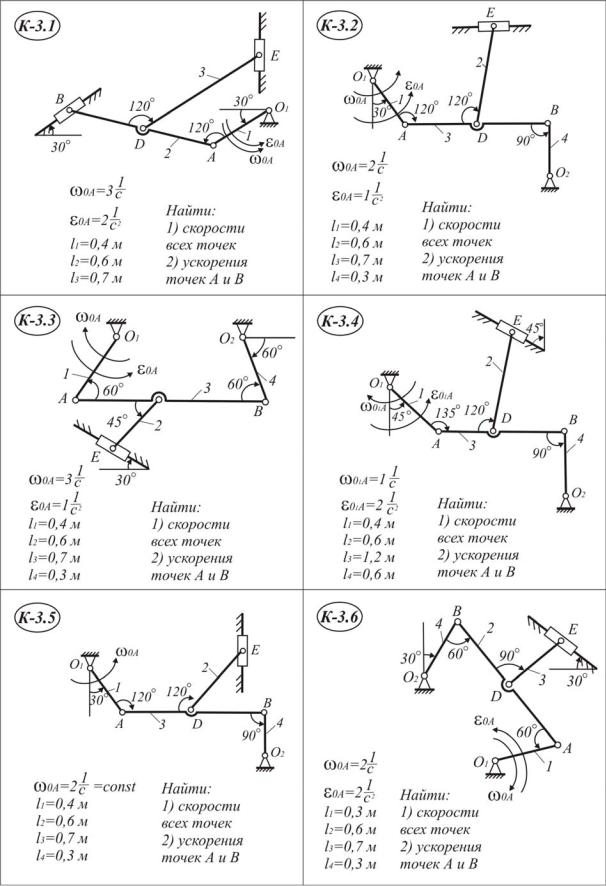
Таблица I I . 3 . 1

76

П р о дол жение табл. I I . 3 . 1

77

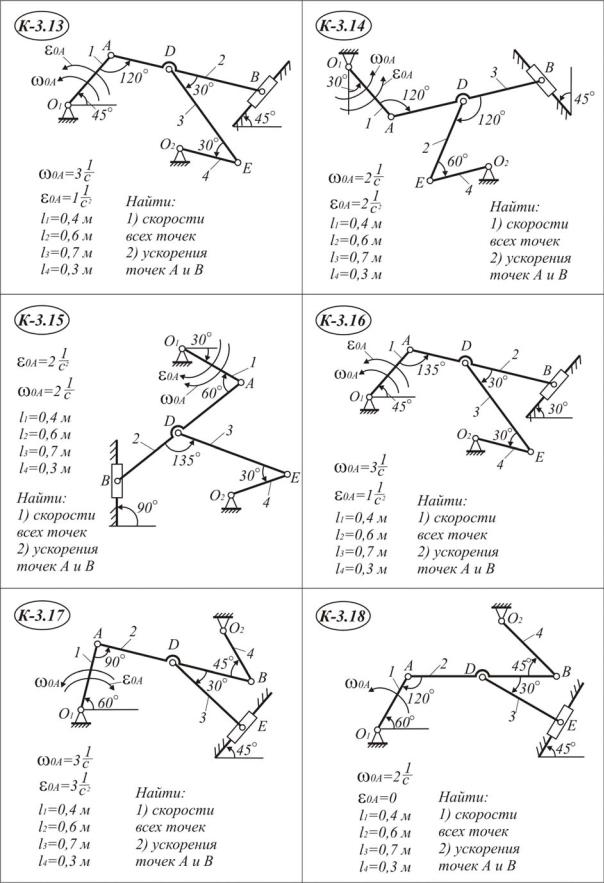
П р о дол жение табл. I I . 3 . 1

78

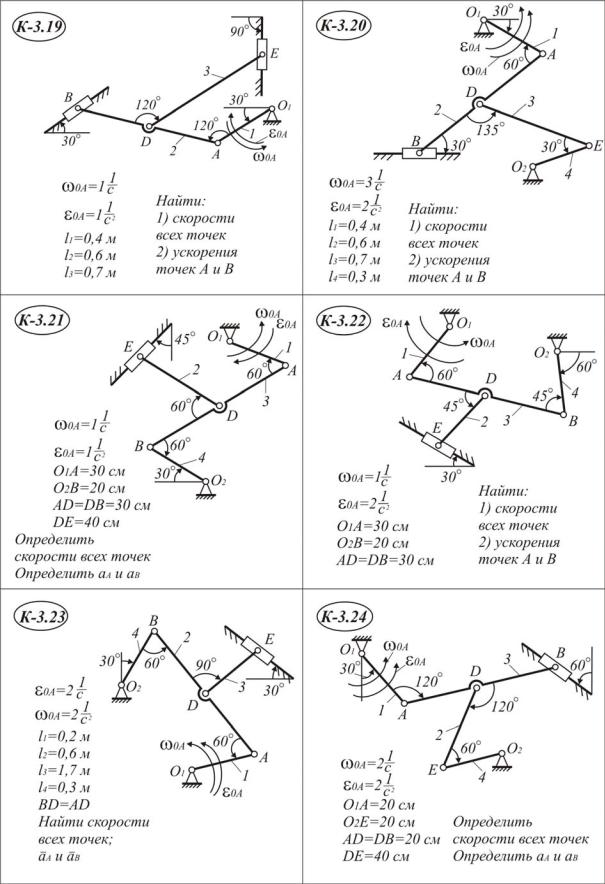
П р о дол жение табл. I I . 3 . 1

79

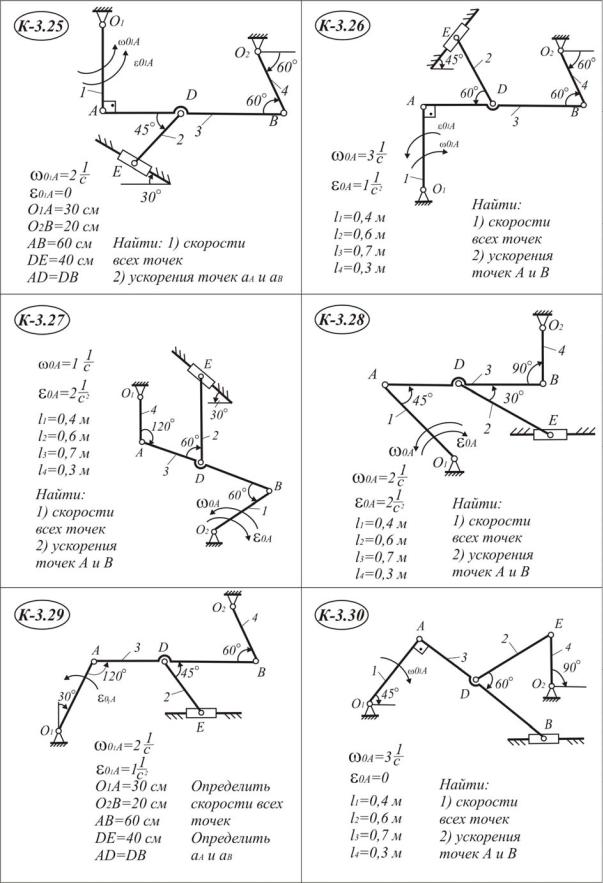
Окончание табл. I I . 3 . 1

80