
2488
.pdf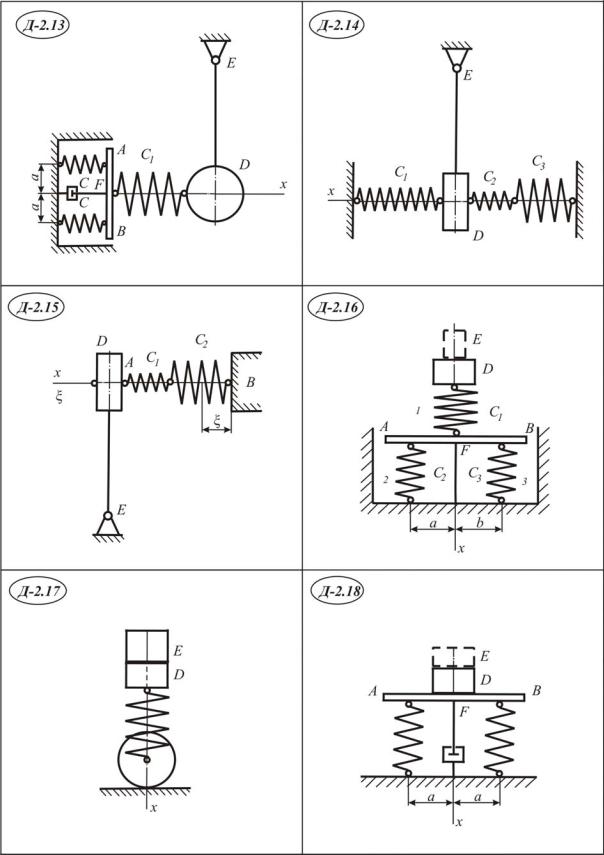
111
112
113
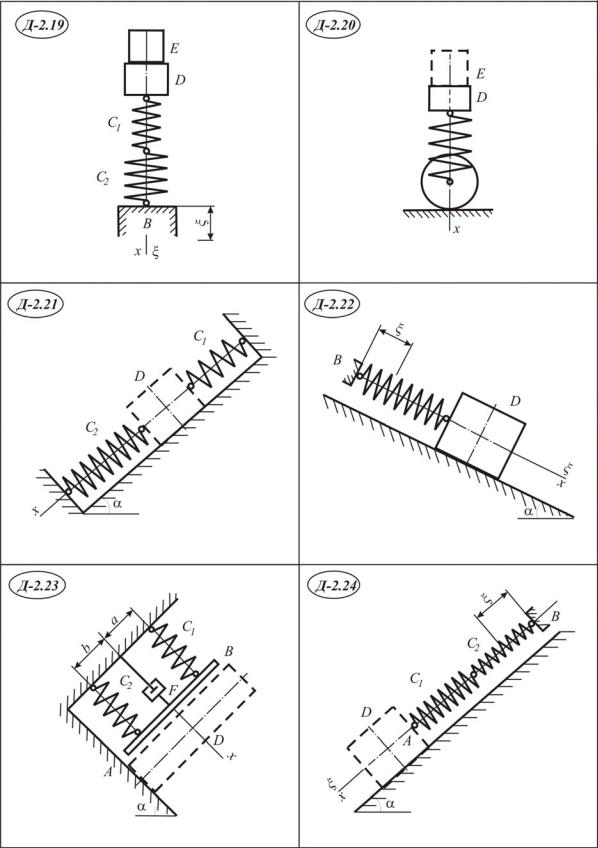
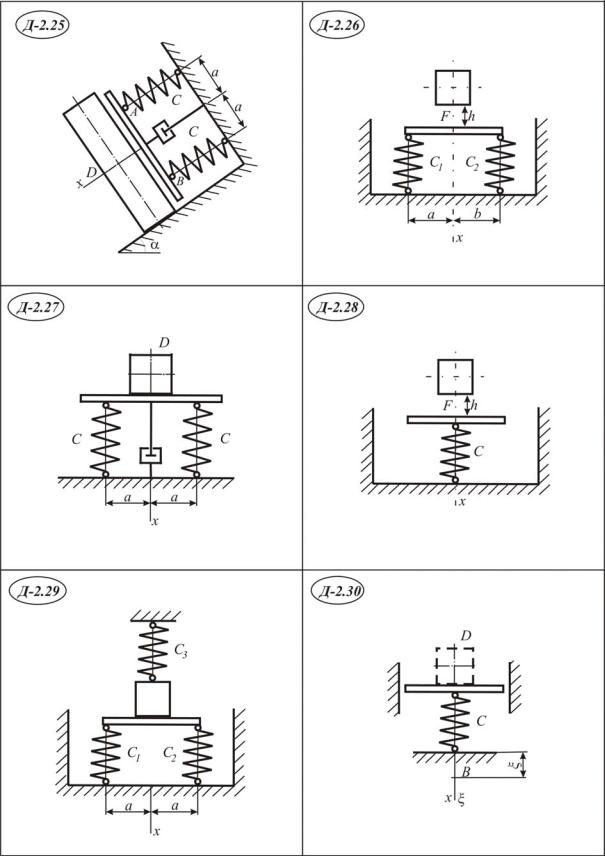
Пример выполнения задания Д-2
На горизонтальном столе лежат две последовательно соединённые пружины с жесткостями C1 = 4 Н/см и C2 = 12 Н/см (рис. III.2.1). Они
колеблются по закону d sin pt , |
где d 4 см, |
p 8 c 1 . К ним при- |
креплен груз с массой m = 1 кг. Колебание происходит в сторону положительного направления оси х. Начальная скорость v0 0 .
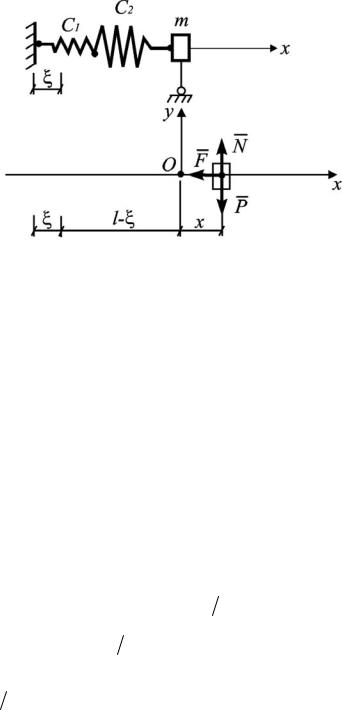
Рис. III.2.1
Решение:
При последовательном соединении пружин:
C |
C1C2 |
|
|
4 12 |
3 Н/ см = 3 0 0 Н/ м. |
|
C C |
2 |
4 12 |
||||
|
|
|
||||
|
1 |
|
|
|
Сила тяжести mg и реакция N представляет собой уравновешенную систему сил.
|
|
|
) 0. |
|
|
|
|
(mg, N |
|
|
|||
|
mx Fynp ; |
Fynp C , x ; |
|
|||
|
mx C(x ), |
|
|
|||
где С – |
жесткость пружины; |
|
|
|
|
|
(x ) – |
деформация пружины. |
|
|
|
|
|
|
mx Cx d sin pt m; |
|
||||
|
x C mx cd sin pt. |
|
||||
|
|
|
|
n |
|
|
Обозначим: C m k2 300 м/с2; Cd n |
300 0,04 |
12 м/с2 . |
||||
|
|
|
m |
1 |
|
|
114

Получим: x k2 x nsin pt – неоднородное дифференциальное уравнение II порядка. Решение этого уравнения:
x x0 x1 ,
где x0 c1 cos kt c2 sin kt Asin(kt ) – решение однородного дифферен-
циального уравнения (с1, с2 – постоянные интегрирования);
x1 Bsin pt – частное решение неоднородного дифференциального
уравнения;
x Asin(kt ) Bsin pt – решение неоднородного дифференциально-
го уравнения. Продифференцируем дважды:
x1 Bpcos pt; x2 Bp2 sin pt;
|
|
|
|
|
p2Bsin pt k2Bsin pt nsin pt. |
||||||||||||||||
B(k2 p2 ) n B |
|
|
n |
|
|
|
|
12 |
|
|
|
0,051 |
– |
амплитуда вынужденных |
|||||||
|
k |
2 p2 |
|
300 |
64 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
колебаний. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При t 0 |
|
|
|
|
|
|
|
|
|
|
|
x0 0; |
x0 0 . |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
x c1 cos kt c2 sin kt Bsin pt; |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 c1 0 0; |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c1 0. |
|
|
||
|
|
|
|
x k sin kt kc2 cos kt pBcos pt; |
|||||||||||||||||
|
0 kc |
pB c |
|
pB |
8 0,051 0,023 м; |
||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
k |
|
|
300 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A 0 |
|
|
|
|
|
x 0,05sin8t 0,023sin17,32t. |
|||||||||||||||
– амплитуда вынужденных колебаний, где – коэффициент |
|||||||||||||||||||||
динамичности. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 d. |
|
|
|
||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
1,27. |
||||
|
|
1 |
p |
2 |
/ k |
2 |
1 8 |
2 |
|
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
/ 17,3 |
|
|||||||||
|
|
|
|
|
|
|
A 0,04 1,27 0,0508 м. |
||||||||||||||
|
Tсв 2 / k 2 3,14 / |
|
300 0,363 c. |
||||||||||||||||||
|
|
|
Tвын 2 / p 2 3,14 / 8 0,785 c. |
||||||||||||||||||
x 5sin8t 2,3sin17,32t см – закон колебаний груза.
115
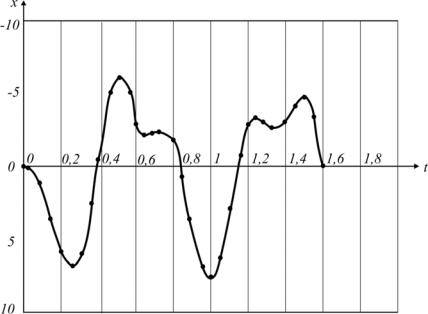
График колебаний представлен на рис. III.2.2.
Рис. III.2.2
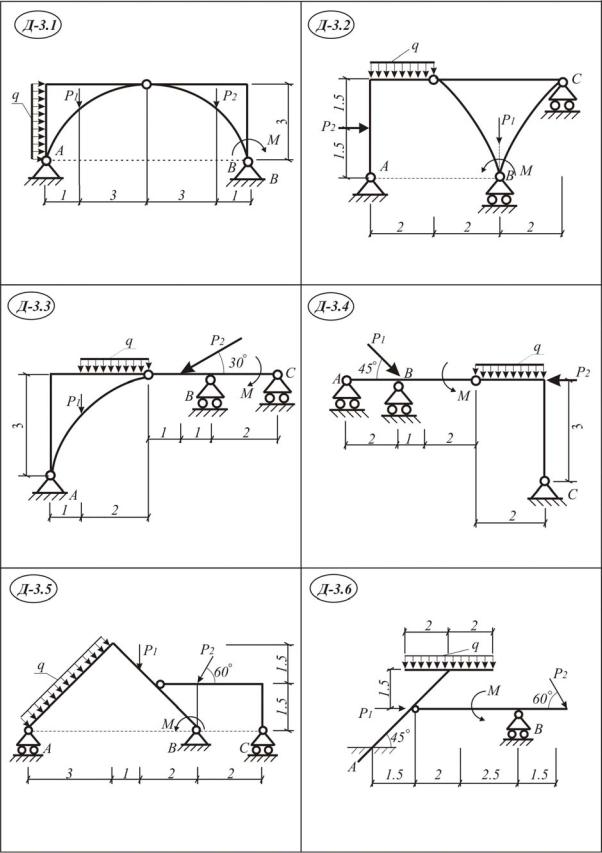
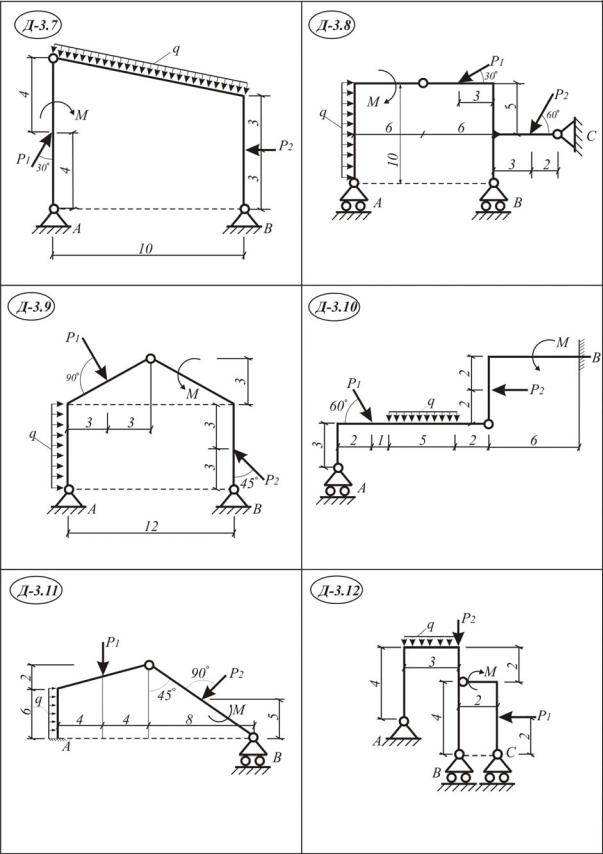
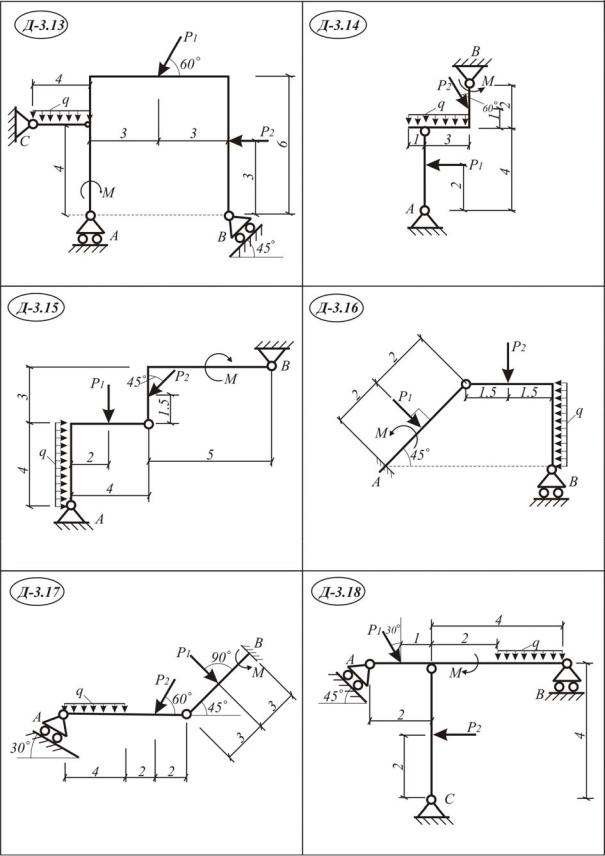
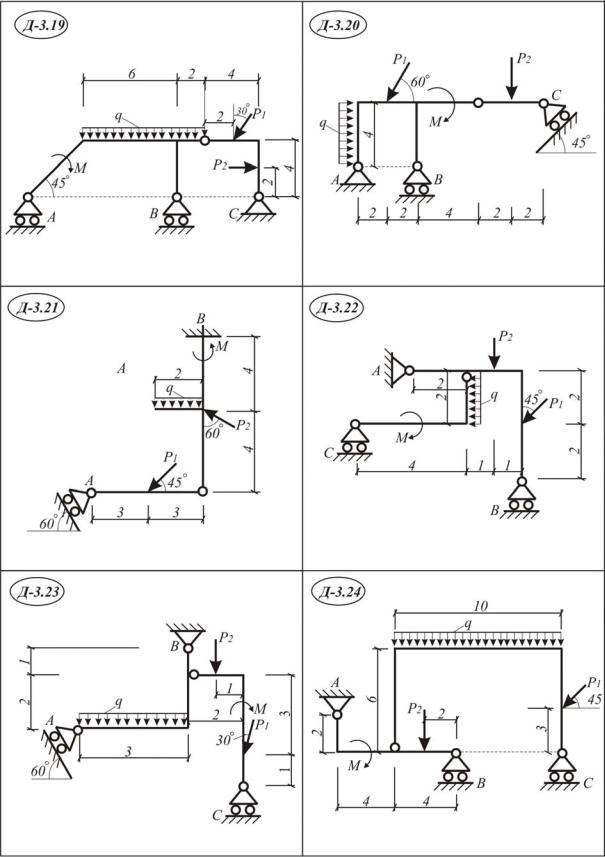
Задание Д3. Применение принципа возможных перемещений для определения реакций опор составных конструкций
Применяя принцип возможных перемещений, определить реакции опор составной конструкции. Схемы Д 3.1-30. Исходные данные приведе-
ны в табл. III. 3.1.
Таблица I I I . 3 . 1
Номер |
|
Нагрузка |
|
Номер |
|
Нагрузка |
|
||
|
|
q, |
М, |
|
|
Q, |
М, |
||
варианта |
Р1, кН |
Р2, кН |
варианта |
Р1, кН |
Р2, кН |
||||
|
|
|
кН/м |
кНм |
|
|
|
кН/м |
кНм |
1 |
15 |
14 |
3 |
10 |
16 |
3 |
10 |
2 |
10 |
2 |
13 |
12 |
2 |
6 |
17 |
1 |
8 |
1 |
8 |
3 |
11 |
10 |
1 |
5 |
18 |
3 |
6 |
3 |
6 |
4 |
9 |
8 |
3 |
14 |
19 |
5 |
4 |
2 |
7 |
5 |
7 |
6 |
2 |
12 |
20 |
7 |
2 |
1 |
5 |
6 |
8 |
5 |
1 |
4 |
21 |
10 |
9 |
2 |
4 |
7 |
7 |
4 |
2 |
10 |
22 |
8 |
7 |
1 |
7 |
8 |
6 |
6 |
1 |
7 |
23 |
6 |
5 |
2 |
8 |
9 |
5 |
8 |
3 |
8 |
24 |
4 |
3 |
1 |
3 |
10 |
4 |
10 |
2 |
6 |
25 |
2 |
1 |
2 |
2 |
11 |
12 |
11 |
1 |
12 |
26 |
7 |
1 |
2 |
7 |
12 |
10 |
6 |
2 |
10 |
27 |
6 |
2 |
1 |
5 |
13 |
9 |
5 |
1 |
6 |
28 |
5 |
3 |
2 |
10 |
14 |
7 |
10 |
2 |
13 |
29 |
4 |
4 |
1 |
5 |
15 |
6 |
8 |
1 |
5 |
30 |
3 |
5 |
2 |
10 |
116
117
118
119
120
