лаб1_Мансуров_3

МИНОБРНАУКИ РОССИИ

Санкт-Петербургский государственный

электротехнический университет

«ЛЭТИ» им. В.И. Ульянова (Ленина)

Кафедра Информационных систем (ИС)

отчет

по лабораторной работе №1

по дисциплине «Физика»

Тема: Исследование движения тел в диссипативной среде

Студент гр. 1324		Мансуров Я. В.
Преподаватель		Сизова Е. А.

Санкт-Петербург

2022

Цель работы.

Определение вязкости диссипативной среды (жидкости)

по установившейся скорости движения шарика в ней, а также исследование процессов рассеяния энергии в диссипативной среде.

Приборы и принадлежности.

Цилиндрический сосуд с жидкостью, металлические шарики, аналитические весы, масштабная линейка, секундомер.

Описание установки: цилиндрический сосуд, на боковой поверхности которого нанесены метки. Измеряя расстояние между метками и время движения шарика в жидкости между ними, можно определить скорость его падения. Шарик опускается в жидкость через впускной патрубок, расположенный в крышке цилиндра.

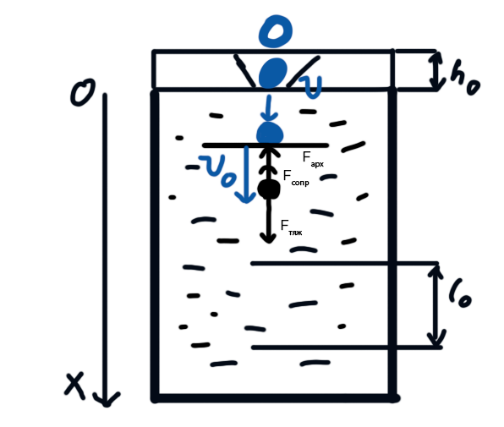
Исследуемые закономерности.

2. Сила сопротивления движению в водной среде , где - скорость движения тела, г – коэффициент сопротивления, зависящий от формы, размеров тела и от вязкости среды . Для шара радиуса R коэффициент сопротивления определяется формулой Стокса:

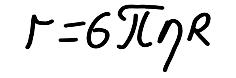
3. Д 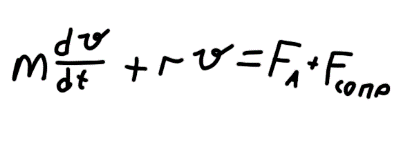вижение тела в диссипативной среде. Движение тела массой m под действием постоянной силы F при наличии сопротивления среды описывается след. уравнением:

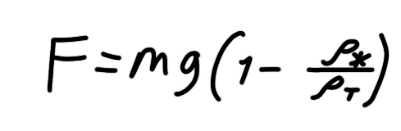, где и - плотности жидкости и тела соответственно. Таким образом уравнение движения преобразуется к виду:

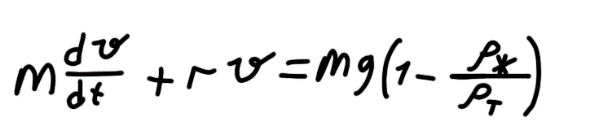
Обработка результатов эксперимента.

1. Рассчитаем значение коэффициента А:

A=9,81/6/3,14*(4*3,14*11,34/3)^1/3(1-1,25/11,34) =16,78 кг^1/3 / c²

2. По полученным данным вычислим значения установившейся скорости 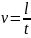для каждого шарика:

V_∞1=0,3/12,43=0,0241 м/с V_∞4=0,3/12,27=0,0244 м/с

V_∞2=0,3/19,34=0,0155 м/с V_∞5=0,3/23,59=0,0127 м/с

V_∞3=0,3/6,17=0,0486 м/с

Объёмы шариков 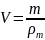: Радиусы

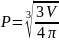
V₁=26*10^-6/11,34/10³=2,293*10^-9 м³ R₁=8,180*10^-4 м

V₂=12*10^-6/11,34/10³=1,058*10^-9 м³ R₂=6,321*10^-4 м

V₃=48*10^-6/11,34/10³=4,233*10^-9 м³ R₃=10,035*10^-4 м

V₄=24*10^-6/11,34/10³=2,116*10^-9 м³ R₄=7,964*10^-4 м

V₅=8*10^-6/11,34/10³=0,705*10^-9 м³ R₅=5,521*10^-4 м

Вязкость жидкости :

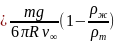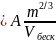
₁=0,610 Па*с ₄=0,571 Па*с

₂=0,567 Па*с ₅=0,528 Па*с

₃=0,455 Па*с

№	1	2	3	4	5
ni	0,610	0,567	0,455	0,571	0,528	n’=0,546
ni↑	0,455	0,528	0,567	0,571	0,610	R=0,155
Ui = ni+1 – ni	0,073	0,039	0,004	0,003	0,039	UP,NR=0,099
Δni = ni – n’	-0,091	-0,018	0,021	0,025	0,064	ΣΔn=0,001
(Δni)2*10-4	82,81	3,24	4,41	6,25	4,096	Σ(Δni)2=0,01008

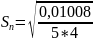=0,02245 Δn=t _{P, N} ∙ S_n=2,8*0,02245=6,286*10^-2 Па*с

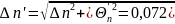
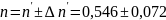Па*с

3. Для первого опыта рассчитаем коэффициент сопротивления r

r₁=6πn R₁=9,406*10^-3 кг/с

и мощность рассеяния P_d,

P_d1= 5,463 *10^-6 Вт

а также проверим баланс энергии на участке установившегося движения

Fl = P_dt =6,79*10^-5

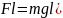) = 6,80*10^-5

Баланс соблюдается

4. Для первого опыта рассчитаем число Рейнольдса

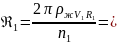0,254

Re₁<2300, т.е. движение слоёв ламинарное

5. Для первого опыта рассчитаем начальную скорость,

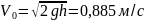
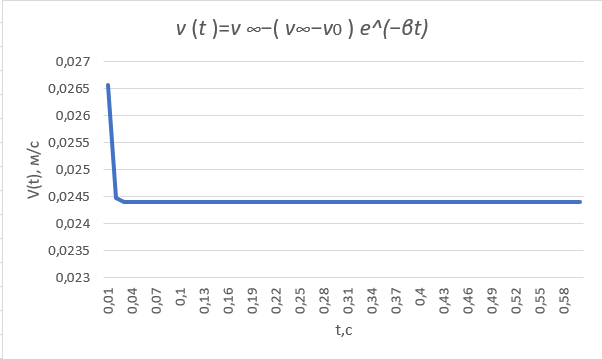
ускорение 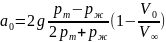=-22,084 м/с²

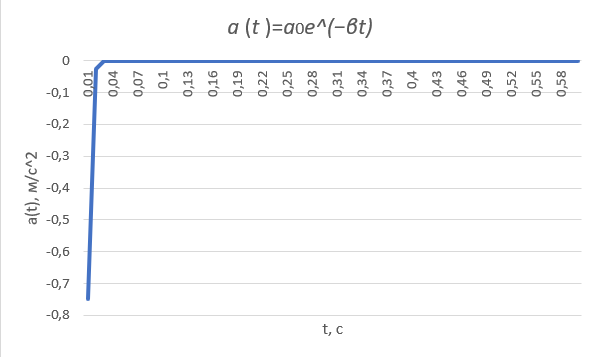
и время релаксации 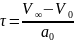=2,916*10^-3 c

6. Для первого опыта вычислим количество теплоты, выделяющееся за счёт трения шарика о жидкость, при его прохождении между двумя метками

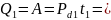6,79*10^-5 Дж

Вывод: Определена вязкость диссипативной среды (жидкости)

по установившейся скорости движения шарика в ней, а также исследован процесс рассеяния энергии в диссипативной среде.