Файловый архив студентов. Файловый архив студентов.
1302 вуза, 5135 предмета.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Пензенский Государственный Университет Архитектуры и Строительства
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

2394

.pdf
Скачиваний:
3
Добавлен:
17.06.2024
Размер:
8.35 Mб
Скачать
☆

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Пензенский государственный университет

архитектуры и строительства» (ПГУАС)

М.Б. Зайцев

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Сборник олимпиадных задач Часть II. Кинематика

Рекомендовано Учебно6методическим объединением вузов РФ по образованию в области строительства в качестве учебного пособия для студентов, обучающихся по программе бакалавриата

по направлению 08.03.01 (270800) «Строительство»

Пенза 2015

1

УДК 531.1 (075.8) ББК 22.21 я73

З617

Рецензенты: кафедра теоретической и прикладной механики Пензенского государствен6 ного университета (зав. кафедрой доктор технических наук, профессор В.В. Смогунов); доктор технических наук, профессор И.А. Прошин (ПГТУ)

Зайцев М.Б.

З617 Теоретическая механика. Сборник олимпиадных задач. Ч.II. Кинематика: учеб. пособие / М.Б. Зайцев. – Пенза: ПГУАС, 2015. – 92 с.

ISBN 978(5(9282(1302(2

Содержатся задачи по теоретической механике по разделу «Кинематика». Приводятся ответы к их решению.

Учебное пособие подготовлено на кафедре механики ПГУАС и предназначено для студентов, обучающихся по программе бакалавриата по направлению 08.03.01 (270800) «Строительство», углубленно изучающих теоретическую механику. Данное пособие можно использовать при подготовке к олимпиадам по теоре6 тической механике различного уровня.

© Пензенский государственный университет

ISBN 978(5(9282(1302(2 архитектуры и строительства, 2015 © Зайцев М.Б., 2015

2

ПРЕДИСЛОВИЕ

На кафедре «Механика» Пензенского государственного универси6 тета архитектуры и строительства из года в год ведется работа по под6 готовке студенческих команд для участия в предметных олимпиадах различного уровня. На внутривузовских олимпиадах выявляются наи6 более способные и талантливые студенты, обычно призеры универси6 тетских конкурсов, с которыми в дальнейшем проводятся дополнитель6 ные занятия по решению задач повышенной трудности.

Участникам олимпиад предлагаются обычно нестандартные задачи, для решения которых требуются не только твердые знания, но и оригинальность мышления.

Олимпиадное движение в деле организации научно6исследова6 тельской работы студентов, несомненно, является одним из ключевых компонентов.

Участие студентов в предметных олимпиадах способствует более глубокому усвоению дисциплин и формирует способность их к твор6 ческому освоению.

В данном учебном пособии содержится более 180 задач по теоре6 тической механике раздела «Кинематика». Многие из этих задач выда6 вались студентам в качестве конкурсных на различных универси6 тетских и региональных олимпиадах. Отдельные задачи заимствованы из работ, приведенных в списке литературы, часть из них составлена автором.

Настоящее пособие предназначено для студентов, углубленно изучающих теоретическую механику. Оно является тренировочным материалом для подготовки к олимпиадам по теоретической механике различного уровня.

Автор признателен ведущему инженеру6программисту Компьютер6 ного центра ИСИ Раевской Г.А. за помощь в оформлении данного пособия.

3

2y;

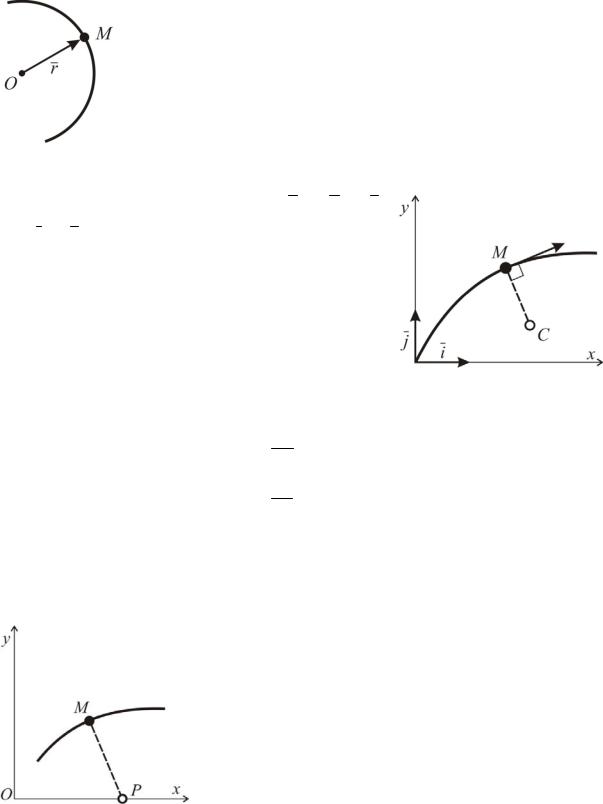
1.КИНЕМАТИКА ТОЧКИ

1.1.Задачи о движении точки

Задача К1

Точка движется в плоскости таким образом, что составляющая ее скорости, перпендикулярная к ра6 диусу6вектору OM, обратно пропорциональна величине этого вектора. Доказать, что ускорение точки M на6 правлено вдоль OM.

Задача К2

Тело движется со скоростью 2 ti 3 j , где i и j орты координатных осей. Найти скорость и ускорение центра кривизны траектории движущейся точки по отноше6 нию к указанной системе координат.

Задача К3

Точка движется в соответствии с уравнениями:

dxdt

dy 8x.

dt

При t=0 координаты точки x0=0; y0=4 см.

Определить зависимости скорости и ускорения точки от времени.

Задача К4

Движение точки М задано уравнениями x t sin t , y 1 cos t . Найти радиус кривиз6 ны траектории точки и доказать, что ρ=2 PM, если OP=t.

4

Задача К5

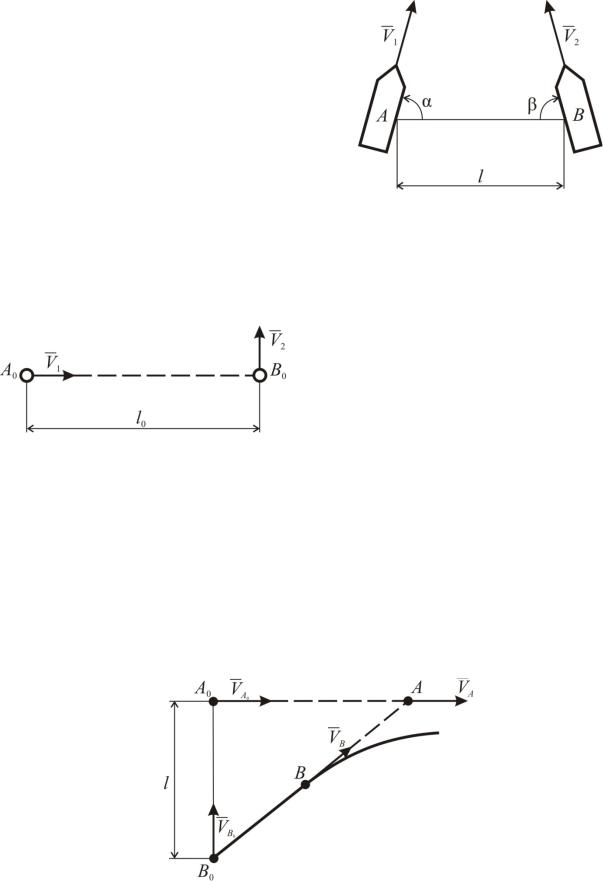
Два судна A и B, расстояние между которыми в начальный момент времени равно l, движутся пересекающимися курсами с постоянными скоростями V1 и V2 соответственно. Направления скоростей составляют углы α и β с прямой AB, на которой находятся суда в начальный момент времени. Найти наименьшее расстояние между судами при их движении.

Задача К6

Две точки A и B движутся по прямым, расположенным в одной плоскости, с постоянным скоростями V1 и V2. В начальный момент времени расстояние между точками равно l0, направления скоростей указаны на чертеже. Определить кратчайшее расстояние между точ6

ками A и B.

Задача К7

Точки A и B движутся в плоскости рисунка с постоянными скоростями V и 2V, соответственно. Точка A движется прямолинейно, а скорость точки B в каждый момент времени направлена в точку A. Определить путь, пройденный точкой A до встречи с точкой B, если в начальный момент времени расстояние A0B0=l, а скорости VA и VB взаимно перпендикулярны.

5

Задача К8

Человек получил задание в кратчайшее время добраться из пункта А, находящегося на острове, в пункт В на берегу, причем остров находится на

расстоянии 10 3 км от берега. В каком месте С человек должен пересесть с катера в автомобиль, если скорость автомобиля 72 км/ч, а катера 36 км/ч?

Задача К9

Лодку, уносимую течением реки, подтягивают к берегу веревкой с постоянной скоростью V. Определить уравнение траектории лодки, принимая ее за материальную точку,

если скорость течения реки U, длина веревки была перпендикулярна к берегу.

Указание: при решении задачи удобно использовать полярную систему координат.

Задача К10

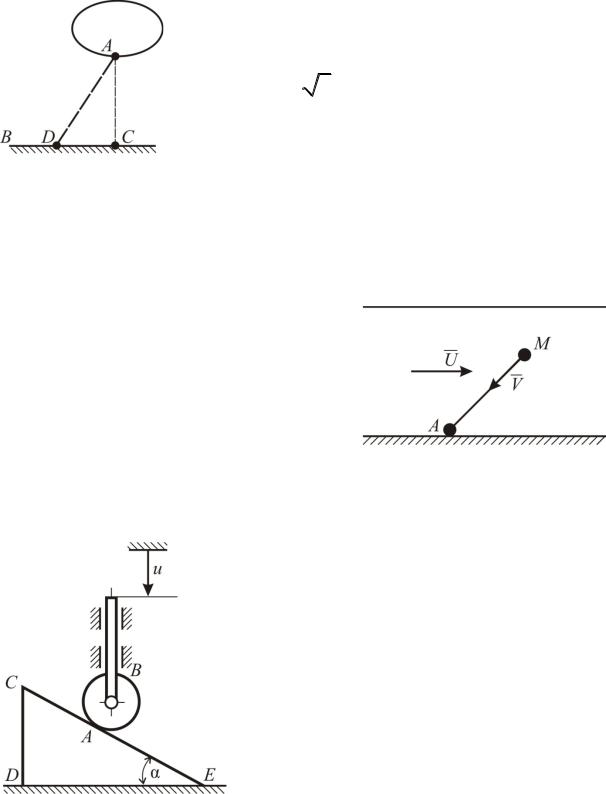
Стержень B движется в вертикальных направляющих по закону u(t)=bt3 и надавливает нижним концом на призму CDE. Найти скорость и ускорение призмы, если угол CED равен α. В начальный момент времени (t=0) CA=AE. Нижний ролик стержня В считать пренебрежимо малым.

6

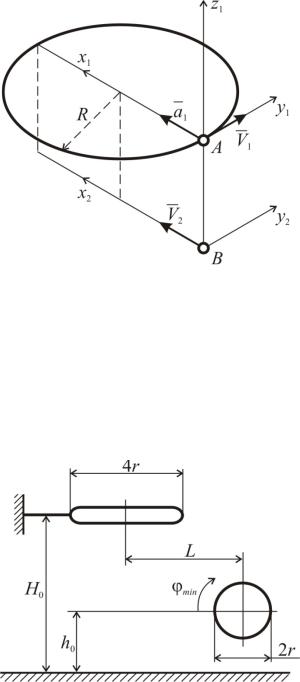
Задача К11

Автомобиль A двигается с постоянной скоростью V1 по кольцевой дороге радиусом R. Другой автомобиль B движется по радиальной автотрассе с постоянным ускорением a2. В тот момент, когда автомобиль A проезжает над шоссе, под ним проезжает автомобиль B со скоростью V2.

Определить, каковы в этот момент относительные скорости и уско6 рения автомобилей (относительно подвижных систем координат

Ax1y1z1 и Bx2y2z2).

Задача К12

Под каким наименьшим углом к горизонту φmin следует бросить баскетбольный мяч, чтобы он пролетел сверху сквозь кольцо, не ударившись в него. Толщиной кольца, изменением скорости мяча за время пролета через кольцо и сопротивлением воздуха пренебречь.

7

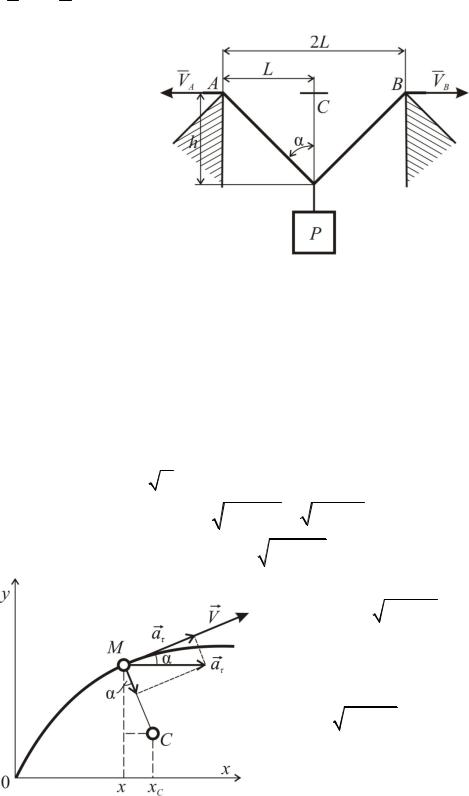
Задача К13

Груз P поднимается с помощью двух тросов, движущихся в противоположных направлениях с одинаковыми скоростями (V A V B ). Определить скорость и ускорение груза.

1.2. Примеры решения задач к гл. 1

Решение задачи К2

x 2t; y 3;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x t 2 C ; y 3t C

2

,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

при t=0 x

=0,

y

=0,

тогда

C

=0,

C =0

 

и

 

окончательно x=t2; y=3t,

0

 

0

 

 

 

 

 

1

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

траектория y 3 x есть парабола.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Модуль скорости V

x2

y2

 

4t 2 9 (м/с).

 

 

 

 

Ускорения x 2,

y 0, a

x2

y2 2 (м/с2 );

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a

 

 

dV

 

 

 

 

 

 

4t

 

;

 

 

 

 

 

 

 

 

 

 

 

 

τ

dt

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4t 2 9

 

 

 

 

 

 

 

 

 

 

 

 

a2

a2

 

a2

 

36

 

;

 

 

 

 

 

 

 

 

 

 

 

4t 2

9

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

 

 

τ

 

 

 

 

 

 

 

 

 

 

 

 

 

 

an

 

 

 

6

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4t 2 9

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Радиус кривизны

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

V

2

 

 

1

(4t 2

9)3/2.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a

 

 

6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

n

 

 

 

 

 

 

 

 

 

 

8

Из рисунка:

x x

sin ,

 

y

 

y cos , sin

an

,

cos

a

.

 

 

 

 

 

 

 

C

 

 

 

 

C

 

 

 

 

 

 

 

a

 

a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тогда x

t 2

 

1

(4t 2

9),

y

 

3t

t

(4t 2

9);

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C

2

 

 

 

C

 

 

3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x

2t 4t 6t, y

4t 2

; V

x2

y2

2t

4t 2 9;

 

 

 

C

 

 

 

 

C

 

 

 

C

 

C

 

C

 

 

 

 

 

 

 

x

6, y 8t; a

x 2

y2

2 16t 2 9.

 

 

 

 

 

 

C

 

C

 

 

C

C

 

 

C

 

 

 

 

 

 

 

 

 

 

 

 

Ответ:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

V 2t

4t 2 9, a

2 16t 2 9.

 

 

 

 

 

 

 

 

 

 

 

C

 

 

 

 

C

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Решение задачи К3

Продифференцируем уравнение заданной системы:

 

d 2 x

 

2

dy

,

d 2 y

 

8

 

dx

.

 

 

 

 

 

 

 

 

 

 

 

dt 2

 

dt

dt 2

 

 

 

dt

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Т.к.

 

dy

 

8x, то

d 2 x

 

 

16x;

 

 

 

 

 

 

 

 

dt

 

dt 2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Т.к.

 

dx

 

2y, то

 

d 2 y

16y.

 

 

 

 

 

 

 

dt

 

 

dt

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Окончательно получим:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

d

2

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

16x

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dt

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(*)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

d 2 y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

16y

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dt

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Решение 16го уравнения системы (*) имеет вид:

 

 

 

 

 

 

 

 

 

 

 

C1 sin 4t C2 cos4t;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

V

 

 

 

dx

4C cos4t 4C

 

sin 4t.

 

 

 

 

 

 

 

 

 

 

 

x

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dt

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

При t 0 x x0 C2 0;

Vx 4C1 2y0 8; C1 2;

Vx 8cos4t; ax dVdtx 32sin 4t;

9

Решение 26го уравнения системы (*) имеет вид: y C3 sin 4t C4 cos4t;

 

 

 

 

V

 

 

dy

 

4C

 

cos4t 4C

 

sin 4t.

 

 

 

 

y

dt

3

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

При t 0

y y0

4 C4

4; Vy 4C3

0 C3 0;

 

 

V

 

16sin 4t;

a

 

 

dVy

64cos 4t;

 

 

y

y

dt

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

V

64cos2 4t 256sin2 4t 8

cos2 4t 4sin2 4t ;

a

1024sin2 4t 4096cos2 4t 32

 

sin2 4t 4cos2 4t ;

Ответ:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

V 8 cos2 4t 4sin2 4t ; a 32

 

sin2 4t 4cos2 4t .

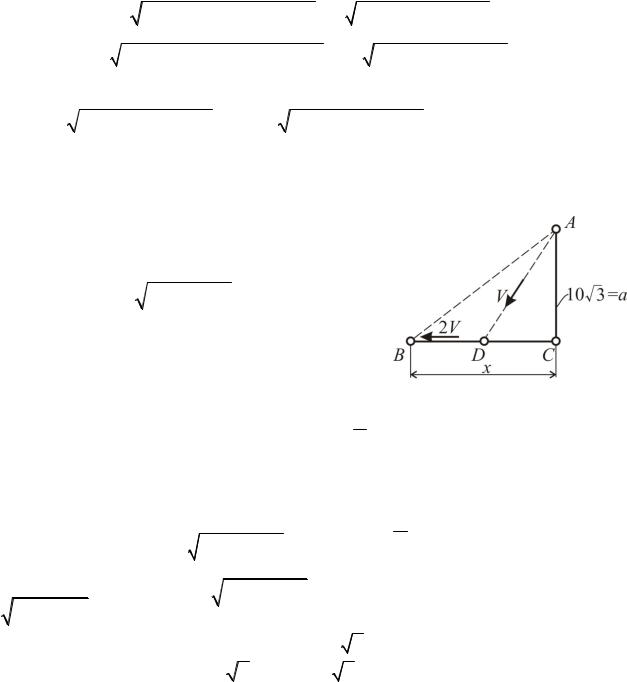
Решение задачи К8

BC

x

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

, DC x

?

 

Обозначим DC

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

BC

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a

2

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

AD

 

 

( x)

,

 

 

 

 

 

 

 

 

 

Тогда

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

BD x (1 )

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

следовательно, t t

 

 

t

 

 

 

 

AD

 

BD

.

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

V

 

 

2V

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

t

1

 

 

 

a

2

x

2

 

1/2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

V

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Т.к. t t( ),

то t t

min

 

при t' 0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ξ

 

 

 

 

 

 

1

 

1

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

t'

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(0 2(

 

 

 

 

 

 

 

 

 

2

 

 

 

2

 

V

 

2

 

 

 

 

a

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

( x)

 

 

 

 

 

x2 1 .

x) x (0 1) 0 2

2 x 2

 

 

 

 

 

 

 

 

 

x 0, 2 x a2 ( x)2 ,

 

4( x)2 a2 ( x)2 ,

3( x)2 a2,

 

a2 ( x)

 

 

 

 

 

 

 

 

 

x

a

,

1

 

 

10 3

 

10

.

 

 

 

x

 

 

 

3

 

3

 

x

 

Ответ: DC=ξ x=10 км.

10

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности