2388

Эллипс. Сумма расстояний от любой точки эллипса до двух фиксированных точек (фокусов F1, F2) есть величина постоянная. Наименьшее расстояние между двумя противоположными точками эллипса принято считать малой осью, наибольшее – большой осью. Малая и большая ось взаимно перпендикулярны и, пересекаясь, делят друг друга пополам.

Если даны фокусы эллипса, то построение его точек (М, К) показано на рис. 12. Делим расстояние между ними пополам, получаем точку О. Восстанавливаем перпендикуляр к прямой F1F2 и берем на нем произвольную точку А. При этом отрезок АО не должен быть больше отрезка FO. Сумма расстояний от токи А до точек F1F2 определит построение до любой другой точки эллипса. Множество полученных таким образом точек соединяются линейкой, которая называется лекалом.

Рис. 12. Построение эллипса с заданными фокусами

прямых принадлежат эллипсу, которые соединяют кривой линейкой (лекалом).

Парабола. Каждая точка параболы расположена на одинаковом расстоянии от фиксированной прямой f (директрисы) и от фиксированной

22

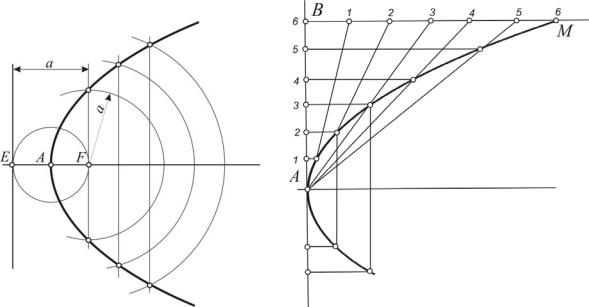
точки F (фокуса). Ось симметрии параболы проходит через ее фокус и перпендикулярна ее директрисе. Вершина параболы (точка А) делит отрезок FЕ на две равные части. Построение параболы, основанное на этом свойстве, показано на рис. 14. От вершины параболы на ее оси откладывают несколько отрезков, через которые проводят прямые, параллельные директрисе. На каждой из этих прямых располагаются по две точки параболы. Их расстояния от директрисы до фокуса равны.

Если заданы вершина параболы, некоторая ее точка М и направление оси, то построение остальных точек продемонстрировано на рис. 14. Из точки М проводят прямую, параллельную оси, из точки А – прямую, перпендикулярную оси. Эти прямые пересекаются в некоторой точке В. Отрезки АВ и ВМ делят на равное число частей, которые на каждом отрезке равны между собой. Дальнейшее построение видно из рис. 15.

Гипербола. Гиперболой называется плоская кривая линия, у которой разность расстояний от каждой точки до двух фиксированных точек F1, F2 (фокусов) есть величина постоянная и равная расстоянию между вершинами гиперболы (см. рис. 15).

Гипербола симметрична относительно двух взаимно перпендикулярных осей. Ось, которая содержит фокусы, называется действительной, другая ось – мнимой. Точка пересечения осей называется центром гиперболы. Прямые, проходящие через центр гиперболы и касающиеся ее в бесконечно удаленных точках, называются асимптотами.

23

На рис. 16 показано построение точек гиперболы, основанное на приведенном выше определении. В этом случае в качестве исходных элементов даны действительная ось, фокусное расстояние и вершины М1, М2.

Рис. 16. Построение гиперболы, основанное на свойствах ее точек

На действительной оси наносят точки, расстояние между которыми увеличивается по мере удаления от фокуса. Из фокусов проводят дуги радиусом, равным расстоянию от точки 1 до вершины М1 или М2 . Точки пересечения этих дуг принадлежат ги-

пербола, парабола и еще окружность образуют группу линий, которые на-

24

зываются кониками. Такое название они получили потому, что каждую из них можно получить в результате сечения прямого кругового конус плоскостью.

Если коника задана двумя касательными и тремя точками, что на практике бывает достаточно часто, точки этой кривой строят по алгоритму, представленному на рис. 18. Исходными являются точки А, В и С, касательные прямые m и n, пересекающиеся в точке D, и прямые а и b, которые соединяют точки А и В с точкой С. Последовательность графических построений отмечена цифрами. Первую прямую можно провести через точку А или точку В под любым углом. Последующие операции видны на рис. 18.

Рис. 18. Построение кривой второго порядка по трем точкам и двум касательным

25

Контрольные вопросы

1.Каким способом образуются прямые и кривые линии?

2.Что считается порядком кривой?

3.Какие кривые линии называются плоскими?

4.Какие кривые линии считаются пространственными?

5.Дайте определение лекальных кривых.

6.Дайте характеристику эллипсу.

7.Какая линия называется параболой?

8.Что такое гипербола?

9.Воспроизведите алгоритм построения плоских кривых второго порядка.

1.3. Поверхности

Особую группу геометрических множеств составляют поверхности. Самым распространенным способом образования поверхностей является кинематический. Сущность его сводится к следующему. Выделяется некоторая линия, которая, перемещаясь по заранее заданному закону, образует поверхность.

Наиболее распространенной является классификация, которая представлена в виде схемы на рис. 19. Основанием для деления поверхностей на линейчатые и нелинейчатые является возможность или невозможность выделения на ней прямой линии. Поверхности, на которых можно выделить прямую линию, называются линейчатыми. Если на поверхности невозможно выделить прямую линию, поверхность называется нелинейча-

той.

Способы образования поверхностей являются основанием для деления их на поверхности вращения и перемещения по направляющим. На схеме видно, что линейчатые и нелинейчатые поверхности могут быть образованы как вращением, так и другими способами.

Одной из важных характеристик поверхностей является их порядок. Порядком поверхности считается максимальное количество ее точек, общих с прямой, что соответствует порядку алгебраического уравнения, описывающего эту поверхность. Из всех рассмотренных выше поверхностей второй порядок имели цилиндрическая, коническая, призматическая, пирамидальная, а также сфера, эллипсоид, параболоид и гиперболоид. Остальные поверхности имели более высокий порядок.

Рассмотрим образование наиболее распространенных геометрических поверхностей. Зафиксируем в трехмерном пространстве точку Т и некоторую кривую линию f (рис. 20,а). Проведем через точку Т прямую l, которая пересекает линию f. Прямая l, перемещаясь в пространстве таким образом, что она скользит по линии f и проходит через точку Т, образует кониче-

26

скую поверхность. Прямая l называется образующей, точка Т – вершиной, кривая f – направляющей.

Рис. 19. Классификация поверхностей

В зависимости от характера направляющей и расположения вершины возникают следующие поверхности (табл. 2):

1)коническая – вершина Т на конечном расстоянии, направляющая f – кривая (рис. 20,б);

2)цилиндрическая – вершина Т бесконечно удалена, направляющая f – кривая (рис. 20,б);

3)пирамидальная – вершина Т – на конечном расстоянии, направляющая f – ломаная (рис. 20,в);

4)призматическая – вершина Т бесконечно удалена, направляющая f – ломаная (рис. 20,г).

Рис. 20. Образование класса конических поверхностей

27

Поверхности могут быть образованы вращением образующей вокруг оси i. Так возникают коническая (рис. 21,а) и цилиндрическая поверхности вращения (рис. 21,б).

Рис. 21. Образование поверхностей вращения (коническая, цилиндрическая)

Вместо прямой вокруг оси может вращаться и другая линия, например окружность или эллипс. При вращении окружности вокруг оси, совпадающей с одним из ее диаметров, образуется сфера (рис. 22).

28

Рис. 23. Образование гиперболоида, параболоида и эллипсоида

Контрольные вопросы

1.Охарактеризовать способ образования поверхностей.

2.Что называется образующей поверхности?

3.Какая линия играет роль направляющей?

4.Что такое вершина поверхности?

29

5.Какие поверхности называются линейчатыми?

6.Какие поверхности называются нелинейчатыми?

7.Что такое порядок поверхности?

8.Какие поверхности называются поверхностями вращения? Привести примеры?

9.Как образуются поверхности, принадлежащие к классу конических? Перечислить эти поверхности.

30