Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2381

.pdf

Скачиваний:

Добавлен:

17.06.2024

Размер:

8.13 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 178 9 10 11 12 13 14 15 16 17 > Следующая >>>

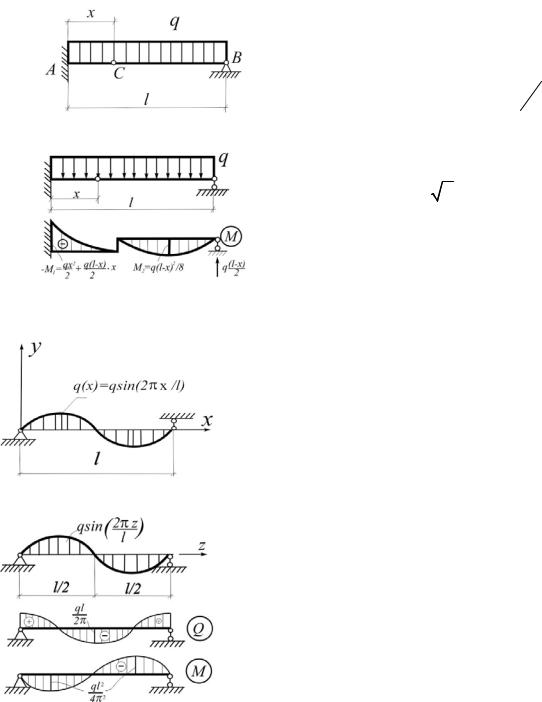
4.17. Определить положение шарнира С, при котором балка постоянногопоперечногосеченияобладаетнаибольшейгрузоподъем-

ностью (рис 4.17).

Решение

l x 2

l x

;

Рис.4.17

l x

0 1

4 1 2 , 2 6 1 0

5,83

0,17

Ответ:

x 0,17 l

Рис.4.17(а)

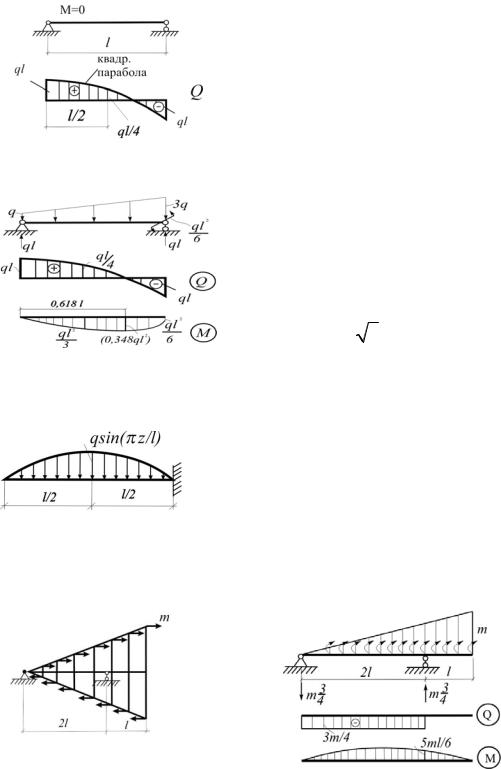
4.18. Построить эпюры Q и М (рис.4.18).

Решение

q z dz

2 z

1 cos

2 z

M Qdz

sin

Q0 z M0

Рис.4.18

M 0 0 :

M l 0 : 0 ql2

Q l, Q

Q z

cos 2 z

2 z

M z

sin

Рис.4.18(а)

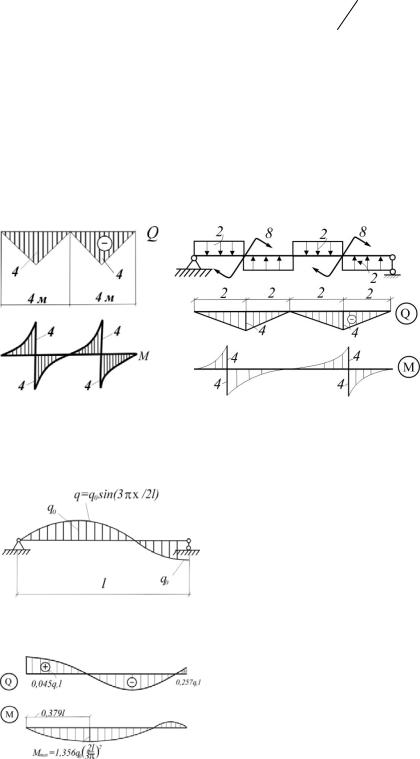
4.19. По известной эпюре Q для балки на двух опорах воспроизвести нагрузку и эпюру М, если известно, что распределенная и сосредоточенная моментная нагрузка в пролете отсутствуют, а изгибающий момент на левом конце балки равен нулю (рис.4.19).

Решение

Рис.4.19

Рис.4.19(а)

Q R :

R ql;

ql qz

;

Q z

M z Q z dz qlz q

;

l 3

q 2

;

q z

M z M

max

, если Q z

0 :

z 2

1,618

0,618

, 0

При z =0,618l: M z M max 0,348ql2 .

4.20. Написать выражение для Q и М в сечении z (рис. 4.20).

Решение

z l

qsin

dz q 1

cos

Рис.4.20

z l

M Qdz q z

sin

4.21. Построить эпюры Q и М для балки, загруженной изменяющейся моментной распределенной нагрузкой (рис.4.21)

Рис.4.21

Рис.4.21(а)

Решение

m3l

;

Q m

z 2l

z 3l

dm 3m z m

3m z 2l

3l 2

z 2l

z 3l

4.22. Указать нагрузку, приложенную к балке на двух опорах, по заданным эпюрам Q и М (рис. 4.22).

Решение:

dQ qdz

Mi Mi

Рис.4.22	Рис.4.22(а)

4.23. Найти реакции опор. Построить эпюры внутренних усилий

Q и М. Найти Mmax (рис.4.24).

Решение

qdz q0

3 z

1 cos

3 z

M Qdz q0

sin

Q0 z M0

Рис.4.24

M 0 0 : M

M l 0 : Q q

Q z q

cos 3 z

;

sin 3 z ;

M z q

Рис.4.24(а)

3 3

Q R : R

1 0,257q l,

0,045q l;

3 3

Q z 0 :

cos 3 z ,

z 0,379l,

1,356q

2 .

max

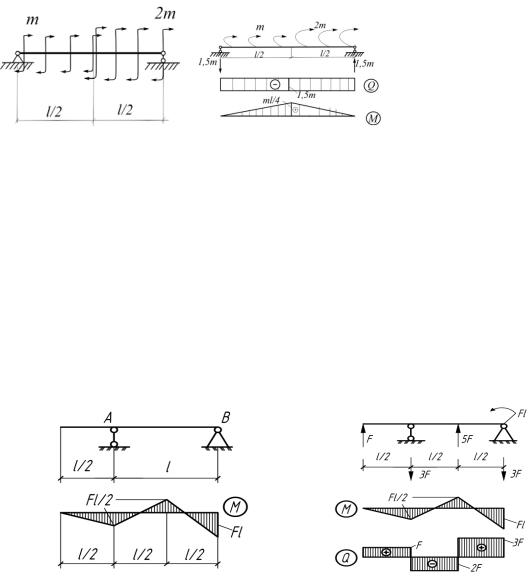
4.24. Построить эпюры Q и М для заданной балки. Объяснить, почемувэтомслучаенесоблюдаетсядифференциальнаязависимость

Q = dM/dx (рис.4.25).

Решение dMdz Q m

Рис.4.25 Рис.4.25(а)

1,5m;

M z 1,5mz mz z l/2

m z

z l/2

4.26. По заданной эпюре M установить нагрузку , действующую на балку , определить опорные реакции и построить эпюру Q (рис.4.26).

Рис.4.26 Рис.4.26(а)

Решение

а) Q dM

M к M н

; Q

;

/ 2

l / 2

б) M i M i :

M B Fl;

Qj Qj : RA 3F, RB 3F.

4.27. Найти x из условия равнопрочности стержня и балки, выполненных из одинакового материала (l/a=18) (рис.4.27).

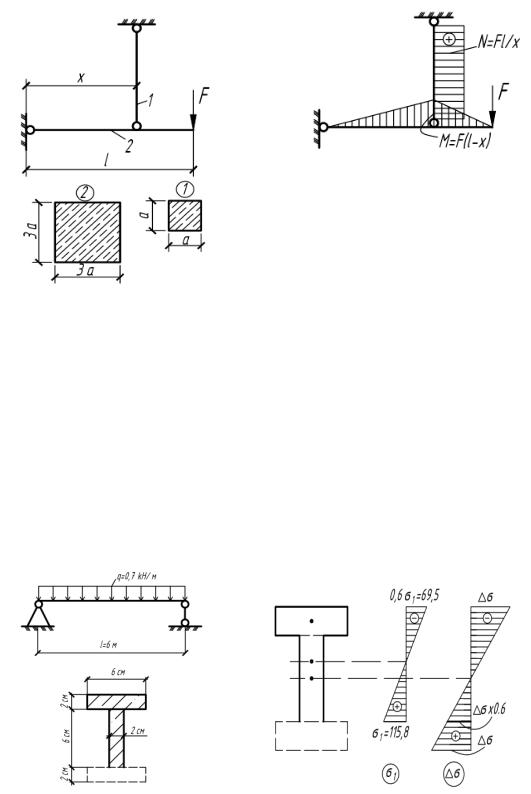
Рис.4.27

Решение

Рис.4.27(а)

а) из равновесия: M 0 :

;

F l x

x 2

б) по условию:

Fl / x

3a 3 / 6

Ответ: x=l/2.

4.28. Балка таврового сечения была нагружена распределенной нагрузкойq=0,7 кН/м. Затем, неснимая нагрузки, книжнейчасти сечения был приварен лист того же материала (на рисунке он незаштрихован). Определить, на сколько процентов можно будет увеличить нагрузку q после усиления сечения (R= 200МПа) (рис.4.28).

Рис. 4.28

Решение

Рис.4.28(а)

а) от q 0, 7

y 3 см, y

кН/м:

max

3,15 кНм;

5 см;

2 63

6 23

12 22

136 см4 ;

3,15 кНм 5 см

115,8 МПа ;

136 см4

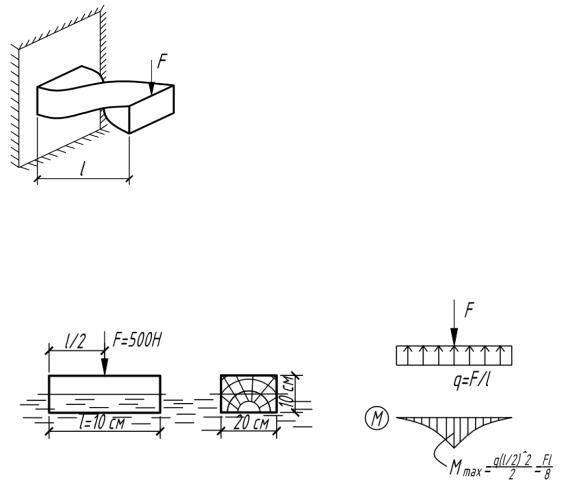
б) от q : M max

q l2

yв yн 5 см;

6 103

4 63

428 см4 , W 428

85,6 см3 ,

Mmax ;

в) от q2 q1 q :

max R :

0,6 σ1 σ 200,

130,5,

σ1 0,6 σ 200,

σ 140,3;

тогда σ 130,5 МПа :

max

W 130,5 МПа 85,6 см3

11,17 кНм,

Mmax

11,17

3,55 . Ответ: на 355%.

max

3,15

4.29. Определить прогиб на концевитой балкиквадратного сечения b b. Дано: F, E, b, l (рис.4.29).

Решение Для квадрата:

Ix Iy b4 const : 12

max	Fl3	4Fl3
	3EIx	Eb4

Ответ: 4Fl3 .

Рис. 4.29

Eb4

4.30. Определить нормальные напряжения в опасной точке поперечного сечения для плавающего прямого бруса, нагруженного в середине. Изменением формы бруса пренебречь (рис.4.30).

	Рис. 4.30			Рис.4.30(а)
			Решение
max	Mmax	Fl / 8	3Fl	3 500 Н 10 м	1,875 МПа.
	Mmax	bh2 / 6	4bh2	4 20 см (10 см)2	1,875 МПа.
	W	bh2 / 6	4bh2	4 20 см (10 см)2
	x

Ответ: 1,875 МПа.

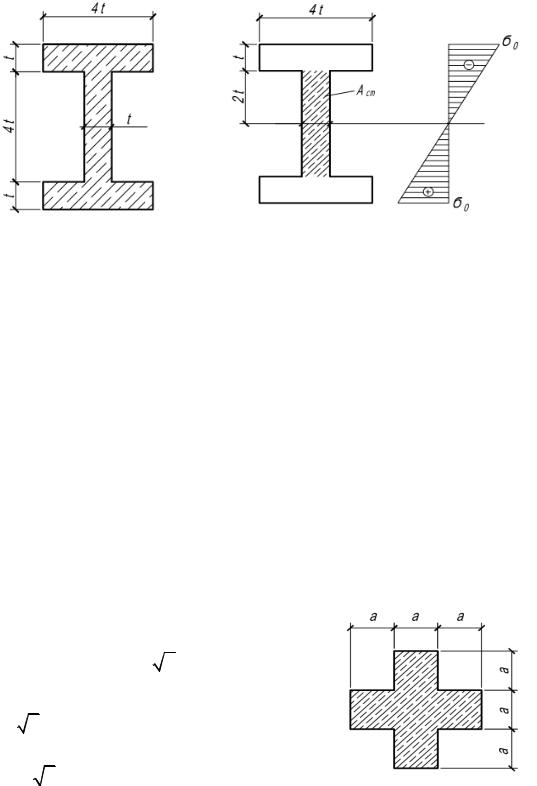
4.32. Двутавр изгибается в вертикальной плоскости. Определить доли изгибающего момента и поперечной силы, воспринимаемые материалом стенки и полок двутавра (рис.4.32).

Рис. 4.32 Рис. 4.32(а)

Решение

а) Ix

4t 6t 3

3t 4t 3

56t4

Iст

t (4t)3

16 t4 ,

10,5;

Iст

M y :

Mст dAy M Iст 0,095M ,

Mп M Mст 0,905M ;

Aст

Q Sxотс

Q 12t2 0,5 y2 t

Qt4

б)

: Qст dA

tdy

0,81Q

56t

Aст

Ответ: Mст 0, 095M ,

M п

0, 905M ; Qст

0, 81Q,

Qп 0,19Q.

4.34. Балка заданного сечения подвергается изгибу в двух вариантах: в плоскости вертикальной оси симметрии и в плоскости наклонной оси симметрии. Определить отношение максимальных нормальных напряжений при этих вариантах (рис.4.34).

Решение

Ix	Iy I const :
		M 1,5a,		2	M 2a;
1		I			I
1
		1,5	1,06 .
2		2

Ответ: 1,52 1,06.

Рис. 4.34

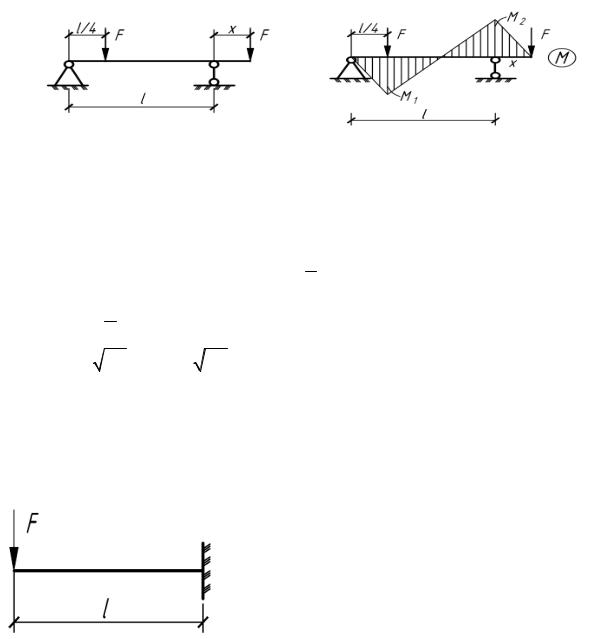
4.35. На каком расстоянии x следует установить правую опору, чтобы прочность балки по нормальным напряжениям была наибольшей? (рис.4.35)

Рис. 4.35

Рис. 4.35(а)

Решение

					3l
M 0 : RA l x Fx F					4
B					4
M1 M 2 :	RA	l	F x,	3l	2x

		4		4
		4		4

Пусть xl , где 0 1, тогда

			F	3l
x	0,	RA		4	2x	;

			l x

l l x x.4

2 1,5 0,1875 0,

	1,5	1,5	1,5 1,5 .
	2		2

Ответ: x 0,138l.

4.36. Консольная балка прямоугольного сечения площадью A изгибается силой, приложенной на ее свободном конце. Указать , как с помощью тензометра , наклеенного на балку , определить модуль сдвига материала балки (рис.4.36).

Решение

В поперечном сечении на нейтральном

слое:

3 F

max

: это чистый сдвиг,

2 A

max ; 45 .

т.е. 1

max ;

Рис. 4.36

max 1 max 1,5F / A

Ответ: G

, где ε1

измеряется на нейтральном слое под =45 .

4Aε1

4.37. Определить размеры h и a таврового сечения балка из условия её равнопрочности по , если Rсж = 90 МПа, Rр= 30 МПа.

Балка испытывает чистый изгиб (М= -0,18 МН м) (рис.4.37).

Рис. 4.37 Рис. 4.37(а)

Решение Нейтральная ось x на границе полки со стенкой:

0 : R

a h 2a

2a 9a ,

2 9a

2a 8a.

сж

Rсж / Rр

9a (2a)3

a (h 2a)3

96a4 ;

max M 2a Rр, a 3

0,18 МНм

5 см,

h 8a 40 см.

48 Rр

48 30 МПа

Ответ: h=40 см, a=5 см.

4.38. Вывести приближенные формулы для и при изгибе

двутавровой балки, если расстояние между центрами тяжести поясов площадью A1 и A2 и высота стенки толщиной t приняты равными h.

При вычислении статического момента и момента инерции не принимать во внимание сечение стенки, а сечения поясов считать сосредоточенными в их центрах тяжести. Считать, что М воспринимается только поясами, а Q – только стенкой (рис.4.38).

Решение Положение нейтральной оси x:

A A A

A2 h

A1 h

A y2

A1 A2

h2 .

1 1

2 2

M y

;

A1 h

A2 h

Q Sотс

Q A A

h t

Ответ: σ1

σ2

;

A1 h

A2 h

h t

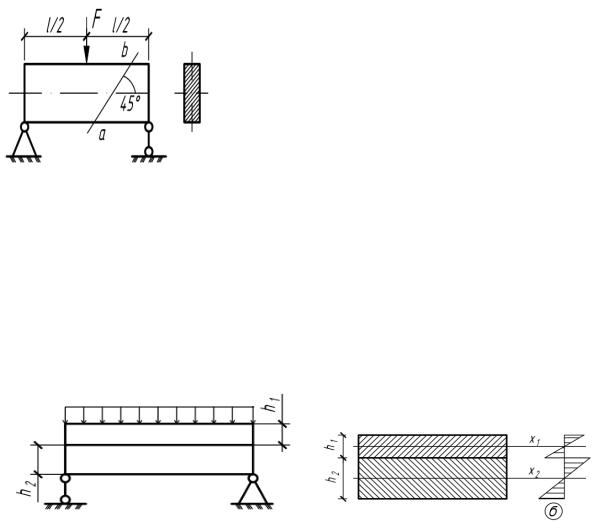
4.39. Вточкенейтральногослоябалкипрямоугольногопоперечного сечения замерена линейная деформация в направлении линии ab:

εab 0,5 10 4 . Определить модуль сдвига материала балки, если площадь поперечного сечения A = 10 см2 , а сила F= 20 кН.

Решение

В поперечном сечении на нейтральном

слое:

F / 2

max

: это чистый сдвиг,

45 .

т.е. 1

max ; 3

max ;

max 1 max 1,5F / A

3 20 кН

150 ГПа.

8 10 см2 0,5 10 4

Ответ: G 150 ГПа.

4.40. Две лежащие одна на другой доски несут равномерно распределенную нагрузку. Показать, что наибольшие нормальные напряжения будут пропорциональны толщинам досок, если трением между досками пренебречь (рис.4.40).

Рис. 4.40 Рис. 4.40(а)

Решение

где M M1 M 2 ,

I I1

I2 :

M I1

M 2

M I2

;

M1 h1

M h

;

2max

M2 h2

M h .

1max

2I 1

2I 2

M h

M h .

Ответ: σ

;

1max

2I 1

2max

<<< < Предыдущая 1 2 3 4 5 6 78 / 178 9 10 11 12 13 14 15 16 17 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.06.20248.07 Mб02377.pdf
#
17.06.20248.08 Mб02378.pdf
#
17.06.20248.08 Mб02379.pdf
#
17.06.2024243.89 Кб0238.pdf
#
17.06.20248.09 Mб02380.pdf
#
17.06.20248.13 Mб62381.pdf
#
17.06.20248.16 Mб02382.pdf
#
17.06.20248.23 Mб02383.pdf
#
17.06.20248.23 Mб02384.pdf
#
17.06.20248.23 Mб42385.pdf
#
17.06.20248.24 Mб02386.pdf