Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2381

.pdf

Скачиваний:

Добавлен:

17.06.2024

Размер:

8.13 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 177 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

3.47. Для сечения в виде ромба определить, при каких соотношениях h/b будут максимальными Ix. Wx . Сторона ромба равна а (рис.3.47).

															Решение
																																		b										a
																											h
															a2												h															1					2
h	2	b		2	a		2		b	2					a2																											1
								,										,									b			;																				.							Рис.3.47
								,				1			2			,									b			;												a								.							Рис.3.47
												1			2																											a
																				0												h									1				2
																																									1
																	2b h3								bh3								b4 3										a4								3
										Ix					2				12							3									3									3												;
										Ix					2				12							3									3									3								2		2		;

																																																1
																		Ix Imax ,											если									I 'x 0 :
																		Ix Imax ,											если									I 'x 0 :
																3 2 1 2 2 3 2 1 2 2
													a4			3 2 1 2 2 3 2 1 2 2																																			0,
													a4																																						0,
														3																		2				4
														3														1				2				4
																												1
														3 1 2 4 2 0,																					2 3,										3 .
															W							Ix					bh2						a3											2
															W												bh2						a3
																		x				ymax							3								3									2

																																										1							3/2
															W W																											1
															W W													,	если W ' 0
																		x					max																	x
																		x					max																	x
									a3						2 1 2 32 2																							23 1 2 12 2
									3																																														0,
									3																						2				3																				0,
																												1
															2 1 2 3 2 0, 2 2, 2 .
			Ответ:						h			3 для I									x	I		max					;	h									2 для W										x		W		max				.
									b												x			max						b																			x				max
			3.48. При каком соотношении a/h момент со-
противления сечения относительно оси z																																												не изме-
нится при повороте оси на 450 (рис.3.48)?
															Решение
h			h		2				a		2												2											2						a																	Рис.3.48
2			2		2				2		2			,			h 1						2				a					2					,			h						2					1 .						Рис.3.48
2			2		2				2		2												2									2								h
	Ответ:					a					2 1 .
	Ответ:					h					2 1 .

3.49. При каком соотношении размеров крестообразного сечения наличие верхнего и нижнего ребер приводит к уменьшению момента сопротивления сечения относительно оси сим-

метрии z (рис.3.49)?

Рис.3.49

Решение

t h

/ H

bh2

b t h3

tH 2 ,

b b t

t H

Ответ:

3.50. Двутавровое сечение получается присоединением к прямоугольнику ABCD прямоугольников EFGH и KLMN. При какой ширине х добавляемых прямоугольников момент сопротивления сечения увеличится в два раза

(рис.3.50)?

Решение

Рис.3.50			Wx1 th2					;
						6
			W		2
				x			2 :
							2 :
				W	1
				x
Ответ:	x	h3	4t h				.
Ответ:	x	2t2 6 h t 2					.
		2t2 6 h t 2

				2							3			t h		3
W 2				2			x h 2t					x		t h			.
W 2		h			2t							x		12			.
	x	h			2t				12					12

2					h 2t			3	h	3	th		3	th	2
2			x		h 2t				h						.
			x												.
	h 2t					12					12			3
	h 2t					12					12			3

3.52. Определить размеры прямоугольника, который можно выделить из равнобедренного треугольника так, чтобы момент сопротивления прямоугольника относительно центральной оси, параллельной основанию, был максимальным

Рис.3.52 (рис.3.52).

Решение

B b

H h

;

h H x .

1 x

;

1 x 3

3 x2

2x 1

;

1 x

Wx' 0 :

2 1 x 3x 0, x 2 :

Ответ: b B3 ; h 23 H.

Задачи для самостоятельного решения

3.1. Определить осевой момент инерции Ixо сечения, показанного на рис.3.14.

Ответ: 6, 274r4.

3.2. Вычислить центробежный момент инерции полукруга относительно осей x, у.

Ответ: 23 r4.

3.18. Найти центробежный момент инерции Ixу четверти круга.

Ответ: Ixy r84 .

3.18. Найти осевой момент инерции треугольника ABC относительно оси x, если известны координаты его вершин:

А(0,0), B(b,2b), С(2b,b) (рис.3.20).

Ответ: Ix 1,75b4.

3.18. Для заданной несимметричной фигуры определить момент инерции относительно оси x.

Ответ: Ix 10a4.

3.40. При каком соотношении h/b все оси, проходящиечерезсерединуоснования равнобедренного треугольника (точка С), будут главными.

Ответ: hb 12 .

3.51. В прямоугольном сечении одно квадратное отверстие стороной а заменено двумя квадратными отверстиями со стороной х, как показано на рисунке. Определить х из условия, что моменты сопротивления обоих сечений одинаковы.

Ответ: x 4 a26 .

Глава 4. ПЛОСКИЙ ПОПЕРЕЧНЫЙ ИЗГИБ (УСИЛИЯ И НАПРЯЖЕНИЯ)

Краткие теоретические сведения Основные понятия и обозначения

X ,Y соответственно нейтральная ось и силовая линия, совпадающие с главными центральными осями поперечного сечения стержня;

q q z погонная распределенная поперечная нагрузка; qz qz z погонная продольная сдвигающая нагрузка; m m z погонная распределенная моментная нагрузка;

Qy Q z поперечная сила в поперечном сечении стержня;

M x M z изгибающий момент в поперечном сечении стержня;

балка стержень, испытывающий деформацию изгиба, т.е. изгибаемый; консоль стержень или его часть, между свободным концом и закреплением; пролёт стержень или его часть, между закреплениями;

а) правила знаков: z, qz 0 : ;	q 0 : ;	m 0 : ;
,Q 0 : ;	M 0 : ;

б) дифференциальная зависимость внутренних усилий от внешней нагрузки:

dQ	q,	dM	Q m;
dz		dz
в) правила о скачках: Q F,		M M ;

г) напряжения в произвольной точке поперечного сечения стержня:

M x y для сплошной однородной балки ,


		E		M x		y для сплошной композитной балки ;
		E				y для сплошной композитной балки ;
	i	i	EIпр
dM					Sxотс		без учета сдвигающей нагрузки qz ,
dM					Ix by		без учета сдвигающей нагрузки qz ,
		dz			Ix by

	в	н	в	н	2 y
by	qz	qz	qz	qz	2 y	dM
by		2		2	h	dM
		2		2	h	dz

Sотс		h	н		h	в
x	где		qz	y		qz	;
Ix	где	2	qz	y	2	qz	;
Ix		2			2

в наиболее удаленных точках сечения от нейтральной оси, при y ymax :

0,	max M x ymax M x это линейное напряженное состояние;
	Ix	Wx
на нейтральной оси, при y 0 :			max ,	0 это чистый сдвиг;

в) условие прочности материала стержня:

расчетное по при y ymax :	max R,
проверочное по при y 0 :	max Rs ,

г) условие равнопрочности сечения: Rр

р,max

где	max	Mmax		;


		Wx
		Wx	Sп.с
		Q
		Q
где	max	max		x	;
		max		x

		Ix by

Rс .

с,max

Примеры решения задач

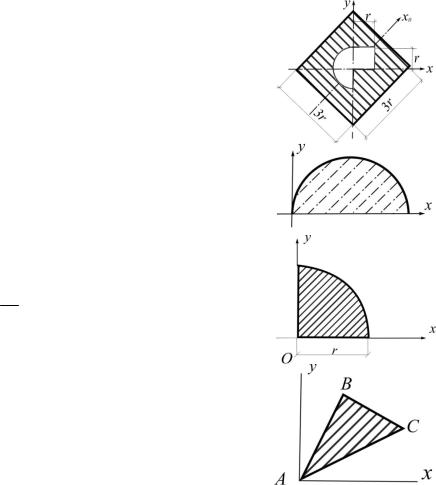
4.1. Балка загружена распределенной нагрузкой q( z )=q0sin(πz /l). Построить эпюры поперечных сил и изгибающих моментов (рис.4.1).

Решение

z l

2RA 2RB q0 sin

dz q0

cos

;

Рис.4.1

Q q z dz q0

cos

M Qdz q0

sin

Рис.4.1(а)

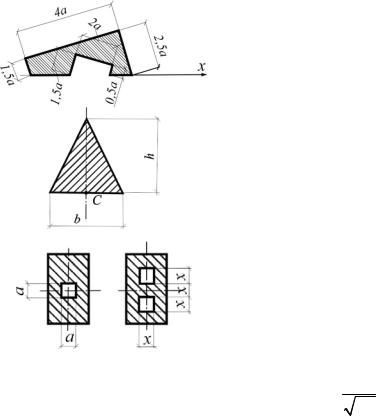
4.2. Найти наиболее невыгодное положение тележки крана на

балке (х), при котором возникает наибольший изгибающий момент. Вычислить величину наибольшего момента. Давление на каждое колесо Р (рис.4.2).

Решение

l x a / 2 ;

x a / 2

2P l x a / 2

M1 RAx

Рис.4.2

R l x a 2P l x a x a / 2

		x 0 :
M1'		x 0 :	l 2x a / 2 0,

				a
	'	x 0 :		a	l x a ,
M2		x 0 :	x		l x a ,
				2
		l / 2 a / 4			, Mmax
Ответ: x				3a / 4	, Mmax
		l / 2		3a / 4

l a / 2

l a / 2 2

;

l 3a / 2

2P l a

/ 2 2

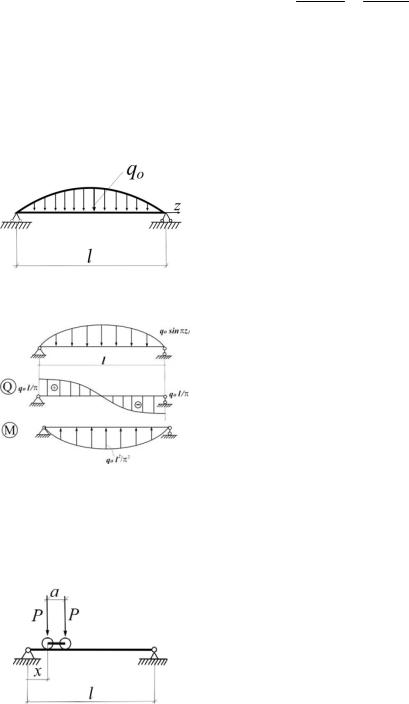
4.3. Как должна изменяться ширина поперечного сечения балки b(х) при постоянной высоте h, чтобы изогнутая ось балки была дугой окружности радиуса R (рис.4.4).

Решение

const

M Fx

b x h

12,

b x h3

Рис.4.4

Ответ: b x

12x.

Eh3

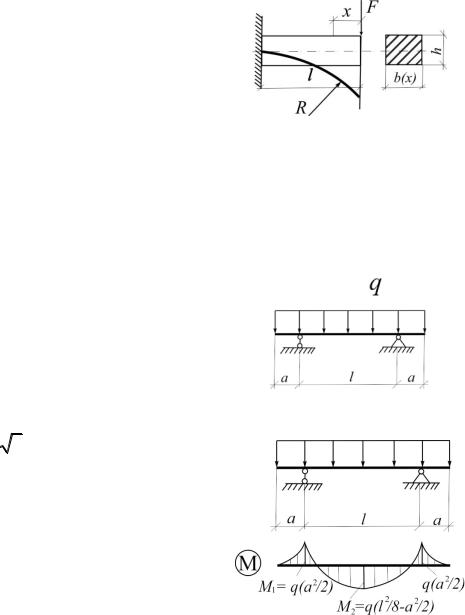
4.4. Определить положение опор (соотношение вылета консолей и пролета) балки постоянного сечения из условия минимума объема балки. Rсж = Rраст. (рис.4.5).

Решение

			M1 M2 :
q a		2				2	a	2	,
q a			q l				a		,
2					8		2
				2		l2			Рис.4.5
			a			8 .			Рис.4.5
			a			8 .			q
	l		2						q
Ответ: a	l		2	.
Ответ: a		4		.
		4

Рис.4.5(а)

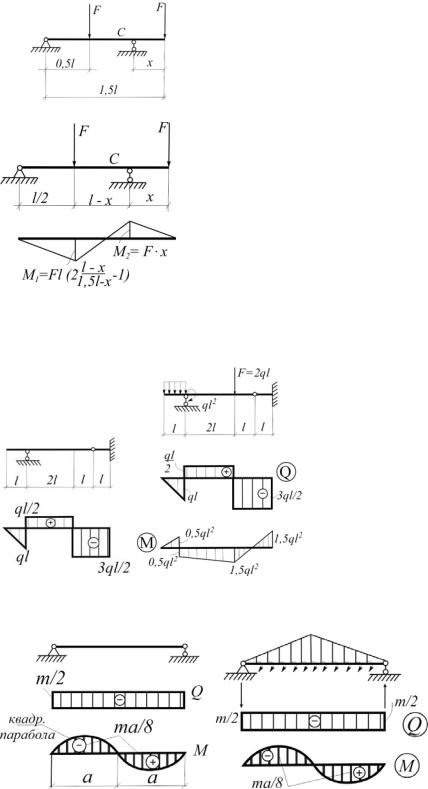
4.6. Где следует установить опору С, чтобы балка обладала наибольшей грузоподъемностью из условия прочности по нормальным напряжениям? (рис.4.6).

		Решение
			M1 M2 :
	0,5l x				0 1,5 ;
Fl	0,5l x		Fx			x
Fl	1,5	x	Fx			x

						l
Рис.4.6						l
0,5		,		2 2,5 0,5 0,
1,5
				2, 28			, 0,22
2,5 2,06							, 0,22
		2		0,22

Ответ: x 0,22l.

Рис.4.6(а)

4.7.По эпюре Q определить нагрузку на балку и построить эпюру

М(рис.4.7).

Решение

Qi Fi ;

	dQ	q,	dM Q ;
	dz		dz
		M лев 0 :
		c
	q l 3,5l 2ql l 1,5ql 3l M 0 ,
		M ql2 .
Рис.4.7	Рис.4.7(а)
4.8. Определить нагрузку на балку по эпюрам Q и М (рис.4.8).
			Решение
		dM Q m ;
			dz
			dz
			dQ	q :			q 0;
			dz	q :			q 0;
			dz		m		m z
		M			m	z2
		M			2a	z2
Рис.4.8	Рис.4.8(а)				2a		2
Рис.4.8	Рис.4.8(а)					mz
						mz
		m z				a
						a

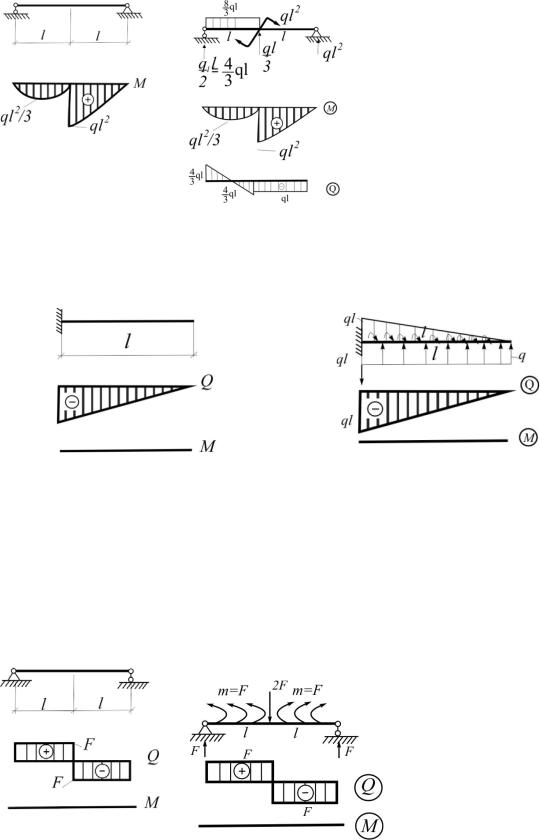
4.9. По заданной эпюре М построить эпюру Q и установить действующую на балку нагрузку (рис.4.11).

		Решение
			dM	Q
			dz
q	l2		ql2	, q	8	q.
q	8		3	, q	3	q.
1	8		3	1	3
Рис.4.11

Рис.4.11(а)

4.12. Установить действующую на балку нагрузку по эпюрам Q и

М (рис.4.12).

Рис.4.12

Решение

dM	Q m :	m z Q;

dz
dQ	q,	Q F
	q,	Q F
dz

4.13. По эпюрам Q и М подобрать нагрузку на балку. Объяснить кажущееся противоречие в эпюрах с точки зрения дифференциальных зависимостей при изгибе (рис.4.13).

Решение dMdz Q m, m z Q

Q F

Рис.4.13

Рис.4.13(а)

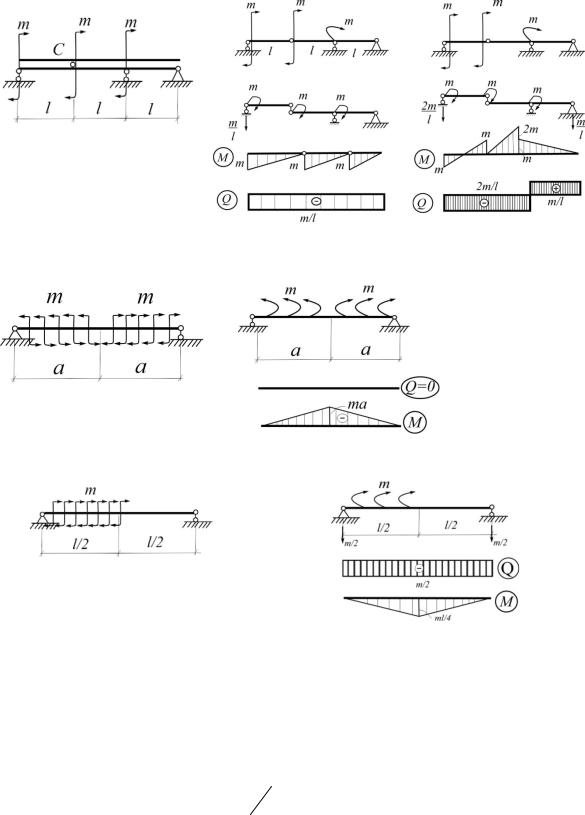
4.14. Для заданной балки (рис.4.14) построить эпюры Q и М. Как

изменятся эпюры, если момент m поместить слева от шарнира С?

Решение

Рис.4.14 Рис.4.14(а) Рис.4.14(б)

4.15.Построить эпюры Q и М (рис.4.15).

Решение dMdz Q m

Рис.4.15

Рис.4.15 (а)

4.16. Построить эпюры Q и М (рис.4.16).

Рис.4.16	Рис.4.16(а)
Решение
dM	Q m
dz

M1 z m z m2 z m2 z

0 z l 2

<<< < Предыдущая 1 2 3 4 5 67 / 177 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.06.20248.07 Mб02377.pdf
#
17.06.20248.08 Mб02378.pdf
#
17.06.20248.08 Mб02379.pdf
#
17.06.2024243.89 Кб0238.pdf
#
17.06.20248.09 Mб02380.pdf
#
17.06.20248.13 Mб62381.pdf
#
17.06.20248.16 Mб02382.pdf
#
17.06.20248.23 Mб02383.pdf
#
17.06.20248.23 Mб02384.pdf
#
17.06.20248.23 Mб42385.pdf
#
17.06.20248.24 Mб02386.pdf