Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2381

.pdf

Скачиваний:

Добавлен:

17.06.2024

Размер:

8.13 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 176 7 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

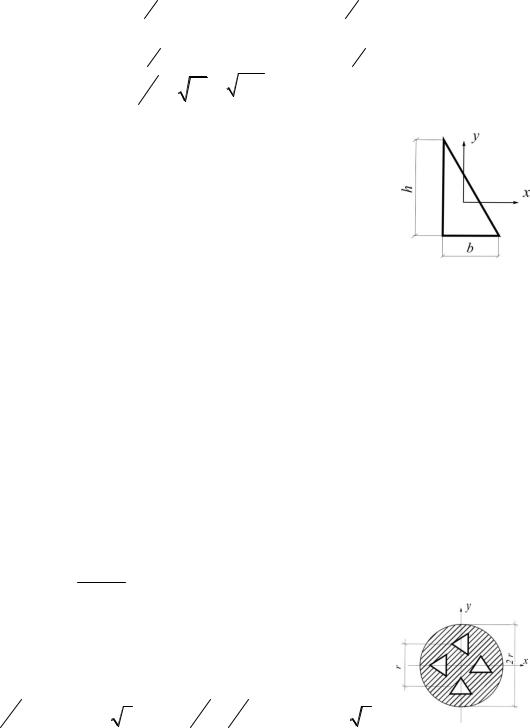
Решение

	Anetto Aбр Акап Aбр 1 0,25				0,75 Aбр.
		a			y3	a				a4	a4 .
Ix	dAnetto y2	2 dy a 0,75 y2		3a	y3		2		3
Ix	dAnetto y2	2 dy a 0,75 y2		4					4
	A	a	2	4	3	a		2	4	12	16
	бр		2					2

a 2 4 Ix 4 104 10 см.

Ответ: a 20 см.

3.15. Определить центробежный момент инерции Izу прямоугольного треугольника относительно центральных осей x, у, параллельных катетам, не прибегая к интегрированию (рис.3.17).

Решение

		h	x y	b b y										h				b b y
		h			h									h						h							Рис.3.17
Ix0 yo dAx0 yo						dx dy x y ydy															xdx						Рис.3.17
Ix0 yo dAx0 yo						dx dy x y ydy															xdx
A		0		0										0					0
	h			b	2		1		h	1		2			2	b2					b		2	y	2
		ydy b		h	y		2			2	b				2		h	y						y		ydy
				h			2			2							h				h
	0								0
				b2 y2					b2		y3			1	b			2		y2		h
				b2 y2					b2		y3			1	b			2		y2		h

					2 2				h 3					2					4
					2 2				h 3					2	h				4
																						0
																						0
		b2h2 b2h2					b2h2				b2h2					6 8 3 b2h2											;
		4			3				8				24												24
		Ixy Ix y			A		h	b			b2 h2						b2		h2					b2 h2			.
		Ixy Ix y			A		3	3			24							18							72		.
			0	0			3	3			24							18							72
			0	0

Ответ: Ixy b272h2 .

3.18. Найти осевой момент инерции Ix круга, ослабленного отверстиями в форме равносторонних треугольников со стороной, равной r/4 (рис.3.19).

Решение

r 4 sin 60

, I

r 4 r 4 sin 60 3

r4 3

Рис.3.19

24576

r 2

A r2

Ответ: Ix 0,772r4 .

3.19.Фигураобразованавписаннымидруг

вдруга квадратами (на рис.3.21 они заштрихованы). Вычислить момент инерции относи-

тельно оси x1, когда число квадратов стремится к бесконечности (рис.3.21).

Рис.3.21 Решение

Ix Ix			a4		a 2					4		1				a 2								2	4		1				a 2									2					2	4	1

			12				2					12							2					2			12								2					2					2		12
1			12				2					12							2					2			12								2					2					2		12
1
	a	4						1			4				1		4		1			4							2				4							1					4
	a				4			1							1				1										2								4			1
				1																															1
	12								2						2				2										2														2

									a4						1								1				a4			3				16					a	4
										1								1																								.
										1								1					1				12			4				15				15				.
									12						4				1				1				12			4				15				15
			a4																					16
Ответ:			a4	.
Ответ:			15	.
			15															3.20. Найти момент инерции Ix треуголь-
																		3.20. Найти момент инерции Ix треуголь-
														ника ОВС, если известна его площадь А и
														длины отрезков b и с (рис.3.22).
																												Решение
	Рис.3.22															A 12 Lb lb L l c 12 b c L l ,
																												L l									2A				.
																												L l													.
																L b3					l b3							L l c3								b c
													Ix			L b3												L l c3											L l					b3		c3 .
													Ix																12															b3		c3 .
						A											12							12					12									12
Ответ:			Ix			A		b2		bc c2 .
Ответ:			Ix					b2		bc c2 .
					6
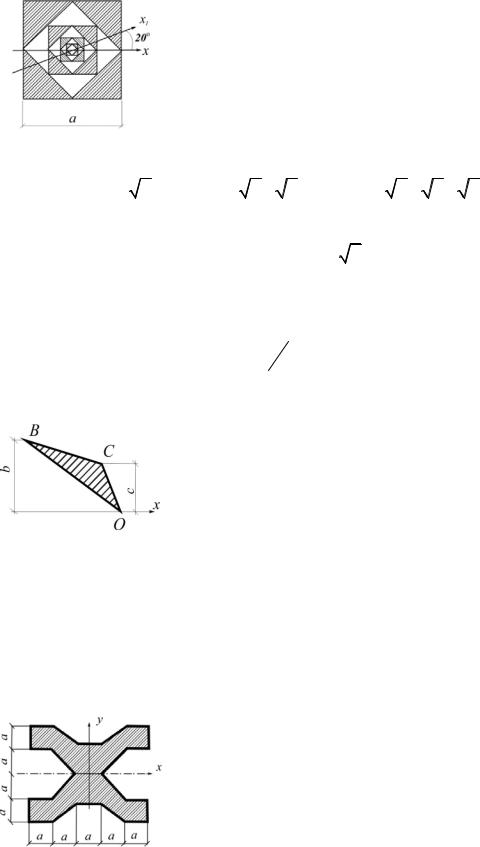
																3.21.Для заданной фигуры определить
													момент инерции относительно оси у.
																				2a 5a 3								Решение
																I y				2a 5a 3								125 a4 .
																I y								12				125 a4 .
																								12		125 a4						6
	Рис. 3.23															Ответ: I y										125 a4						.
	Рис. 3.23															Ответ: I y											6					.
																											6

3.22.При каких соотношениях h/b будут наибольшими геометрические характеристики (Ix, Wx, Ip) прямоугольника, вписанного в круг заданного радиуса r.

Решение

																										0 b							2r
b2 h2		2r				2	,			b2 1 2										2r		2	,											h				.
b2 h2		2r					,			b2 1 2										2r			,											h		0		.												Рис. 3.25
																																		b		0														Рис. 3.25
																																		b
		bh		3	b					4 3				2r	4							3
I														2r
I	x																									2
			12					12						12									2
			12					12						12					1				2
																			1
																											4			3 2		1 2					2		3 2 1 2													2
																											4			3 2		1 2					2		3 2 1 2													2
Ix		Imax , если											Ix' 0 : 2r																																									0
Ix		Imax , если											Ix' 0 : 2r																																4									0
																							12																			2
																							12														1					2
																																					1
						3 2 1 2 2 4 4 1 2 ,																										2 3,									3.
					2					3	2		2r				2				2				2r								2r			3									2
W bh									b																2r								2r
W bh																		1 2																6
		x	6							6				6				1 2									1 2							6												2			3	2

																																								1
																												3 2 1							2		32						2 3						1		2		12	2
																												3 2 1																		2			1					2
W W								,		если W ' 0 : 2r																																				2									0
W W								,		если W ' 0 : 2r																																													0
		x			max									x										6																						2
		x			max									x										6																1						2		3
																																								1
												2 1 2								3 2 0, 2 2, 2.
													3	3		h					4		3										2r		4					3									2r				4
I Ix Iy										bh				b		h		b															2r
I Ix Iy										bh				b				b																													2							2
										12				12						12													12											2						12				1
										12				12						12													12					1						2						12				1
																																						1
																								2r 4							1 1 2												2
I Imax ,										если				I '					0 :					2r 4							1 1 2												2							0
I Imax ,										если				I '					0 :																															0
																										12													2		2
																										12								1					2		2
																																		1

																				2 1,									1.
Ответ: ξ							3,			ξ				2 , ξ 1.

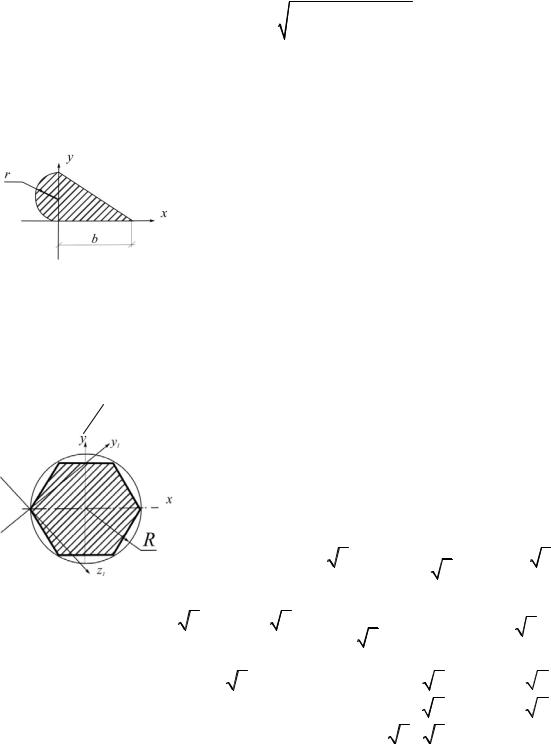
3.23.Доказать, что для любой плоской фигуры справедливо неравенство: Ix Iу > Ixу, где x, у – две произвольныевзаимно перпендикуляр-

ные оси (рис.3.26).

Рис.3.26

	Решение
Imin	Ix Iy	1	Ix Iy 2	4Ixy2	0
	2	2

Ix I y 2 Ix I y 2 4Ixy2

2Iy 2Ix 4Ixy2 .

Ответ: Ix I y Ix2y .

3.24. Сечение составлено из полукруга радиуса r и прямоугольного треугольника с основанием b. При каком соотношении b/r центробежный момент Ixy равен нулю

		(рис.3.27)?									Решение
Рис.3.27											Решение
			r	2		4		r			b2 2r 2
		Ixy							r			0
		Ixy	2			3			r	24		0
			2			3				24
		2 r4		b2r2			,			4r2 b2.
Ответ: b		3			6
Ответ: b	r	2.
	r

3.25. В окружность радиуса R вписан правильный шестиугольник. Определить центробежный момент шестиугольника относительно осей x1, у1 (рис.3.28).

Решение

					A		2R R		R		3	2 R21,5				3 R2					24	3 .
					A							2 R21,5				3 R2					24	3 .
Рис.3.28			R 3 3				2			2											16
Ix I y 2	R		R 3 3			R	R 3 3			R	4			1	1				R	4	5 3
													3									.
	2		48				12						3	16							16	.
	2		48				12							16	4						16
I y I y A R2		R4			29	3	; Ixy	0;					sin			3	, cos					4	.
I y I y A R2		R4			16		; Ixy	0;					sin			7	, cos					7	.
0					16		0									7						7
0							0
I y1x1		I yo		Ix sin cos R								4	24	3		3 2		.
I y1x1		I yo		Ix sin cos R								4	16			7		.
													16			7

Ответ: 79 R4.

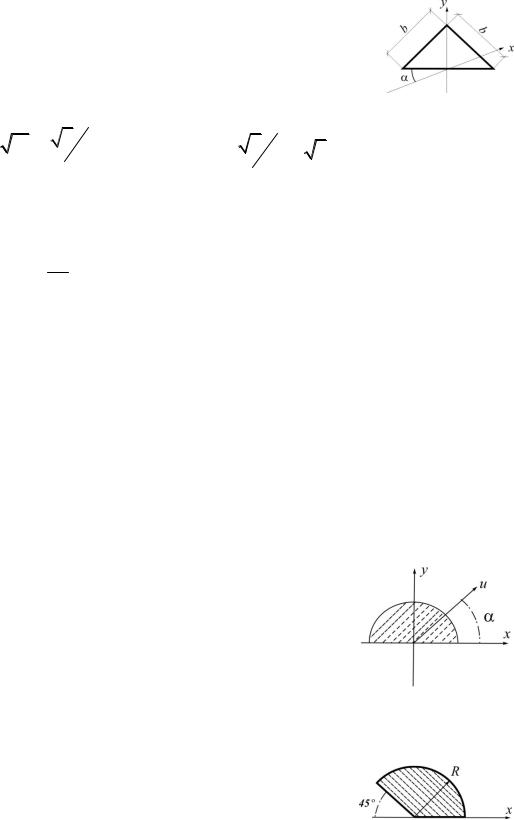
3.26.Определить осевой момент инерции равнобедренного прямоугольного треугольника относительно оси x. Размер b и угол α заданы

(рис.3.29).

Решение

	b			3		4
	b	2 b 2	2		b	4
Ix			2		b		,
Ix		12			24		,
0		12			24
0

Ix0

Ответ: Ix b4 .

I y0

Iy0

b 2	2 b 2 3	b4
		24 ,
	48

Ix b4 .

Рис.3.29

Ix0 y0 0 :

3.27. Известны моменты инерции Ix, Iу, Ixу. Составить формулу для определенияуглаα, накоторыйнужноповернутьосиx, у, чтобыосевые моменты инерции относительно новых осей х1 и у1 были одинаковыми.

Решение

Ix	Iy			: Ix cos2			I y sin2 Ixy sin 2 Ix sin2 I y cos2 Ixy sin 2 ,
1			1					Ix cos 2 Iy cos 2 2Ixy sin 2 0.
								Ix cos 2 Iy cos 2 2Ixy sin 2 0.
																	Ix Iy		tg2 .
																	2Ixy		tg2 .
																	2Ixy
											Ix	I y
Ответ: α 1 arctg											Ix	I y			.
Ответ: α 1 arctg															.
					2						2Ixy
					2						2Ixy
	3.28.Показать, что момент инерции фигуры
относительно						оси и						не			зависит					от		угла	α
(рис.3.31).								Решение
								Решение												r	4
				Ixy 0,					Iu Ix Iy									1		r	4
				Ixy 0,					Iu Ix Iy									2		4	.		Рис.3.31
						πr	4											2		4

	Ответ: Iu							.
	Ответ: Iu					8		.
						8
	3.32. Определить момент инерции плоской
фигуры относительно оси x (рис.3.32).
								Решение															Рис.3.32
		1		R4		1			R4				R4					1			R4	3	2
Ix					Ix
Ix		2		4	Ix					8				8				2			32
		2		4						8				8		4		2			32


	4		R4		R4	sin 2		R4		1
1		2					4
Ix	sin			d
			4		4	2		8	4	2
	0						0

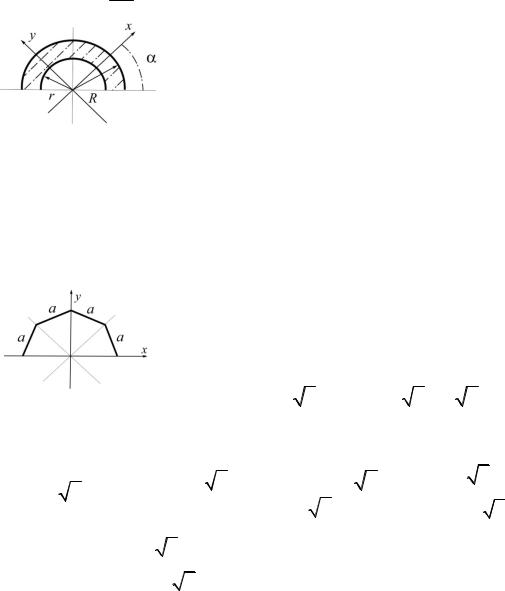
Ответ: Ix R324

Рис.3.33

3π 2 .

3.33. Для плоской фигуры найти осевые

моменты инерции Ix и Iу . Известны R, r, α.

Решение

	Ix	I y	1		R	4	4	; Ix y		0
	Ix	I y	1		R	r		; Ix y	0	0
	0	0	2		4	4		0	0
						R4 r4
Ix Iy Ix				I y		R4 r4
			0		0	8
						8

Ответ: Ix I y

Рис.3.34

π8 R4 r4 .

3.34. Определить Ix для заданной плоской фигуры – половины правильного восьмиугольника (рис.3.34).

Решение

	R	2 1 R	3	R 2 R 2 / 2	3
Ix 2	R	2 1 R		R 2 R 2 / 2

		12		12
		12		12

	R4			1		4		2 2 1		a4	2 2 1	a4	2 2 1
		2 1			R									.
6		2 1		2	R				2	6 4 2	2	4 3 2 2		.
6				2					2	6 4 2	2	4 3 2 2
Ответ:		Ix	a4 2 2 1						.
Ответ:		Ix	4 3 2				2		.

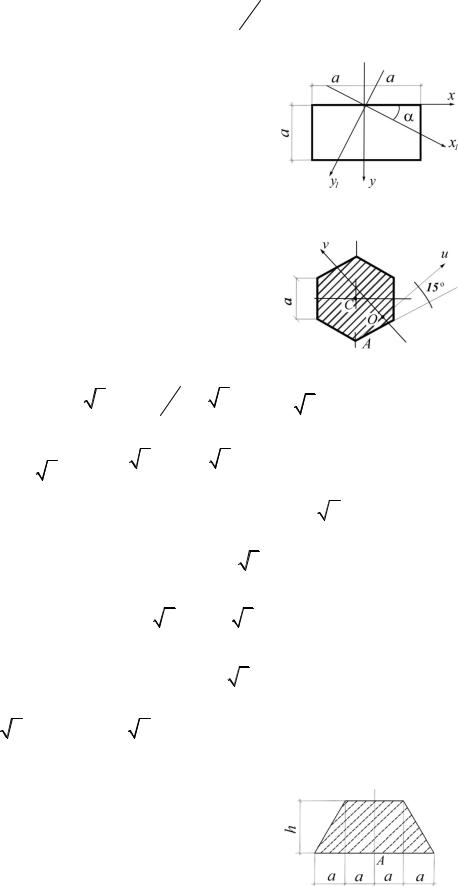
3.35. Определить, при каком значении п оси x и y будут главными

(рис.3.35).

				Решение
	2R R				R	R2			4 R
Ixy 2			R				R
Ixy 2	2		R		3	2	R
	2				3	2			3
		nR 2		R		4 nR
						3		0,
			2					0,
			2

1		2		2 n3	0,	n3 1	2	.
3		3		3			2

Ответ: n 0,794.

3.36. Показать, что при любом α оси x1 и у1 являются главными (рис.3.36).

Решение

2a a

2 a

4 , Iy

a 2a

2 a4

, Ixy 0;

Рис.3.36

3.37. Задан правильный шестиугольник со стороной а. Найти на оси и положение точки О, для которой оси v и u будут главными осями инерции и полярный момент инерции фигуры относительно этой точки (рис.3.37).

								Решение																					Рис.3.37
								a a 3 3							a 2 a					3 3				4			3 5
Ix		Iy											2								a								,
Ix		Iy						12					2						48		a					16			,
	c				c			12											48							16
	c				c
A a a							3 2		a			a		3			a2		3	3
A a a							3 2		2					2					2
									2					2					2
I	x y			0,			V U через ц.т. фигуры,																v			a		2		.
I				0,			V U через ц.т. фигуры,																v			a				.
																								o		2
	c		c																							2
	c		c
								Iv Iu				Ix				I y			a4 5 3				;
										c				c				c			16
										c				c				c
															2			2		17	3			4
						Iu Iu					A			a								a			;
						Iu Iu					A			a	2					16		a			;
								c							2					16
								c
								I Iu Iv								a4 22					3 .
																				16
Ответ: vo a				2	,		Iρ a4				11			3		.
Ответ: vo a				2	,		Iρ a4									.
				2								8

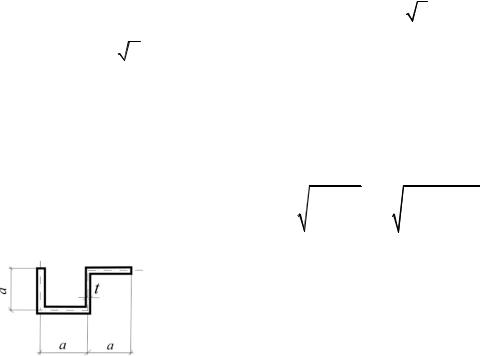
3.38. При каком значении h любая ось, проходящая через точку А сечения, будет главной? Размер а задан (рис.3.38).

Рис.3.38

Решение

			2a h				3		2 ah		3	a h3		5
Ix	A		2a h						2 ah			a h3		5	;
	A				3					12				6
				h 2a 3						ha3			ha	4		2	3		45
I y										2					a		a	h		.
I y		A			12					2			2	3	a		a	h	18	.
		A			12					36			2	3					18

			I	xA	I	yA		:		h2 5 a2 45				, h a 3.
				xA		yA				6			18
										6			18

Ответ: h a 3.

3.39. Фигура имеет площадь А = 10 см2, главные центральные моменты инерции Iv = 410 см4, Iи = 320 см4. На главнойосиv найти такие точки, чтобы все оси, проходящие через них, были главными для данной фигуры.

Решение

A V

2 ,

Iv Iu

410 320

3 см.

Ответ: V 3 см.

3.41. Определить величины главных мо-

ментов инерции относительно главных цент-

ральных осей заданной тонкостенной фигуры.

Толщинастенкиt постояннаималапосравнению

Рис.3.41

с а. Размеры даны по средней линии сечения

(рис.3.41).

Решение

0 0,5a a 1,5a

0,75 a

4a t

A=4a t,

a .

2 at a / 2 2 2 a3 t 2

at 0,75a

a3 t

at 0,25a

I y

at 0,25a

a3t

at 0,75a

at 0,5a 0,25a at 0,5a

0,75a a t

	Ix	I y			1													25 15	3	5
Imax	Ix	I y			1		Ix	Iy			2					I 2 x y	a3t	25 15	a t			3 .
	c		c										4							5
		2			2					c			4					24
							c			c						c c			a3t
min																			a3t		12
			5							5											12
Ответ:	Imax		5	a	3	t ;	Imin			5		a		3	t .
Ответ:	Imax		3	a		t ;	Imin		12			a			t .
			3						12

3.42.Для прямоугольника со сторонами b = 2 см и h = 3 см определить положение главных осей, проходящих через О, и вычислить главные моменты инерции (рис.3.42).

Решение

Рис.3.42

2Ixy

3 18 см

;

tg2

1,8

Ix I y

8 см4;

Iy bh

23,3 см

b h

b2h2

9 см

Imax 13 10,3

2,7 см

min

2 2

Ответ: α

arctg 1,8

, т.е. .Imax 23,3см4;

Imin 2,7 см4.

3.43. Фигура представляет собой полукруг, ослабленный прямоугольным вырезом со сторонами b иh. Прикаком отношении h/b момент инерции относительно оси z не будет зависеть от угла α (рис.3.43).

Решение

Рис.3.43

Ixy 0;

b3h

;

I y

bh3

Iz Ix I y :

b2 h2 .

Ответ:

3.44. Вычислить осевой момент инерции изображенной фигуры относительно главной центральной оси u (рис.3.44).

Рис.3.44

Ответ: Iu 25312 a4.

Рис.3.45

Решение

	4a	4	a	4	253		4
		3				a
Iu	12		12		12

3.45. В системе осей x, у определить точки, каждая из которых обладает тем свойством, что две любые взаимно перпендикулярные оси, пересекающиеся в этой точке, являются главными осями инерции заданной фигуры (рис.3.45).

Решение

b2 /12

h b : bh

hb x02 ,

bh3

hb3

/ 12

b h :

bh Y0

при h

b :

h2 b2 /12

Ответ:

b :

/ 12

при h

3.46. Для плоской фигуры найти точку, обладающую свойством, что все проходящие через нее оси являются главными. Считать известными: положение центра тяжести, A, Ix, Iу, Ixу, x, у – заданные

центральные оси координат.

			Решение
tg2 0	2Ixy	,	Imax	Ix Iy	1	Ix Iy 2 4Ixy2
				2	2
	Ix Iy		min

A z2 Imin Imax ,

Ответ: I I : x zcosα0 ; x y y zsinα0

			Ix Iy			2	4Ixy2
			Ix Iy				4Ixy2
z
z				A
				A

		1				2Ixy
			arctg
		2	arctg		Ix I y
	0	2			Ix I y

I I : x zsinα0 . x y y zcosα0

<<< < Предыдущая 1 2 3 4 56 / 176 7 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.06.20248.07 Mб02377.pdf
#
17.06.20248.08 Mб02378.pdf
#
17.06.20248.08 Mб02379.pdf
#
17.06.2024243.89 Кб0238.pdf
#
17.06.20248.09 Mб02380.pdf
#
17.06.20248.13 Mб62381.pdf
#
17.06.20248.16 Mб02382.pdf
#
17.06.20248.23 Mб02383.pdf
#
17.06.20248.23 Mб02384.pdf
#
17.06.20248.23 Mб42385.pdf
#
17.06.20248.24 Mб02386.pdf