Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2381

.pdf

Скачиваний:

Добавлен:

17.06.2024

Размер:

8.13 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 175 6 7 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

2.33. Определить изменение прямого угла DBC, выделенного в окрестности точки В, если сосредоточенную силу F повернуть в плоскости чертежа на угол π/2. Модуль сдвига G и площадь прямоугольного поперечного сечения стержня А считать известными. Точка В лежит на продольной оси стержня (рис.2.33).

Решение

yB 0;

45 : z

sin 2

cos 2 z

1 .

а)

Растяжение:

F : z

(уменьшение);

2GA

z M x

б) Изгиб: M x F z,

Qy F :

yB 0 :

2 G1 0 нет изменения ;

в) 2 1 F .

2GA

Ответ: угол увеличится на F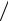 2GA .

2.34. Определить, при каком соотношении между напряжениями σх, σу, τy в данной точке материала возникает линейное напряженное состояние (рис.2.34).

Решение

1 max	x y	1	x y 2 4 2	0;
	2	2

Рис. 2.33

0 :

Рис. 2.34

2	min	x y	1	x y 2 4 2
		2	2

x y 2 x y 2 4 2 , 2 x y 2 x y

Ответ: σxσy τ2.

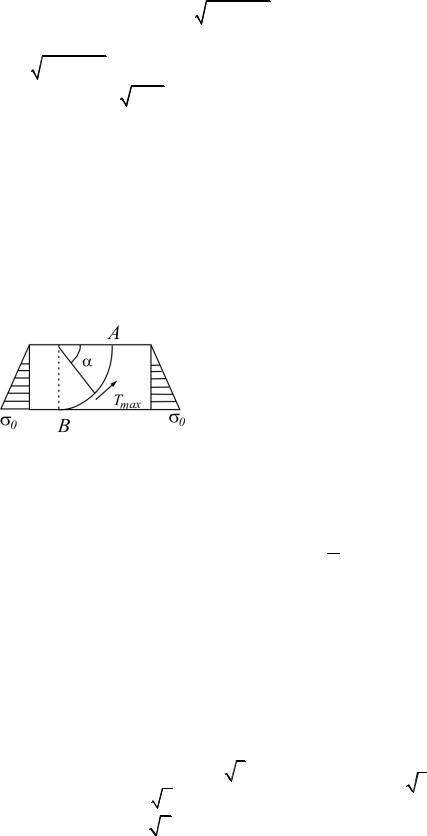
2.35. К элементу приложено напряжение σ. Какое касательное напряжение τ нужно дополнительно приложить, чтобы τmax в материале увеличилось в два раза (рис.2.35)?

Решение

а) 'max 2 ;

4 2

Рис. 2.35

б) ''max	max min	2 4 2	;
		2
	2

в) 2 4 2 2 .

Ответ: τ σ 3 / 4.

2.37. В растянутом вдоль оси стержне нормальные напряжения по одному из наклонных сечений равны 75 МПа, а касательные – 43,3 МПа. Определить σmax в стержне и угол наклона площадки к поперечному сечению.

Решение

	z cos		2	75 МПа
	z cos			75 МПа
		sin 2		,
z		sin 2	43,3 МПа
		2

Ответ: 100 МПа, 30 .


tg		0,5773 ,	30 ;
tg		0,5773 ,	30 ;

	z 100 МПа.
	z 100 МПа.

	2.39. Полоса, склеенная по дуге окруж-
	ности AB из двух однородных материалов,
	находится	в	линейном напряженном
	состоянии. Во всех поперечных сечениях
	напряжения распределяются по указан-
Рис. 2.39	ному на рисунке закону. Определить τmax
	в склейке	и	угол α, соответствующий

точке, в которой действует τmax

Решение

y h sin : z 0 hy 0 sin .

				2	0			sin cos			2
z cos					0			sin cos				; '				2sin cos				2		sin3		.
	z sin 2 0											; '				2sin cos				2		sin3		.
	z sin 2 0							sin2		α cos				0							0
			2							0 : sin 2cos2 sin2 0,
		max , если '								0 : sin 2cos2 sin2 0,
																			2	1/ 3
	2cos2 sin2 0,									3cos2		1 0			,		cos			1/ 3			.
	2cos2 sin2 0,									3cos2		1 0			,					2 / 3			.
																	sin2			2 / 3

	max	0			2	1	0		2	3 ,			arctg					3 / 3 54,7 .
	max	0			2	3	0			3 ,			arctg					3 / 3 54,7 .
					3	3				9
Ответ:					2	3	, α 54,7 .
Ответ:		max			0	9	, α 54,7 .
		max			0	9

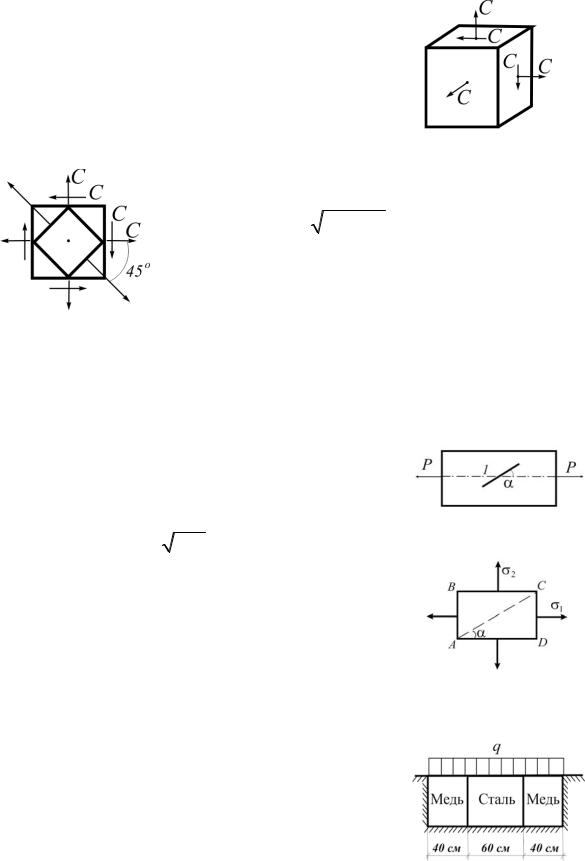
2.40. Какое напряженное состояние (линейное, плоское или объемное) возникает в данной точке материала? Определить величину главных напряжений и положение главных площадок (рис.2.40).

Решение

								Рис. 2.40
2 C
		2c	1					2C 1
	max	2c	1	0	2	4c	2	2C 1		;
	max	2	2	0		4c		C C	0 3	;
	min	2	2						0 3

1 2С, 2 С, 3 0 :

Плоское напряженное состояние. Ответ: σ1 2С, σ2 С, σ3 0; α 45 .

Задачи для самостоятельного решения

1. На стержень установлен тензометр под углом α к продольной оси. При каком α имеет место равенство 1 = 2, где 1 и 2, – отсчеты по тензометру до и после действия силы F.

Ответ: α arctg 1 / ν.

2. При каком соотношении между напряжениями σ1 и σ2 длина диагонали AC элемента ABCD не изменится, если коэффициент Пуассона материала равен v ?

Ответ:	σ1		ν tg2α	.
	σ2		1 νtg2α

3. Три пластины единичной толщины были плотно вставлены в недеформируемую обойму. Затемкнимбылаприложенанагрузка q, как показано на рисунке. Определить главные напряжения в пластинках. Трением между пластинками пренебречь: Ест/Ем =2.

Ответ: σ1 0 , σ2 νq, σ3 q.

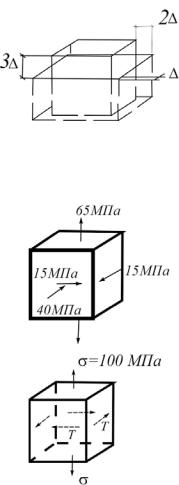
4. Кубик из изотропного упругого материала вставлен в гнездо абсолютно жесткой плиты (рис.2.28). Под действием давления, приложенного к выступающей грани зазоры закрываются, и в момент закрытия последнего зазора верхняя грань достигает уровня поверхности плиты. Найти коэффициент Пуассона материала кубика.

Ответ: ν 0,5.

5. Определить наибольшее касательное напряжение (рис.2.38).

Ответ: τmax 55 МПа.

6. Какое наибольшее значение касательных напряжений τ можно допустить, чтобы

τmax в материале не превзошло 80 МПа?

Ответ: 60 МПа.

Рис. 2.36

Глава3. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ ФИГУР

Краткие теоретические сведения Основные понятия и обозначения

Sx	ydA статический момент фигуры относительно осиx y : x y ;
	A
Ix	y2dA осевой момент инерции			относительно осиx y : x y ;
	A
W		Ix	осевой момент сопротивления относительно осиx y : x y ;
W			осевой момент сопротивления относительно осиx y : x y ;
x		ymax
		ymax

Ixy xydA центробежный момент инерции относительно осейx, y;

I 2dA полярный момент инерции относительно полюса;

I Ix Iy если полюс совпадает с началом декартовых координатx, y;

центральная ось, проходящая через центр тяжести фигуры Sx 0;

главные оси, относительно которых Ixy 0;

ось симметрии фигуры главная центральная ось.

A Yc ,

Параллельный перенос осей:

где Yc расстояние от центра тяжести фигуры до осиx1;

A Y 2

, гдеY

расстояние от центральной

оси x до любой оси x ;

следствие: относительно центральных осей осевые моменты инерции

фигуры принимают минимальное значение.

Тензор моментов инерции: TI

Ixy

I y

Iuv

Поворот осей x,u 0,если :

Ix cos2 I y sin2 Ixy sin 2 ,

Ix sin2 I y cos2 Ixy sin 2 ;

Iuv Ixy cos 2 (Ix Iy )

sin 2

;

следствия:

1) относительно главных осей осевые моменты инерции фигуры

принимают экстремальные значения;

2) если относительно главных осей xy Ixy 0

осевые моменты инерции

равны Ix Iy , то оси uv главные Iuv 0 и

Ix Iy Iu Iv ;

3) инварианты тензора: Iu Iv Ix I y ,

Iu Iv Iuv2

Ix I y

Ixy2 ;

главные моменты инерции: I1,2

Ix Iy

Ix Iy 2

4Ixy2 ;

Ixy

главные оси: tan 1,2

1,2 x, 1,2

0, если ;

Iy I1,2

центробежный момент инерции: max

Iuv

Ix Iy 2

4Ixy2 .

Для правильных фигур (более двух осей симметрии) все центральные

оси являются главными

центральными

осями

( Ixy Iuv 0 ) и

Ix Iy Iu Iv.

Примеры решения задач

3.1. Определитьположениецентра тяжестизаданнойфигурыпутем построения с помощью одной линейки (рис.3.1).

Решение

Рис. 3.1

Рис. 3.1(а)

3.2. Показать положение главных центральных осей заданной фигуры (не прибегая к вычислениям) (рис.3.2).

Решение

Рис. 3.2	Рис. 3.2 (a)

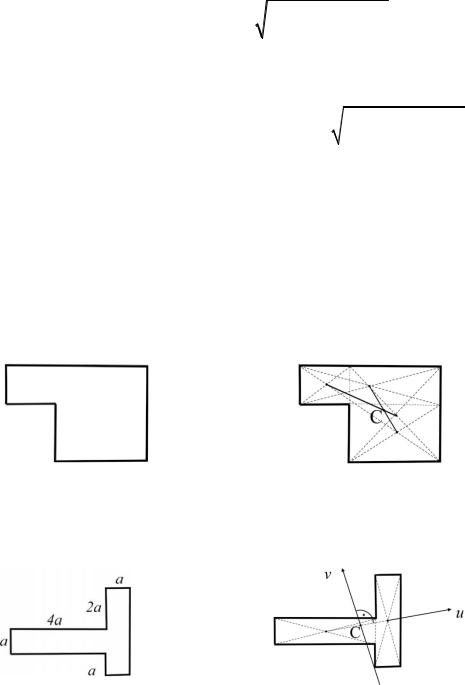
3.3. Показать положение главных центральных осей заданной фигуры (не прибегая к вычислениям) (рис.3.3).

Решение

Рис. 3.3

3.4. Из равнобедренного треугольника ABC вырезан равнобедренный треугольник ADC. Опреде-лить высоту вырезанного треугольника, если вершина его D является

центром тяжести оставшейся фигуры (на Рис.3.4 рисунке заштрихована) (рис.3.4).

a h

H 2

H h

2 3

h ,

aH ah

H h

Ответ: h H2 .

3.5.Вычислить момент инерции фигуры относительно оси x (рис.3.5).

Решение

		h		y3	4	bh3 .
					4

Ix y2dA bdy y2			b
Ix y2dA bdy y2			b
A	0		3		0	3
A	0		3		0
Ответ:	bh3					Рис.3.5
		.
	3	.

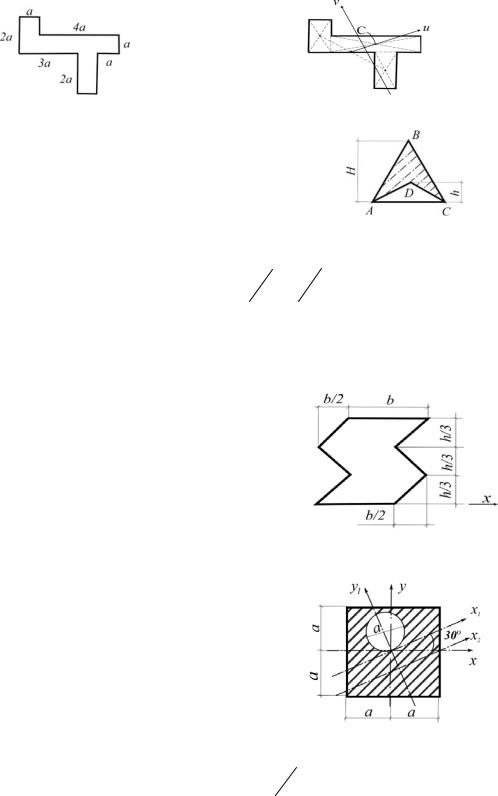
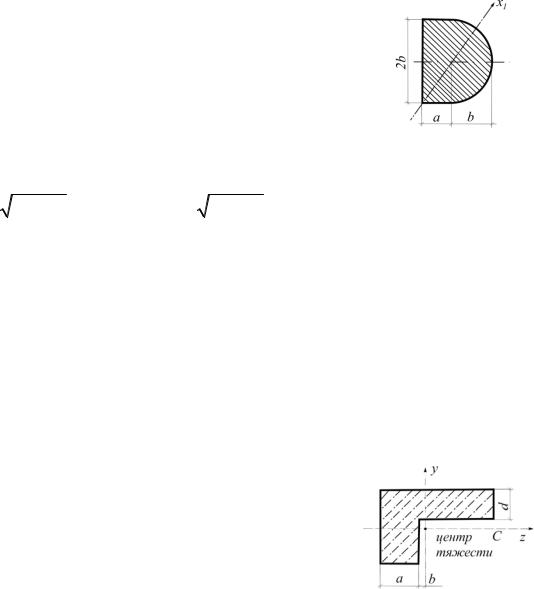
3.6. Определить момент инерции заштрихованной фигуры относительно центральной оси x2 параллельной x1 (рис.3.6).

Решение

	2a	4				4		2	a		2	4
Ix				a			a		a		1,088 a	4	;
Ix	12			64			4				1,088 a		;
1	12			64			4		2

			Y		Sx1				2a 2 0 a2 / 4 a 2
			Y		Sx1
			1c			A				2a 2 a2 / 4

Ix2 Ix1 2a)2 a2 / 4 Y12c 1,04 a4.

Рис.3.6

0,1222 a;

Ответ: 1,04 a4.

	3.7. Вычислить				полярный				момент
	инерции треугольника относительно на-
	чала координат. Треугольник задан коор-
	динатами своих вершин (в см) (рис.3.7).
			Решение
		9 63	54 8	2	9 33	27	6	2
	Ix	12	54 8		36	2	6
Рис.3.7		12			36	2

						3 33					9		10			2				64					36					9		2				1179 см											4	;
							36				2		10							36						2				9						1179 см												;
							36				2									36						2
					Iy				6 93											2						3 93										27			10				2
					Iy			12							54 8,5													36								2			10
								12																				36								2
							34			9					2				64					36							2														4
												12																	6						1521 см											.
							36			2		12							36						2				6						1521 см											.
							36			2									36						2
Ответ: Iρ Ix						I y 2700 см4 .
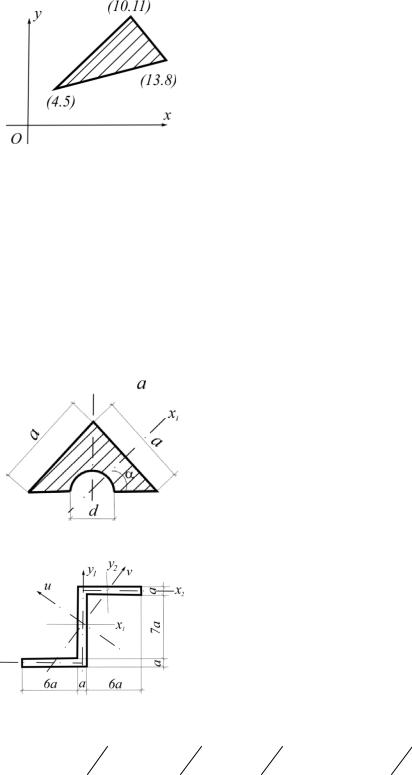
																		3.8.Определить момент инерции фигу-
														ры относительно оси x1 (рис.3.8).
																																	Решение
																											Ix							1			a		4				1 d 4
																											Ix							2			12						2		64					.
																												1						2			12						2		64
																												1
														Ответ:							Ix			0,					5						4				πd			4
	Рис.3.8													Ответ:							Ix			0,					5		a								πd				.
	Рис.3.8																					1											12							64
																						1
																		3.9. Вычислить центробежный момент
														инерции										плоской														фигуры												относительно
														осей u, v, при этом ось v проходит через
														центры											тяжестей																	трех								одинаковых
														прямоугольников,																								составляющих фигуру
														(рис.3.9).
	Рис.3.9															Решение
																Решение
sin 4			5		,	cos 3						5		,	tg 4						3	,						sin 2 24													25			, cos 2 7 .
			5									5									3																				25										25
		7a				a	3				I			7a					3	a ,								I							0
I	x1	7a				a	,				I	y1		7a						a ,								I		x1y1					0
	x1				12							y1						12												x1y1
				Ix		I y											7a a						1		a2																24								336
	1			Ix		I y											7a a						1															2			24								336
Iuv					1		1		sin 2																									7a																	a4
Iuv						2			sin 2									12					2											7a							25									25	a4
						2												12					2																		25									25

		(7a)		3	a ,	I y		7a a	3	,	Ix y		0
Ix		(7a)			a ,	I y	2	7a a		,	Ix y		0
	2	12					2	12			1	1
			Ix2 I y2			sin 2 7a a 1					7a 2		a2 24	336 a4
Iuv2			Ix2 I y2
Iuv2
		2						12		2			25	25
		2						12		2			25	25
					Iuv 2Iuv1		Iuv2			336 a4 13, 44a4.
										25

Ответ: Iuv 13,44a4.

3.10.Определить момент инерции фигуры относительно оси x1.

Решение

				1	b4	1
				Ix	4	2
				1	4	2
				1
										Рис. 3.10
sin		b		,	cos		a
sin		a2 b2		,	cos		a2 b2
2	a 2b 3				2	a 3 2b			2
Ix			,		Iy			, Ixy		0,
Ix		12	,		Iy		3	, Ixy		0,
		12					3

Ix2 Ix2 cos2

I y2 sin2

a 2b 3

a 3 2b

a2 b2

4a3b3

Ix1 Ix1

Ix1

3 a2 b2

Ответ: Ix1

π b4

4a3b3

3 a2 b2

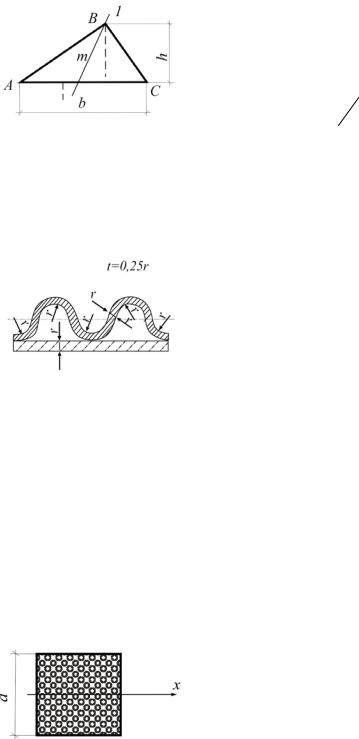
3.11. Вывести формулу центробежного момента инерции относительно осей х, у, проходящих через центр тяжести заштрихованной фигуры (рис.3.11).

Решение

Sx 0 :

Sy 0 :

A1 y1	d
A1 y1	A2	2	c
		2		;
A2 x2	a
A2 x2	A1	2	b
		2

	b2		4		a3b3
	a2 b2		3		a2 b2

Рис.3.11

I	xy	A	y	a		b	A x	d		c
	xy	1	1		2		2 2		2
					2				2

A A

1 2

Ответ:

3.12.Найти момент инерции треугольника ABC относительно оси 1-1, совпадающей с медианойРазмеры b, h, m заданы (рис.3.12).

Решение

sin h

b sin b

Рис.3.12

2 m

1 1

48 m2

Ответ: I1 1

48 m2

3.13.Для составного профиля, изобра-

женного на рисунке, определить момент

инерции

относительно

горизонтальной

центральной оси (рис.3.13).

Рис.3.13

Решение

4 2r t t r 1,5t 0

2, 25r2 1,375r 0

2, 25r2 1,125r2 0,53485r.

4 2r t t r t 2

r t

r4 / 4

1,125 r2

0,53485r 2

9r t3

0,84015r

3, 275r

1,600r

2, 25r

Ответ: 4,875 r4.

3.14.Стержень

квадратного сечения

выполнен из материала с капиллярами,

ориентированными вдоль оси стержня и

равномерно распределенными по площади

сечения

коэффициентом

пористости

Рис.3.16

Акап/Абр=0,25. Определить размер сечения,

для которого Ix = 10000 см4 (рис.3.16).

<<< < Предыдущая 1 2 3 45 / 175 6 7 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.06.20248.07 Mб02377.pdf
#
17.06.20248.08 Mб02378.pdf
#
17.06.20248.08 Mб02379.pdf
#
17.06.2024243.89 Кб0238.pdf
#
17.06.20248.09 Mб02380.pdf
#
17.06.20248.13 Mб62381.pdf
#
17.06.20248.16 Mб02382.pdf
#
17.06.20248.23 Mб02383.pdf
#
17.06.20248.23 Mб02384.pdf
#
17.06.20248.23 Mб42385.pdf
#
17.06.20248.24 Mб02386.pdf