Файловый архив студентов. Файловый архив студентов.
1305 вузов, 5175 предметов.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Пензенский Государственный Университет Архитектуры и Строительства
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

2381

.pdf
Скачиваний:
6
Добавлен:
17.06.2024
Размер:
8.13 Mб
Скачать
☆

 

 

 

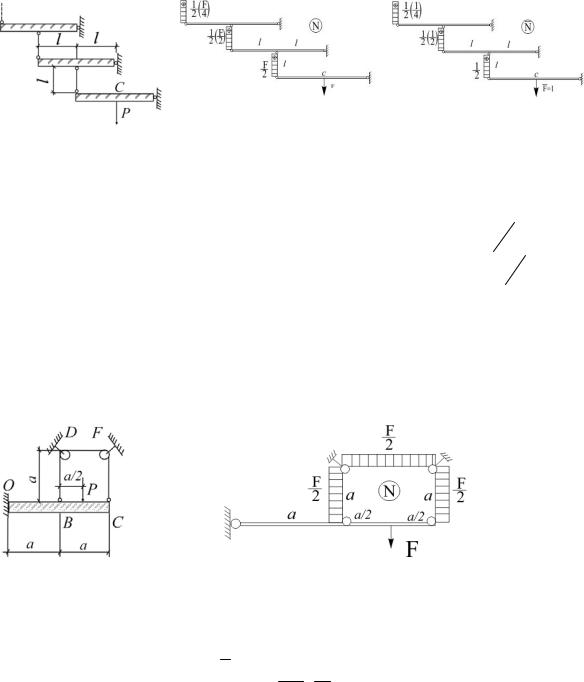
z

 

1

 

z

 

C 0 :

1

 

 

 

 

 

 

 

0.

 

2

l

 

 

 

l

 

 

 

Ответ: z 23 l.

1.31. Стержневая система состоит из бесконечного числа абсолютно жестких горизонтальных стержней и подвесок одинаковой длины l и жесткости ЕА. Определить перемещение точки С (рис.1.31).

Рис. 1.31

Рис. 1.31(а)

Рис. 1.31(б)

 

Решение

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

F

 

1

 

1

 

F

 

 

 

 

1

 

1

 

1

 

F

 

 

 

1

 

1

 

 

 

 

 

 

 

 

 

 

 

 

NN

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

с

 

 

EA

 

 

ds

 

 

 

 

 

 

 

l

 

 

 

 

 

 

 

 

 

l

 

 

 

 

 

 

 

 

 

 

 

l

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

EA

 

 

2

 

2 2

 

2

 

 

 

2 2 2 4

 

 

 

2 4

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Fl

 

1

 

 

1

1

 

 

1

 

 

1

 

 

 

 

 

 

Fl

 

 

 

a qi

 

 

Fl

 

 

a

 

 

 

 

Fl

 

 

 

1

4

 

 

 

Fl

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

EA

 

4

 

 

4

 

 

 

4 16

 

 

 

 

 

EA

 

1

 

 

 

 

EA 1 q

 

 

 

EA 1 1

 

 

 

3EA

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

i 1

 

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Fl

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Ответ:

 

с

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3EA

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1.33. Абсолютно жесткий стержень ОС поддерживается тросом BDFC, проходящим через блоки D и F. Определить – перемещение

точки приложения силы F. Найти сечение троса, остающееся неподвижным. Заданы величины F, а, А и Е троса (рис.1.33).

Рис. 1.33

Рис. 1.33(а)

 

 

 

 

Решение

 

F

 

Из равновесия: M 0 :

F 1,5a N a N 2a,

N

;

2

О

 

 

 

NNEA ds EA1 F2 12 3a 34 EAFa .

Ответ: δ

3

 

Fa

; точка D:

B

 

C

.

4

EA

lBD

lCD

 

 

 

 

 

21

Задачи для самостоятельного решения

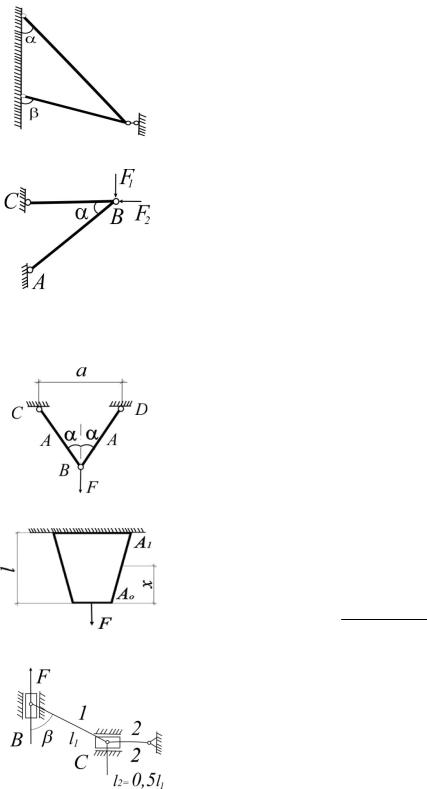
1. При каком соотношении между углами α и β в стержневой конструкции не возникают температурные напряжения? Материал и изменение температуры двух стержней одинаковы.

Ответ: / 2.

2. На

узел В

кронштейна

действуют силы

F1 3F и

F2 4F .

Под каким

углом надо уста-

новить подкос AB, чтобы после приложения указанных сил узел B не получил горизонтального перемещения? Определить его вертикальное перемещение υB, если АВ = l, площадь поперечного сечения A, модуль упругости Е.

Ответ: arctg 0,75 ;

25

 

Fl

3

 

 

.

EA

3. Из условия прочности стержней ВС и BD определить угол α, обеспечивающий минимальный вес стержней. Размер а задан.

Ответ: / 4.

4. Вычислить величину удлинения стержня от силы F. Площадь стержня меняется по линейному закону: А(х) = A0+ x(A1 – A0)/l.

Ответ: l F l ln A1 / A0 .

E A1 A0

5. Определить напряжения в стержнях 1 и 2 (А1 = A2) и перемещение точки В. Учесть трение в ползуне В (коэффициент трения f). Материал стержней одинаковый.

Ответ: σ1

F

 

1

 

; 2

1 sin ;

A

cosβ fsinβ

 

 

 

 

 

 

 

 

 

 

 

Fl

 

 

 

 

 

sin2 β

δB

 

 

 

 

 

1

 

 

.

EA cosβ

f sinβ 2

2

 

 

 

 

 

22

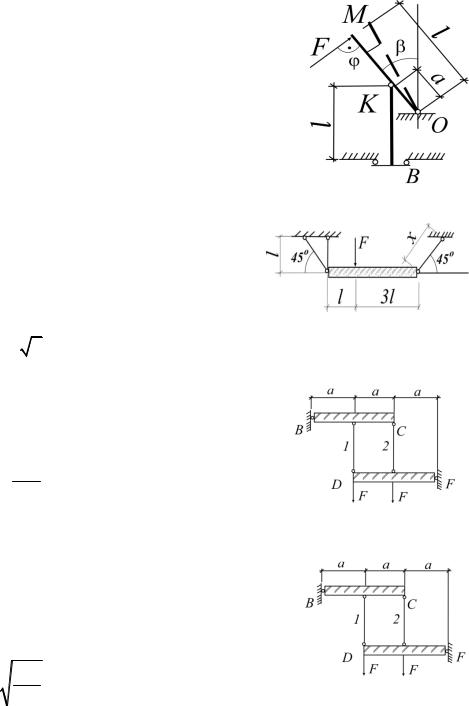
6. Абсолютно жесткий рычаг МО длиной L закреплен в точке К тросом КВ, нижний конец которого может свободно перемещаться по горизонтали. Трос имеет длину l и жесткость поперечного сечения ЕА. Установить зависимость

силы F от угла поворота рычага φ (рис.1.35).

 

 

Ответ: F

2EA a

2

 

 

 

.

L l

sin

sin

sin

2

 

 

 

2

 

7. Aбсолютножесткаябалкаподвешенана

 

 

трех стержнях, поперечные сечения которых

 

 

иматериалодинаковы. Каковадлинаправого

 

 

стержня, если балка под действием силы F

 

 

остается горизонтальной?

 

 

 

 

Ответ: x

2

2 l.

 

 

 

 

8. Стержни ВС и DF абсолютно жесткие.

Дано: E1A1=Е2А2, l1 = l2 = l.

Определить перемещение точки С.

Ответ: с 83 EFlA.

9. Два шарнирно соединенных стержня до приложения силы F горизонтальны. Получить зависимость между силой F и опусканием узла , учитывая, что l l.

Ответ: δ l 3 EFA .

23

Глава 2. НАПРЯЖЕННО-ДЕФОРМИРОВАННОЕ СОСТОЯНИЕ В ТОЧКЕ

Краткие теоретические сведения

Основные понятия и обозначения Упругие постоянные изотропного материала:

,

i коэффициент Пуассона, 0 v 0,5;

i

E модуль упругости при растяжении и сжатии;

G

E

модуль упругости при сдвиге или модуль сдвига.

2 1

i нормальное напряжение в сечении сi-йвнешней нормалью;

i dsi относительная линейная деформация поi-му направлению; dsi

e

dV

x y z

1 2 x y z объемная деформация;

 

dV

 

E

ij касательное напряжение в сечении с i-йнормалью по j-му напр-нию;

ij ji закон парности касательных напряжений, где

 

 

;

i, j

2

 

 

 

ij ij относительный сдвиг или угол сдвига между гранями i и j.

G

Правило знаков: 0, если удлинение; 0, если уменьшение угла 2 .

Линейное напряженное состояние одно из трех главных напряжений отлично от нуля: 1 0;

закон Гука:

1

;

2

1 ;

 

3

1 ;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

E

 

 

E

 

 

E

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

при повороте граней вокруг 2

или 3 ,

 

 

0,

если

:

1,

 

а) напряжения:

 

cos2

;

 

 

 

 

 

 

 

 

sin 2

;

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

1

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

б) максимальное касательное напряжение: max

,

 

 

 

;

 

2

 

1,

 

4

 

в) деформации: 1 cos2

sin2 ;

 

1 1

sin 2

.

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

24

Плоское напряженное состояние два из трех главных напряжений отличны от нуля: 1 0, 2 0;

закон Гука: z

1

z y ;

 

y

 

1

 

y z

; x

 

 

z

y ;

E

 

E

E

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

z

 

yz

 

 

 

 

 

 

 

 

 

0

 

тензор напряжений: Tн

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0

 

;

 

 

 

 

 

 

 

 

 

 

 

zy

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

z

 

 

 

 

 

1

yz

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

тензор деформаций: T

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

2

 

1

0 ;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

д

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

zy

 

 

 

 

 

y

 

 

 

 

 

 

0

2

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

при повороте граней вокруг 3 ,

 

 

 

 

 

 

 

 

 

 

0,

если :

 

 

z ,

 

 

а) напряжения: z cos2 y sin2 zy sin 2 ;

 

 

 

 

 

z

sin2

 

y

cos2

 

 

zy

sin

2 ;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

zy cos 2 ( z

y )

sin 2

;

 

 

 

 

 

 

 

 

 

б) главные напряжения: 2

I

 

 

I

 

 

0,

 

 

 

 

 

2

 

 

 

 

 

 

i

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

где инварианты тензора напряжений 2 ранга

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I1 z y ,

 

 

 

 

 

 

 

 

 

 

 

I

2

 

 

y

2

 

 

 

 

2

 

,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

z

 

 

 

 

 

 

zy

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

или 1,2

z y

1

 

z y 2

 

4 2zy ;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

в) максимальное касательное напряжение:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

max 1

2

 

 

 

1

 

 

 

z

y 2 4 2zy

;

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

zy

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

г) главные площадки: tan 1,2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

,

 

1,2

z , 1,2 0, если ;

 

 

 

 

 

y

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1,2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

д) деформации: z cos2 y sin2 2zy sin 2 ;z sin2 y cos2 2zy sin 2 ;

 

 

zy

cos 2 ( z y )

sin 2

.

2

2

 

 

2

 

Объемное напряженное состояние три из трех главных напряжений отличны от нуля: 1 0, 2 0, 3 0;

закон Гука:

 

1

(

2

 

3

),

i 1,2,3

или i x, y, z;

 

1

 

E

1

 

 

 

 

 

 

 

 

 

 

 

 

 

25

 

 

 

x

yx

zx

1

0

0

 

тензор напряжений: T

 

 

 

xy

 

y

 

 

 

0

 

 

2

0

 

;

н

 

 

 

 

 

zy

 

 

 

 

 

 

 

 

 

 

xz

yz

 

 

 

0

0

 

 

 

 

 

 

z

 

3

 

главные напряжения: 3

I 2 I

 

i

I

3

0,

 

 

 

 

 

 

 

 

 

 

i

 

1

i

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

где инварианты тензора напряжений 3 ранга

 

 

 

 

 

 

 

 

 

 

 

 

 

 

I1 x y z ,

 

 

 

 

 

 

 

 

 

I2 x y y z z x 2xy 2yz 2zx ,

 

 

 

 

 

 

 

 

 

I3

 

x

 

 

 

yx

 

 

zx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

xy

 

 

 

y

 

 

zy

 

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

xz

 

 

 

yz

 

 

z

 

 

 

 

 

 

 

 

 

 

максимальное касательное напряжение: max

1 3

 

 

 

;

 

2

 

, 1,n

3,n

4

 

 

2

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

m

 

 

 

 

 

 

 

 

 

n

1,

 

 

 

 

 

l

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

главные площадки: xyl

 

( y i )m

 

 

 

 

 

zyn

0,

 

 

 

 

 

 

 

 

 

 

yzm

 

 

 

 

z i n 0,

 

 

 

 

 

xzl

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

,

 

 

 

 

 

 

 

 

 

 

;

 

 

 

 

 

 

где l cos x,n ,

m cos y,n

 

 

 

n cos z,n

 

 

 

 

 

 

 

 

 

 

x

1

yx

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

2

zx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

тензор деформаций: T

 

 

xy

 

 

 

y

 

 

 

.

 

 

 

 

 

 

 

 

 

д

 

2

 

 

 

 

 

 

 

 

2

 

zy

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

xz

yz

 

 

z

 

 

 

 

 

 

 

 

 

 

 

 

 

2

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Удельная (в единице объема dV ) потенциальная энергия упругой деформации:

u

1 x x y y z z xy xy yz yz zx zx ;

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

u

1

2x 2y 2z

 

 

 

 

x y y

z z x

1

2xy 2yz 2zx ;

 

E

2G

 

 

2E

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

u

G

e2 G 2x 2y 2z

1 G 2xy 2yz 2zx ;

 

1 2

 

u

 

u

 

 

 

 

u

 

 

 

2

u

 

 

 

 

 

,

 

 

 

;

 

 

 

,

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

i

 

i

 

 

 

ij

 

 

i

 

i

 

 

 

 

ij

 

 

 

 

 

 

 

ij

 

 

 

 

 

 

 

 

 

 

 

ij

 

 

26

Теории прочности:

3 теория прочности или теория max (пластичный материал):

а) общий случай – объемное напряженное состояние: 1 3 R; б) стержень – плоское напряженное состояние, y 0, z , zy :

2 4 2 R;

4 теория или энергетическая теория формоизменения (пластичный материал):

а) общий случай – объемное напряженное состояние:

 

1

 

2

2

2

 

3

2

 

3

2

R;

 

 

 

 

2

1

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

б) стержень – плоское напряженное состояние, y

0,

z ,

zy :

 

 

 

 

 

 

2 3 2

R;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0, 0 ),

k

р

 

 

 

 

теория прочности Мора (при

max

:

 

 

 

 

 

 

 

 

 

 

 

1

 

 

3

 

 

 

 

 

сmax

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

а) общий случай – объемное напряженное состояние:

1 k 3 Rр;

б) стержень – плоское напряженное состояние, y

0,

z ,

zy :

 

 

1 k

 

1 k

2 4 2 Rр.

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

Примечания: 1) осевое растяжение-сжатие стержня линейное напряженное состояние: 1 , 2 3 0 e 1 E2 ;

2) кручение трубы чистый сдвиг, частный случай плоского напряженного состояния: 1 , 2 0, 3 e 0;

3) гидростатическое давление: i p e 3 1 2 p .

E

27

Примеры решения задач

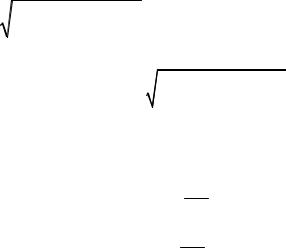
Рис. 2.1

z Ez ,

2.1. Нарастянутойпластинкеустановлены три одинаковых тензометра, как показано на рис. 2.1. Доказать, что показания тензометров связанызависимостью: А+ В= C(l–v), гдеv – коэффициент Пуассона (рис.2.1).

Решение

 

 

 

 

 

 

 

 

2

sin

2

 

 

 

z cos

 

 

;

2

:

 

 

 

z

sin2

cos2

 

 

 

 

 

 

 

 

 

 

 

z 1 ,

где sin2 cos2 1.

 

 

 

i

li , т.к. по условию

l const, то А+ В= C(l – v).

 

li

i

 

 

 

2.2. На боковой поверхности круглого стержня нанесена винтовая линия с углом наклона к образующей α = 60°. Обнаружено, что при осевом растяжении стержня длина винтовой линии не изменилась. Определить коэффициент Пуассона материала (рис.2.2).

Рис. 2.2

Рис. 2.2 (a)

Решение

1 z , 2 3 0:

z cos

2

 

2

0,

 

1

2

 

3

2

 

 

sin

 

 

 

 

 

 

 

0.

 

 

2

2

Ответ: ν 1

 

 

 

 

 

 

 

 

 

 

 

3

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.3. Доказать, что при осевом растяжении (сжатии) стержня абсолютное изменение его объема зависит от длины, но не зависит от площади поперечного сечения этого стержня.

Решение

e x y z VV .

28

 

z

l

 

F

 

 

 

 

 

l

 

EA , x z ,

y z ;

 

 

 

e z 1 2 ll 1 2 VV ,V V ll 1 2 Al EAF 1 2 .

Ответ: V FlE 1 2ν .

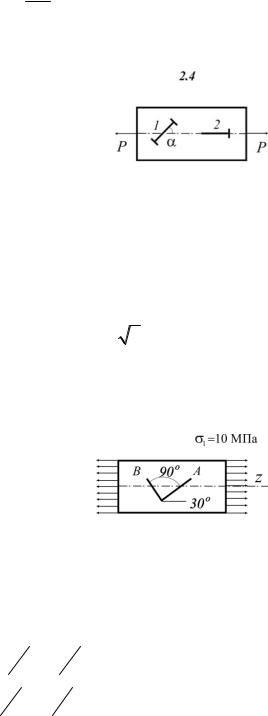
2.4. Под каким углом α к оси стержня надо

установить тензометр 1, чтобы его показания при

растяжении стержня были втрое меньше показа-

ний такого же тензометра 2, расположенного

вдоль оси стержня. Дано: v = 0,33 (рис.2.4).

Рис. 2.4

 

Решение

 

z z cos2 sin2

,

3

 

13 cos2 13 sin2 1 sin2 13 sin2 1 43 sin2 ,

1 3 4sin2 , 4sin

2 2 , sin2

1

 

,

 

sin

2

,

.

2

 

 

2

 

 

 

.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

Ответ:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.5. Определить модуль упругости Е и

 

 

 

 

 

 

коэффициент Пуассона v, если изменения

 

 

 

 

 

 

показаний тензометров А и В, установленных

 

 

 

 

 

 

на образец, как указано на рис. 2.5, равны

 

 

 

 

 

 

соответственно 20 и 2 мм. Коэффициент

 

 

 

 

Рис. 2.5

увеличения тензометров k = 1000, база lT = 100

 

 

 

 

мм (рис.2.5).

 

 

 

 

 

Решение

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

20

 

 

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

0,2 10 3 ,

 

 

 

 

 

 

 

 

 

0,2 10 4 ,

 

 

100 103

 

100 103

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

cos2

30 sin2

30 z

 

 

3

4

1

4

z

2 10 4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

,

 

 

 

 

 

 

 

 

 

z

 

 

,

 

 

 

 

 

 

 

 

 

 

 

 

z

 

 

 

sin2 30 cos2

30

 

 

 

1

 

 

 

 

3

 

 

 

0,2 10 4

 

 

 

 

 

 

4

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

3 1 10

, 29 7,

7 / 29,

z

 

2,9 10 4 ,

 

 

1 3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

29

 

 

 

 

 

z z ,

10 МПа 2,9 10 4 ,

E 105 МПа.

 

 

 

 

 

 

 

E

 

 

Е

 

 

2,9

 

 

Ответ: E 105 МПа/ 2,9,

ν 7 / 29.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.6. Стержень подвергается осевому растя-

 

 

 

 

 

 

 

 

 

жению. Обозначим l1, l2, l3

–

удлинения

 

 

 

 

 

 

 

 

 

трёх, изображенных на рисунке отрезков

 

 

 

 

 

 

 

 

 

равной длины. Доказать, что v (

l1+

l2) + (1 – v)

 

 

 

Рис. 2.6

 

 

 

l3 = 0, v – коэффициент Пуассона (рис.2.6).

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

,

 

 

 

 

Решение

 

 

 

Если

 

то 1 z .

 

 

 

 

 

 

 

 

 

2

 

 

 

 

1

3

 

 

 

Т.к.

 

3

 

z

, то

 

 

2

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

li , т.к. по условию

 

 

 

 

 

 

 

i

l

const, то v (

l1+ l2) + (1 – v)

l3 = 0.

 

 

li

 

 

 

 

 

 

i

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2.8. Однородная пластинка подвергается двухстороннему растяжению. Показания тензометра Т1 в два раза больше показаний тензометра Т2. Коэффициенты

увеличения тензометров одинаковы, а база l2=2l1. Определить коэффициент Пуассона материала пластинки

(рис.2.8).

Рис. 2.8

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2

 

 

1

 

Решение

 

 

 

 

 

 

 

 

 

 

 

80 МПа 40 МПа

 

 

80 40

 

 

2

 

Rl

 

E

 

 

 

 

1

 

 

 

 

 

4

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

40 80

1

2

 

 

 

 

 

40 МПа 80МПа

 

 

 

2

 

2Rl

 

 

E

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4 8 2 2 7 ,

Ответ: ν 2 / 7.

2.9. При совместном действии на квадратный элемент пластины двух одинаковых по величине растягивающих напряжений показание тензометра, установленного по диагонали элемента и имеющего базу L = 100 мм и цену деления шкалы k = 0,001 мм, составило п = 10 делений. Определить показание тензометра после удаления одного растягивающего напряжения, если модуль упругости материала Е = 2 105 МПа и коэффициент Пуассона v = 0,2.

30

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности