Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2381

.pdf

Скачиваний:

Добавлен:

17.06.2024

Размер:

8.13 Mб

Скачать

☆

<<< < Предыдущая 12 / 172 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

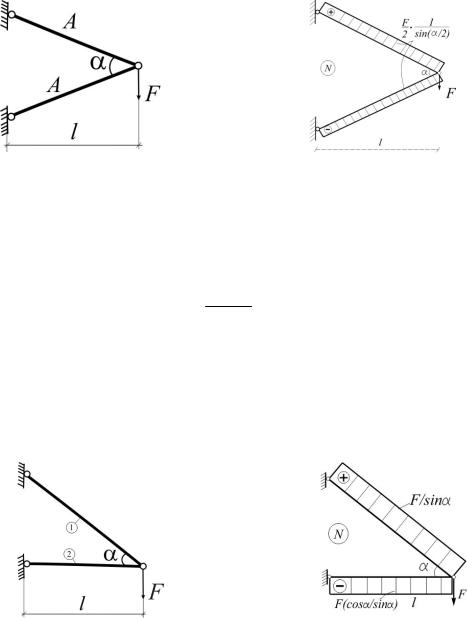
0 2 1 2 4 6 мм.

3 F 3 м

6 мм 200 ГПа 4 см2

, F

213,3 кН.

4 EA

3 м

Ответ: 213,3 кН.

1.13. Определить значение угла α, минимизирующее суммарный объем двух одинаковых стержней, удовлетворяющих условиям прочности. Снижение расчетного сопротивления при сжатии не учитывать. Размер l задан (рис.1.13).

Рис. 1.13

Рис. 1.13(а)

Решение

V A

N l

cos / 2

R cos / 2

2sin / 2 cos / 2

sin

V ' 0 : Fl 1 cos 0 , cos 0. sin2

Ответ: α π2 .

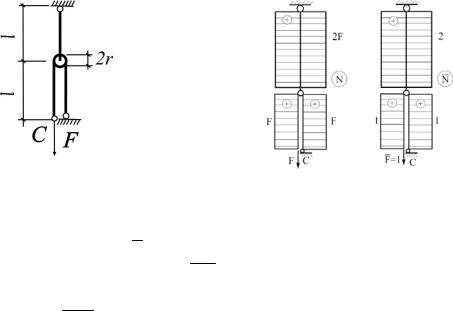
1.14. Определить, при каком угле α объем стержневой конструкции будет наименьшим, если Rs = nRt? Решить задачу для п = 0,5; 1; 5

(рис.1.14).

Рис. 1.14

Рис. 1.14(а)

Решение

Из равновесия узла: N F / sin ;

F cos .

sin

F / sin

;

F / sin

cos A cos .

A l A l

cos l

1 1

2 2

1 cos

cos

2Fl

n cos2

Rt sin

sin 2

cos

V Vmin ,

если V

0 :

2Fl

2cos sin sin 2 n cos2

cos 2 2

0 ,

sin2 2

4sin2 cos2 2 cos2 sin2 (n cos2 ) 0,

cos2 2n cos2 n,

cos2

2n 1

Ответ: cos2 α

; α=600; 550; 480.

2n 1

1.15. ОпределитьвеличинуперемещенияδС послеприложениягруза F, считая радиус шкива r пренебрежимо малым по сравнению с длиной троса l. Площади сечений и материал тросов одинаковы (рис.1.15).

Рис. 1.15 Рис. 1.15(а)

Решение

c NNEA ds EA1 F l 1 2 2F l 2 6EAFl .

Ответ: δс 6EFlA .

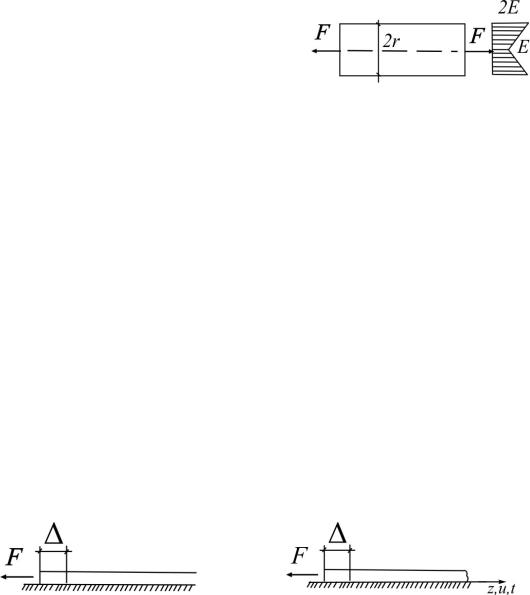
1.16. Круглый стержень диаметром 2r имеет переменный вдоль радиуса модуль упругости, закон изменения которого показан на рисунке. Опираясь на гипотезу плоских сечений, вывести, формулу напряжений в поперечном сечении при осевом растяжении стержня.

Решение

Рис. 1.16

: E

0 r

E 1

E , const .

N dA E

d 2 E 1

2 d E 2

E 2

E 5 r2

F. E

2 3

Ответ: σ E ρ ε σ0 1

, где

σ0

Eε

πr

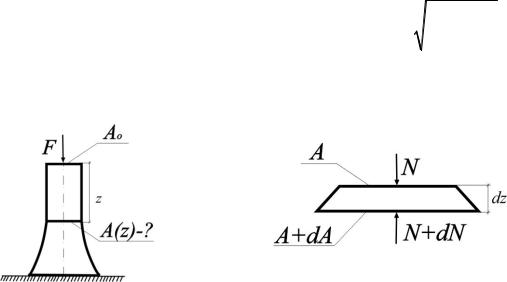
1.17. Очень длинная тяжелая лента лежит на шероховатой по-

верхности и от силы F ее конец перемещается на величину

. Найти

закон изменения нормальных напряжений по ее длине, если погонный вес материала q, коэффициент трения f. Дано: 1) F, А; 2) , Е, А

(рис.1.17).

Рис. 1.17 Рис. 1.17(а)

Решение

1 вариант:

	dN	t qf ,
N z qf z C ,	dz		N 0 F :		С F .

N z F qf z ,	N z			N l 0 : l F / qf .
z			F qf z	, 0 z l .
	A
			A

2 вариант:

t qf ,

N qf z C,

N l 0 :

C qfl .

N z

qf z 2 C z

D qf z 2

, u z

qfl

z D

2EA

1 вариант:

F qf

, l F / qf ;

Ответ: 0 z l :

qf l z

2 EA .

2 вариант:

, l

1.18. Найти закон изменения площади поперечного сечения для бруса равного сопротивления с удельным весом γ от действия осевой силы F. Считать A0 известной величиной (рис.1.18).

Рис. 1.18

Решение

Рис. 1.18(а)

Из равновесия элемента dz :

dN dz A.

Для бруса равного сопротивления с z const:

N A,

N dN A dA ,

dN dA.

Тогда dA dz A,

или

ln A

z C,

при z 0 :

A z A :

C ln A ,

;

ln(

)

Ответ:

A z A

exp

1.19. Определить удлинение конического стержня от собственного веса, а также перемещение произвольного сечения т – п. Удельный вес γ и модуль упругости Е заданы (рис.1.19).

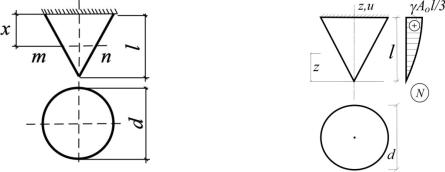
Рис. 1.19	Рис. 1.19(а)
	Решение
x l z ;	0 z l ;

, d dz ,

0 1;

A d 2

; d z d

d ;

d 2 z

A z

A 2

;

dV A z dz A 2

d l ;

dN dV A 2

d l ,

N dN

A0 l

C , N(0)=0: С=0.

N z A

1 A

l 3 .

du dz

N dz

d l2

u du

u 1 0

: D

u 0 l

l D .

u z

z 2

u x

l x

2xl

Ответ: l

; u x

x2 2xl

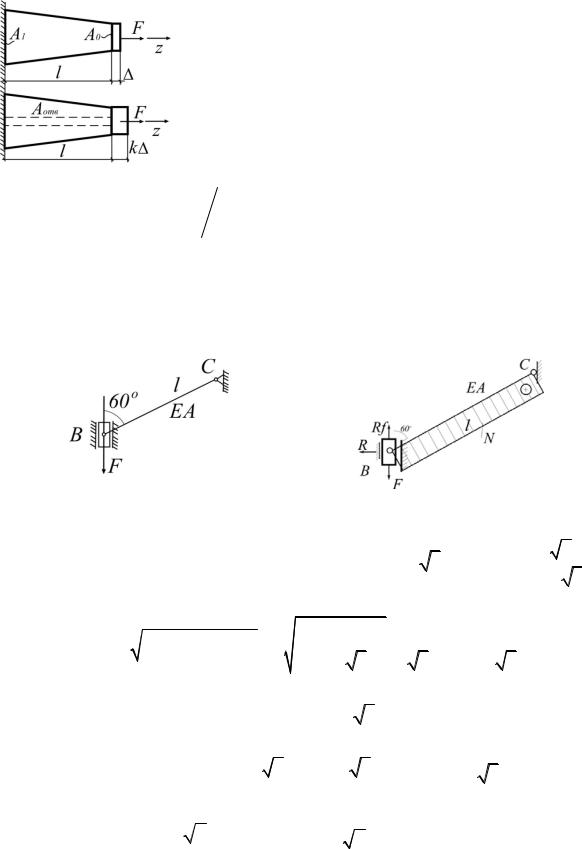
1.21. Стержень с переменной по длине площадью поперечного сечения при действии силы F на конце получает удлинение . Затем в стержне просверливается сквозное отверстие площадью сечения Aотв.

После чего удлинение стержня (от той же силы) вырастает в k раз. Найти площадь Аотв.

Решение

а)

ln A1 / A0

;

б) k

ln A1 Aотв / A0

Aотв

;

A A

в)

A1 Aотв

Aотв

k ln

A A

отв

Ответ: A

k 1

= A

, где

отв

1.22. Определить напряжение в стержне и перемещение точки приложения силы. Учесть трение в ползуне (коэффициент трения f)

(рис.1.22).

Рис. 1.22

Решение

Рис. 1.22(а)

ΣcM 0 : F Rf l sin 600 Rl cos600 ,

F Rf

3 R,

Из равновесия узла В:

F Rf

R 2

f 3

4Fl

1 f 3

1 f

;

4Fl

Ответ:

1 f

3 2

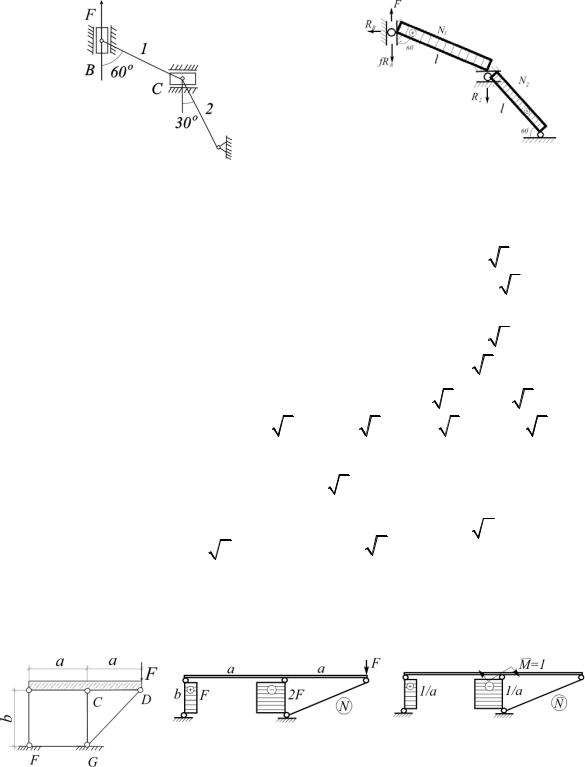
1.23. Дано: l1= l2 = l, А1 = А2 = А, Е1 = Е2 = Е. Определить напряжения в стержнях 1 и 2 и перемещение точки В. Учесть трение

в ползуне В (коэффициент трения f) (рис.1.23).

Рис. 1.23

Рис. 1.23(а)

Решение

Из равновесия:

M лев 0 :

RBl cos60 F fRB

l sin 60 ,

;

1 f

Узел В:

X 0 : RB N1 sin 60 ,

;

X 0 : N1 sin 60 N2 sin 30 ,

Узел C:

N2 N1 3 .

2F 3

2 3

N N

1 f 3

f 3

16Fl

EA 1 f

Ответ:

16Fl

;

2 1 3.

EA 1 f

3 2

A 1 f

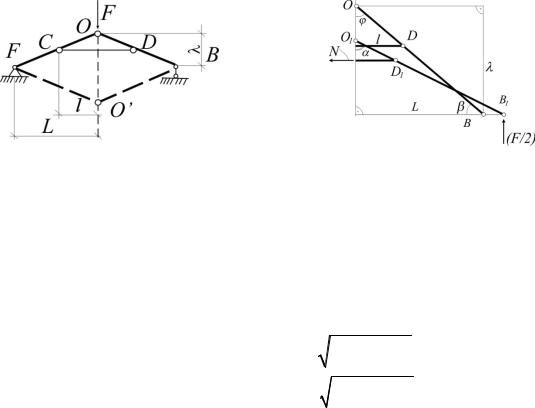
1.25. Абсолютно жесткий брус BCD поддерживается тремя стержнями одинаковой жесткости ЕА. Определить θ – угол поворота бруса BCD при действии силы Р. Дано: а, b (рис.1.25).

Рис. 1.25

Рис. 1.25(а)

Рис. 1.25(б)

Решение

3F b

b 2F b

Ответ: θ 3aEAF b.

1.26. Абсолютно жесткие брусья FO и ВО соединены упругим горизонтальным стержнем CD, жесткость поперечного сечения которого равна ЕА. Считая отношение λ/L << 1, определить наименьшее значение силы F, которую нужно приложить к системе, чтобы вызвать «прощелкивание» из верхнего положения FOB в

нижнее FO'B (рис.1.26).

Рис.1.26

Рис. 1.26(а)

Решение Примечание . Решение задачи методом Мора ошибочно, т.к.

зависимость F( ) нелинейная.

	/ 2 ;
							ctg tg / L;
Из рис.1.26(а):			,		1;		ctg tg / L;
			,		1;
		2
		2
		OD		O D		l 1 / L 2		;
				1	1
						L 1 / L 2
		OB O B				L 1 / L 2		;
				1	1

dl O D sin d O D sinα

O D cos d ;

dN O1D1 sinα

cos d

dN sinα

dN EA ctg d .

M пр 0 :

Из равновесия в деформированном состоянии:

О1

N O D cos

O B sin ,

tg ,

dN dF

tg .

2 l

Тогда dF 2EA ctg2

d ,

2EAl ctg /2

2EA ctg2

2EAl

ctg

где

tg3

tg5

ctg

ctg3

2 EA l

ctg3

Ответ: F

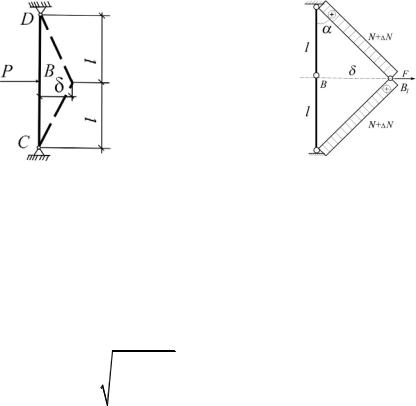
1.27. При сборке двух одинаковых упругих стержней DB и ВС, жесткость сечений которых при растяжении ЕА, созданы начальные растягивающие усилия N. Установить зависимость между приложенной после сборки к шарниру В горизонтальной силой F и его перемещением . Учесть, что l l (рис.1.27).

Рис. 1.27

Рис. 1.27(а)

Решение Примечание. Решение задачи методом Мора ошибочно, т.к.

зависимость F( ) нелинейная.

Из условия равновесия узла B1 в деформированном состоянии:

F 2 N N sin 2 N N l .

l l

l l 1

N l

δ 3

Ответ: F 2 N

1.28.Определить полное перемещение точки В. Е, A, l, P заданы

(рис.1.28).

Рис. 1.28

Рис. 1. 28 (а)

Рис. 1. 28 (б)

Рис. 1. 28 (в)

Решение

N	Ny		ds	1	2F

EA				EA		3
EA				EA		3
N				1
N	N	x	ds	1
		x			0
EA				EA	0
EA				EA

	2l	2		F		l	1	3	Fl

	3		3	3		3	3		EA
	3		3	3		3	3		EA
F		l	1		Fl
			1
	3	3			3EA
	3	3			3EA

B 2Bx 2By	Fl	3 2 1/ 3 2	28	Fl	.
	EA		3
				EA

Ответ: 328 EFAl .

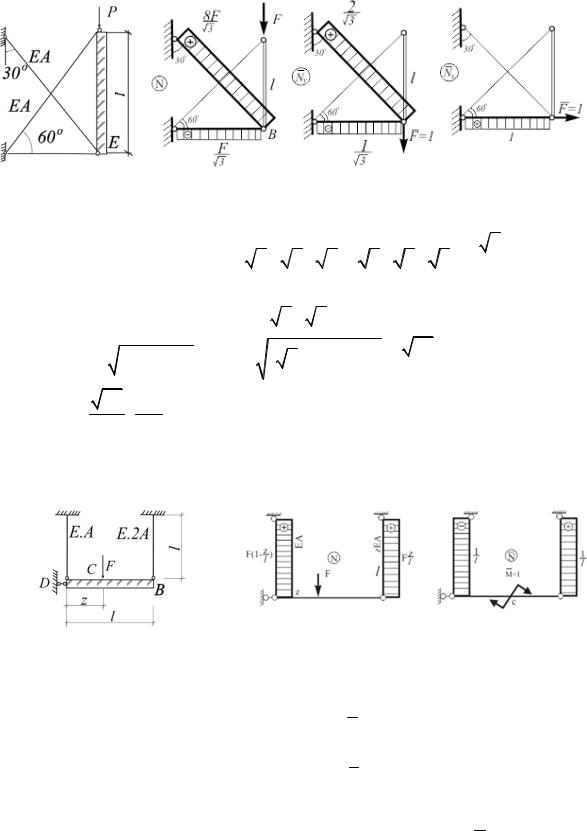
1.29. Найти расстояние z , при котором вертикальное перемещение точки приложения силы F vc = min. E, A, l, F известны. DB – абсолютно жесткий стержень (рис.1.29).

Рис. 1.29	Рис. 1.29(а)
vc vmin , если c 0 .	Решение
vc vmin , если c 0 .

	N1	F			z
			1
			1
					l
				z
				z
N2		F
N2		F		l
				l

N 1

,1 1l ;

N2 l

F 1

E A

2EA

Рис. 1.29(б)

F zl l 1l .

<<< < Предыдущая 12 / 172 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.06.20248.07 Mб02377.pdf
#
17.06.20248.08 Mб02378.pdf
#
17.06.20248.08 Mб02379.pdf
#
17.06.2024243.89 Кб0238.pdf
#
17.06.20248.09 Mб02380.pdf
#
17.06.20248.13 Mб62381.pdf
#
17.06.20248.16 Mб02382.pdf
#
17.06.20248.23 Mб02383.pdf
#
17.06.20248.23 Mб02384.pdf
#
17.06.20248.23 Mб42385.pdf
#
17.06.20248.24 Mб02386.pdf