Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2381

.pdf

Скачиваний:

Добавлен:

17.06.2024

Размер:

8.13 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 1716 17 > Следующая >>>

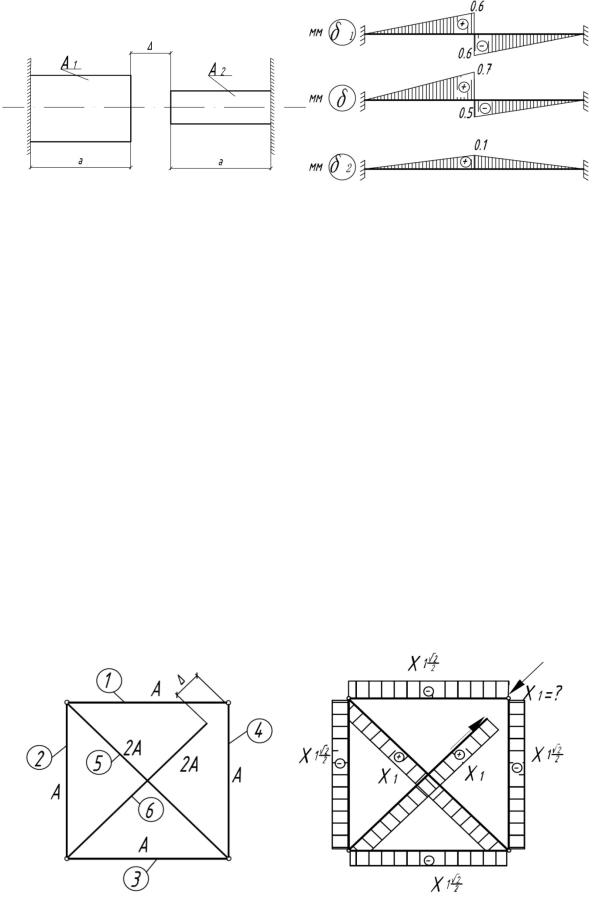
Решение

A B 0;

l1 l2 a;

1) t t1 l1 l2 :

1, 2 мм

48 ;

2 a

12,5 10 6 2 1 м

2) t2 t t1 72 ;

l l

0 :

EA1 EA2

2 E A

12,5 10 6 72 2 200 ГПа 2,5 см2 2 см2

40 кН;

2,5 2

см2

Xl1

12,5 10 6 72 1 м

40 кН 1 м

0,1 мм.

200 ГПа 2,5 см2

Ответ: 1) δС1

0,6 мм вправо; δС2

0,6 мм влево;

2) δС1

0,7 мм вправо; δС2

C 0,5 мм влево.

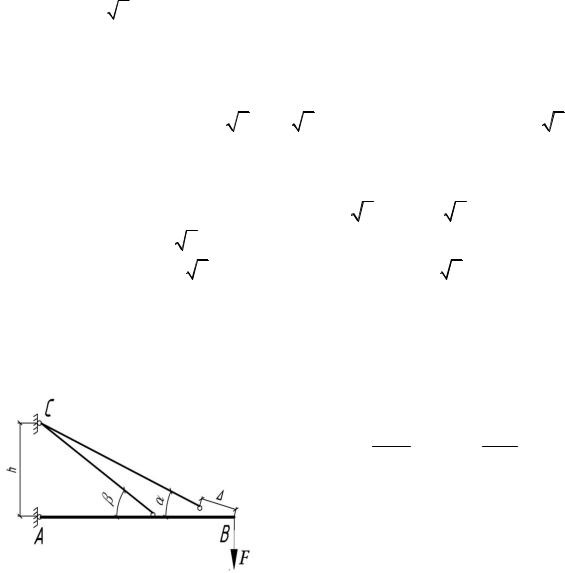
6.36. Определить монтажные напряжения в стержнях, если один из диагональных стержней сделан на 0,1% короче проектного размера.

151

Решение

l l	2	,	A A,	i 1, ,4;	l l,	A 2 A,	i 5,6.

i	2		i		i	i

0,1 10 2l.

Система один раз статически неопределима: 11X1 1F .

									1			2					2	2		1								1 2
		N	N						1			2					2	2		1			2					1 2

11 EA						ds		EA		l 2					1		2		4	E2A l 1					2 EA l;
				i

													1F						EA			EA							Ni
1F	N N				ds 0;				X1				1F						EA			EA				3			Ni
																				l				10			.	i		.
		EA																	1 2	l		1 2		10			.	i	A	.
			i													11													i
Ответ: σi							E		2		10			3		, i	1, ,4; σi					E			10		3	, i 5,6.
Ответ: σi							2 1		2		10					, i	1, ,4; σi				2 1 2				10			, i 5,6.

6.37. Определить величину монтажного зазора ∆ из условия, чтобы усилие в стержне ВС после монтажа и приложения силы F стало равным нулю. Материал и сечения стержней одинаковы и заданы, размер h и величины углов α и β считать известными.

Решение

l sinh ; l sinh .

По условию N 0.

M 0 :

N F

;

tan

hcos

tan cos

F 1

2Fh

cos2

N N

tan cos

cos

sin 2 sin

B sin .

	2Fh		cos2 α
Ответ:	EA				.

		sin 2β sinα		cosβ

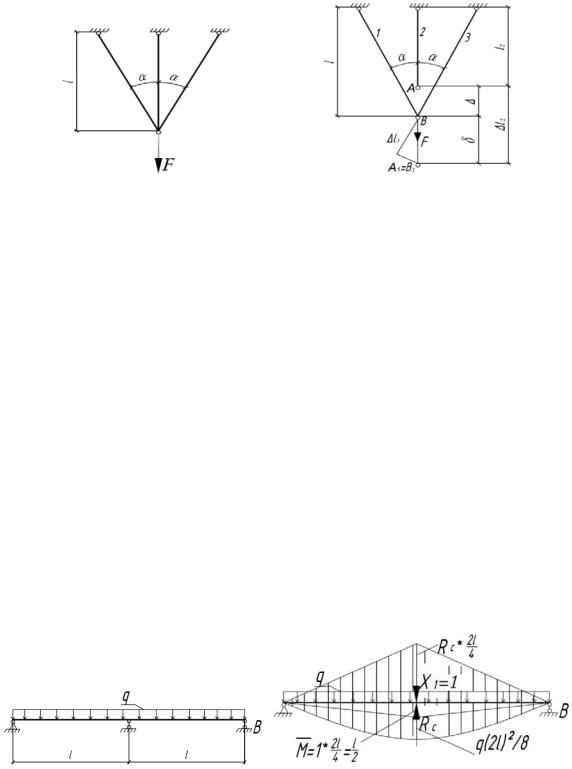
6.39. Определить величину монтажного зазора ∆ среднего стержня, при которой после монтажа и приложения силы F нормальные напряжения во всех стержнях были бы равными. Сечения стержней одинаковые. Угол и размер l считать заданными.

152

Решение

	l2 l ,	l1 l3 l / cos .
Статика: i const,	Ni i Ai const;

Y 0 :

2N1 cos N2 F,

1 2cos

Геометрия: l

cos ,

;

cos

Физика:

N1 l1

F l / cos

;

2cos EA

1 2cos EA

1 2cos

cos

1 2cos EA

cos

tan2 α

Ответ:

1 2cosα

1 F / EA 1 2cosα

1 2cosα

т.е. на увеличить длину среднего стержня.

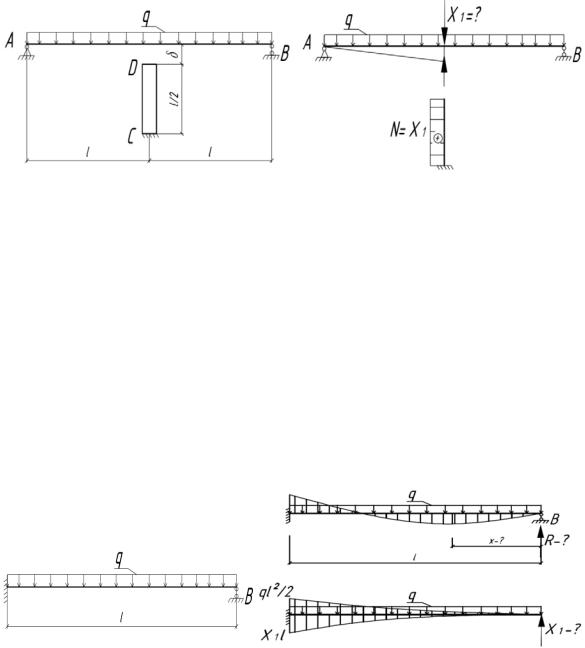
6.40. Определить величину осадки средней опоры C , при которой

изгибающие моменты над этой опорой и в серединах пролетов равны по модулю.

Решение

A B 0.

Из симметрии: RA RB .

Y 0 :

2RA RC 2ql.

По условию:

q l / 2 2

M l M

R l ql2

, R

ql.

153

Тогда R

14 ql, M

M l ql2 .

2 q 2l

M M ds

5 l

14 ql

3 8

8 2 3 12

4 2

72EI

ql4

Ответ: На C

вниз.

72EI

6.41. Доприложениянагрузкиq междубалкойАВистойкойCD имеется зазор . Какова его величина, если после нагружения изгибающий

момент в середине балки АВ оказался равным нулю? Материал стержней АВ и СD одинаков.

Решение

A B 0.

Из симметрии: RA RB.

Из равновесия: 2RA RC 2ql.

По условию M

0 :

R l

ql2

ql.

R ql.

2 ql

1 1 2l

M M

ql 1 .

EAo

3 8

2 4

EAo

Ответ: δ

ql4

ql2

24EI

2EA

6.43. Для балки постоянного по длине поперечного сечения определить величину предварительного смещения опорного сечения В, при котором вес балки будет наименьшим.

154

A 0,

Решение

A 0.	По условию: M A MC :			RBl ql2		RB x qx2 .
	RB				2	2
0 : x		. RB2	RB 2ql ql 2	0,	RB	2 1 ql.

	q

			1 l			1 ql2
B	M M	ds			RBl 1l l
	EI
			EI	3		3 2

Ответ: На B ql4 0,0131 вверх.

3	1l	ql4	2 1	1
		EI			.
4			3	8

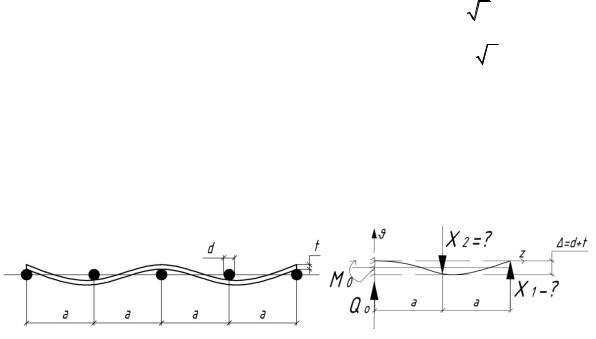
6.44. Через пять равноудаленных друг от друга роликов диаметров d, центрыкоторыхлежатнаоднойпрямой, протянутаполосатолщиной t=d и шириной b. Определить давление полосы на ролики, если d а.

Решение

Начало координат на оси симметрии.

0 0, 0 0, M0 X1 2a X2 a, Q0 X1 X2.

Универсальное уравнение изогнутой оси балки:

	EI z											z	2			z	3					z a			3
						M						z		Q		z		X				z a				.
						M					2			Q				X						6		.
										0	2			0 6							2			6

a 2d :	2d EI M										a2			Q	a3			,		2d EI X										5a3	X			2a3		;
									0		2			0	6													1		6		2		6
2a 0 :	0 M		2a 2					Q					2a 3		X					a 3			,	0		X			16a3		X				5a3	.
2a 0 :	0 M		2					Q							X								,	0		X				6	X				6	.
		0	2								0			6					2	6							1			6			2		6
Ответ: F F X				1		60 EId									,т.е. вниз;
1	5			1						7				a3
										7				a3
F	F X				2	192 EId									, т.е. вверх;
2	4				2				7					a3
									7					a3
F	2Q		264 EId , т.е. вниз.
3		0					7					a3
							7					a3

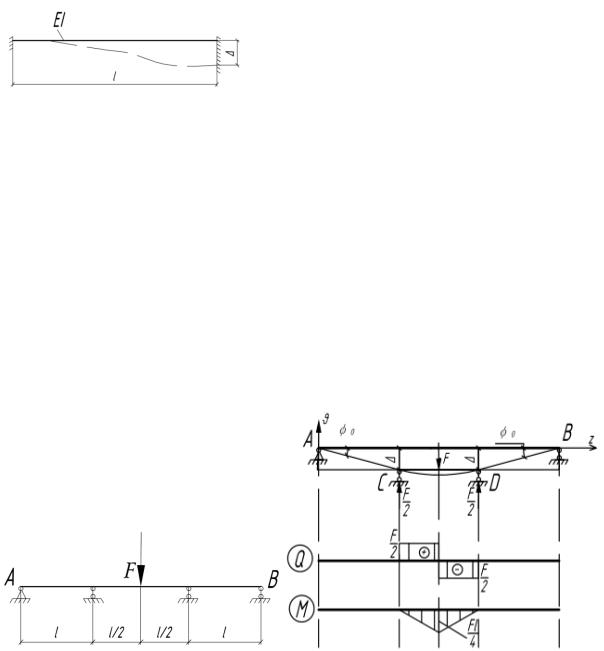
6.45. Балка защемлена обоими концами. Одна из опор получает линейное смещение ∆=0,004l. Считая EI const , найти угол поворота

среднего сечения.

155

																			Решение
																			0 0,		0 0.
														Универсальное							уравнение изогну-
											той оси балки:
		EI z M						z2		Q		z3		;		EI z M				z Q				z2	.
		EI z M					2			Q		6		;		EI z M				z Q				2	.
						0	2				0	6		l2			l3 ,		0			0		2
	l :					EI					M			l2		Q	l3 ,		M					6EI		;
													0 2			0	6				0			l2
	l 0 :										0 M					l Q		l2 ,		Q			12EI .
															0		0	2			0			l3
Ответ: φ	l		1	M			l		Q		l /		2 2				3		0,006				рад, т.е. .

	2		EI				2					2					2
	2		EI		0		2			0		2					2		l

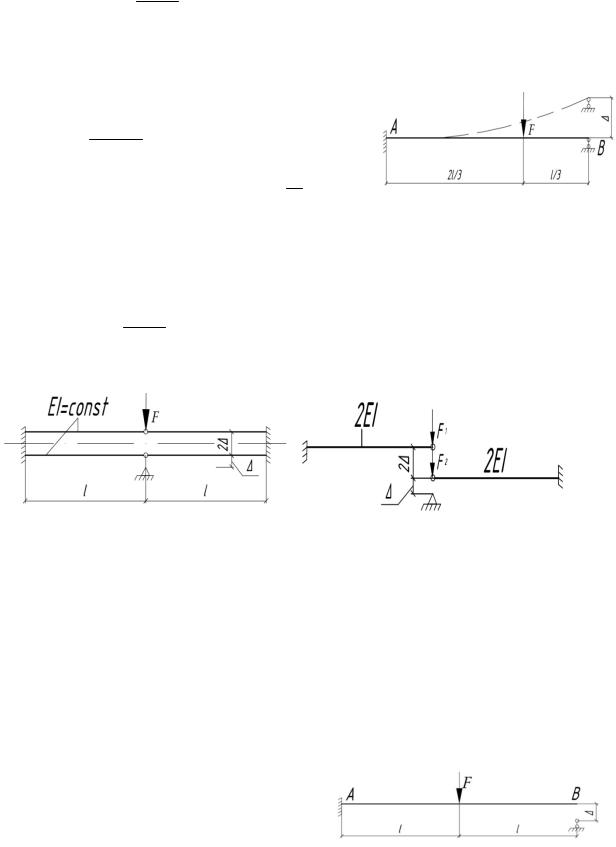
6.46. На какую величину ∆ необходимо опустить средние опоры балки постоянного сечения, чтобы изгибающие моменты в сечениях надэтимиопорамиобратилисьвнуль? ПостроитьэпюрыQ, Мподлине балки.

Решение

Деформация системы симметричная.

По условию над средней опорой MC RA l 0, т.е. RA 0 :

в крайних пролетах M 0, Q 0

0 l.

0, M

0; R

Универсальное уравнение изогнутой оси балки:

EI z EI

z l 3

EI z EI

z l 2

;

156

			F	l / 2	2		2
3 l	0 :	0 EI 0			,	EI 0	Fl .

			2	2
2							16

Ответ: Fl3 , т.е. вниз.

16EI

6.47. На какую величину ∆ надо поднять опору В, чтобы нормальные напряжения в сечении А были равны нулю?

Решение: По условию 0 : M A 0,

тогда RA F ll / 3 F3 .

0 0, 0 0, M0 0, Q0 F3 .

Универсальное уравнение изогнутой оси балки:

EI z Q	z	3	F	z 2l / 3	3	. l :	EI	F l	3	F	l / 3	3
	z			z 2l / 3				F l			l / 3	.
	6			6
								3 6			6
0								3 6			6

Ответ: 4Fl3 .

81EI

6.48. Определить работу силы F, приложенной к верхней балке, к моменту, когда нижний шарнир коснется земли. Считать ∆ l.

Решение

F F1 F2;

Fi Fi i .

EIi 2EI.

F l

F l3

6EI

3EI 2

консольная балка:

, F

; A

i i

3EIi

6EI

2 3 :

1 ,

2 2 ;

A A

A 3EI 12

3EI 22

3EI 3 2

3EI 2 .

30EI

Ответ: A

6.49. При какой величине смещения опоры ∆ реакция правой опоры будет в четыре раза меньше, чем в заделке?

157

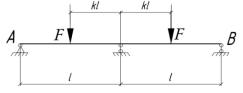
Решение

По условию RA 4RB 54 F, тогда M A RB 2l F l .

0,	0,			M		0	3 Fl,					Q 4 F.
0	0					0				5		0	5
										5			5
Универсальное уравнение изогнутой оси балки:
EI z M			z	2	Q			z	3		F z l		3
			z					z					.
			2					6					.
		0	2				0	6				6

2l :	EI		3 Fl			2l 2					4 F	2l 3	F l3	3Fl3	.
2l :	EI		3 Fl				2				4 F	6	F l3		.
			5				2				5	6	6	10EI

Ответ: 0, 3 Fl3 вниз.

6.50. Определить величину необходимой осадки ∆ средней опоры, при которой объем балки постоянного поперечного сечения будет наименьшим.

Решение

Деформациясистемы симметричная.

A 0; C , C 0.

2RA RC 2F. Mпр RA l 1 k .

MC RAl Fkl.

По условию:

пр

;

4F 1 k .

2 k

Q R F

Универсальное уравнение изогнутой оси балки:

EI z EI z R

z l kl

EI z EI R

z l kl

A 2

l 0 :

0 EI 0 RA l2

kl 2 ,

EI 0 Fl2

k k 1 2

2 k

l :

EI Fl2

k k 1 2

l F

F kl 3 .

2 k

Ответ:

Fl3

k k3 5k2 6k 2

, если 0, то вверх.

6EI

2 k

158

, т.е. вниз.

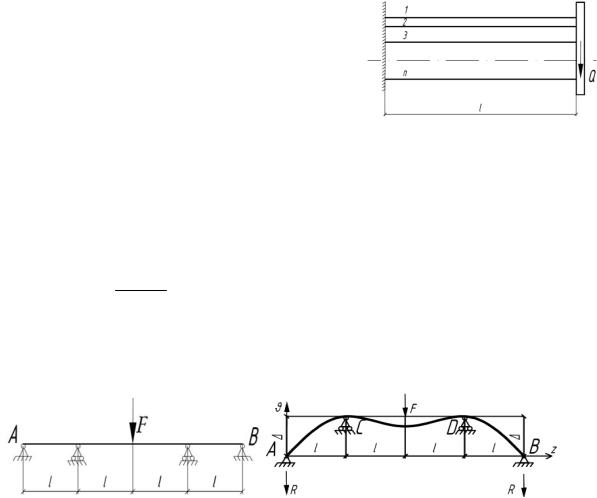
6.51. Плоская плита весом Q удерживается с помощью n одинаковых стержней длинной l, которые жестко соединены с плитой. Опре-

делить вертикальное перемещение плиты под действием веса Q.

Решение
0,	0,		Q Q .
0	0			0
Универсальное уравнениеn изогнутой
оси каждой -ой балки:
EI z M			z2	Q	z3		.		EI z M						z Q	z2	.
EI z M			2	Q			.		EI z M						z Q	2	.
		0	2	0	6					l2 ,				0	0	2
l 0 :				0 M			l	Q		l2 ,		M		Ql .
						0			0	2			0		2n
l :				EI Ql					l2		Q	l3		Ql3 .
								2n		2	n	6			12n

Ответ: Ql3

12nEI

6.53. На какую величину ∆ необходимо поднять средние опоры, чтобы при нагружении системы силой F углы поворота сечений над этими опорами были равными нулю? Изгибная жесткость сечения балки постоянна и равна EI.

Решение

Деформация системы симметричная.

A 0;

C , C 0;

пр 0.

2RA

2RC F.

RA R,

RC R F / 2.

Универсальное уравнение изогнутой оси балки:

EI z EI

z l

z R

. EI z

A 6

A 2

l 0 :

0 EI 0 R l2 ,

EI 0

Fl2

;

2l 0 :

0 EI R 2l 2 R l2 ,

;

C 2

l :

EI EI 0l R l3

Fl3 .

Fl3

Ответ: На

вверх.

12EI

159

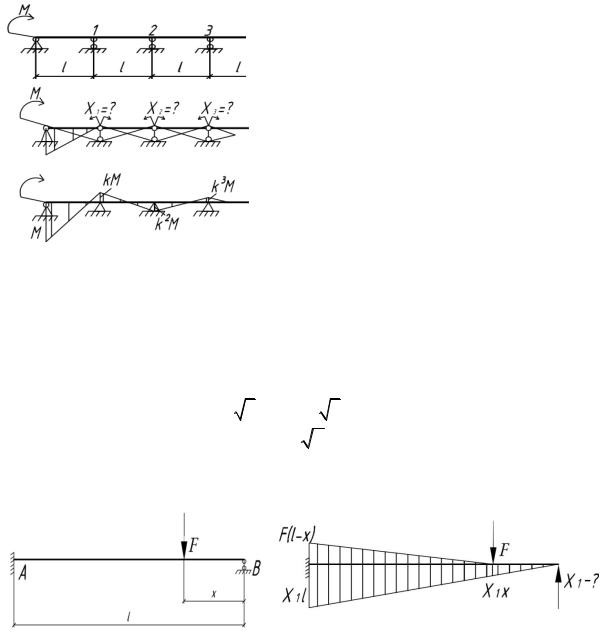
6.54. Построить эпюру изгибающих моментов для неразрезной балки с бесконечным числом пролетов, загруженной на левом конце моментом M. Все пролеты имеют одинаковую длину l и жесткость EI.

Решение

OC MC разрезнаябалка:

ij X j iF 0,

i 1, , ,

j 1

i M j

ds :

i j;

6 ,

iEI

F ds :

, i 1;

, i j 1;

4X1 X2 M 0,

i 1;

Xi 1 4Xi Xi 1 0,

i 2, , .

Обозначим X0 M :

Xi 1 4Xi Xi 1 0,

i 1, , .

Так как Xi 1 k Xi ,

где i 0,1, , , причём

1 k 0.

Тогда Xi 1 1 4k k2 0,

i 1, , .

k 2 3 2 3 0,268.

Ответ: Mi 1 k Mi ,

k 2 3 0,268,

i 0,1, , .

6.55. Сила Р может находится в любом месте балки АВ. При каком значении х изгибающий момент под силой F будет максимальным?

Решение

Система один раз статически неопределима: 11X1 1F

F l x 2

; 1F

M M

l x

;

3EI

2EI

l x

2l x .

M X1 x

l x

2 2lx x2 .

M 0 :

2 l x 2lx x2

l x 2 2l 2x

160

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 1716 17 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.06.20248.07 Mб02377.pdf
#
17.06.20248.08 Mб02378.pdf
#
17.06.20248.08 Mб02379.pdf
#
17.06.2024243.89 Кб0238.pdf
#
17.06.20248.09 Mб02380.pdf
#
17.06.20248.13 Mб62381.pdf
#
17.06.20248.16 Mб02382.pdf
#
17.06.20248.23 Mб02383.pdf
#
17.06.20248.23 Mб02384.pdf
#
17.06.20248.23 Mб42385.pdf
#
17.06.20248.24 Mб02386.pdf