
2381
.pdf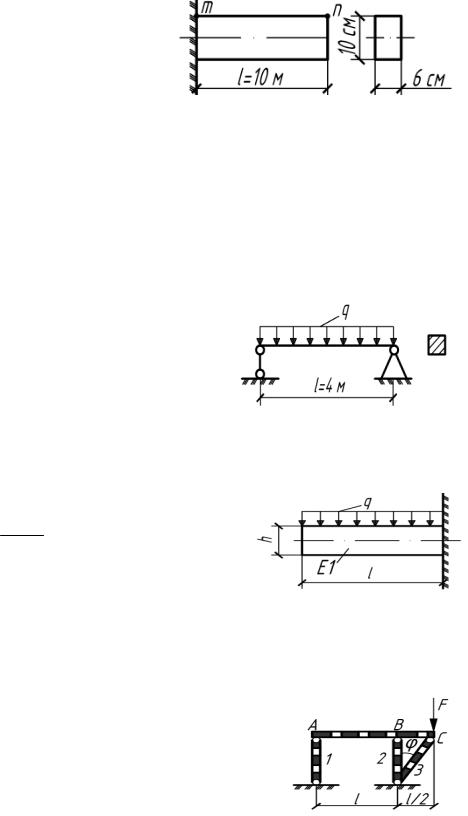
5.14. Стальная балка изгибается под действием собственного веса. Найтидеформациюверхнеговолокнатп, еслинаибольшеенапряжение в балке равно 240 МПа, а Е = 200 ГПа (рис.5.14).
Ответ: lmn 4 мм удлинение.
5.18. От момента M = 100 Hм, приложенного на конце консоли l = 2 м, в среднем сечении = 0,04 рад. Определить радиус кривизны оси балки и прогиб на свободном конце.
Ответ: ρ 25 м; max 8 см вниз.
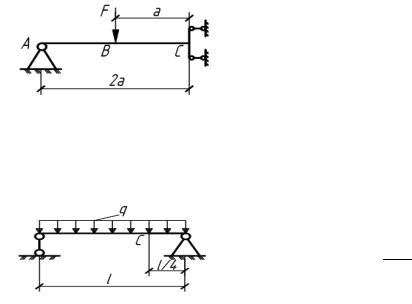
5.21. Балка квадратного сечения находится под действием распределенной нагрузки q = 8 кН/м. Определить максимальный прогиб балки и радиус кривизны оси в среднем се-
чении, если в этом сечении σmax 12 МПа,
а модуль упругости Е= 10 ГПа.
Ответ: max 2 см; ρ 83, 3 м.
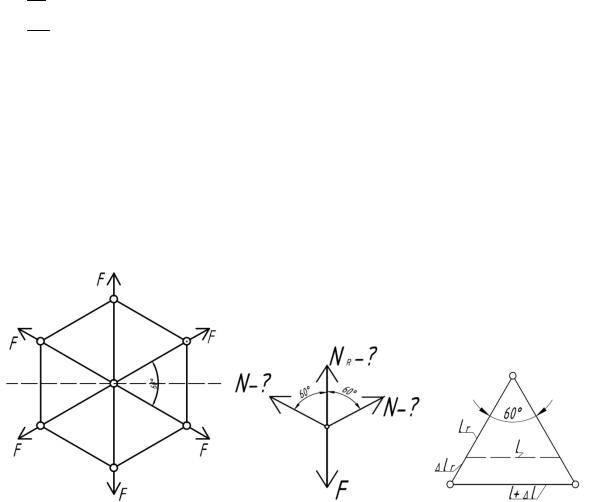
5.35. Найти, чему будет равна разность между длиной верхнего и нижнего волокон балки после изгиба, вызванного нагрузкой q.
Ответ: lВН ql3h .
6EIx
5.51. Стержень ABC с постоянной жесткостью EI шарнирно закреплен на абсолютно жестких стержнях 1, 2 и 3. Определить вертикальное и полное перемещение шарнира С при действии силы F.
Ответ: Y |
Fl3 |
вниз; |
|
Y |
|
Fl3 |
. |
|
8EI |
sinφ |
8EI sinφ |
||||||
|
|
|
|
|||||
131
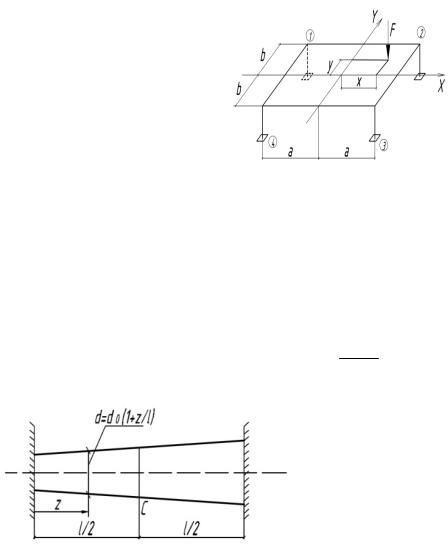
5.58. Найти прогиб сечения В и опорный момент Мс. Жесткость балки постоянная.
Ответ: B |
4 |
|
Fa3 |
вниз; MC Fa. |
|
3 |
EI |
||||
|
|
|
5.62. Определить прогиб балки в точке С, если заданы l и угол поворота на левой опоре.
Ответ: C φAl 25657 .
132
Глава 6. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ
Краткие теоретические сведения Основные понятия и обозначения
СОС статически определимая система, т.е. геометрически неизменяемая система, вкоторойвнутренниеусилиямогутбытьопределеныизуравнений равновесия (уравнений статики).
СНС статически неопределимая система, т.е. система, в которой внутренние усилия нельзя найти только из одних уравнений равновесия (уравнений статики). Для определения внутренних усилий в СНС необходимо рассмотреть три стороны задачи: 1) статическая устанавливает связь между внешней нагрузкой и внутренними усилиями, т.е. рассматривает уравнения статического равновесия; 2) геометрическая устанавливает связь между перемещениями и деформациями элементов системы, т.е. уравнениясовместностидеформаций; 3) физическая устанавливаетсвязь между усилиями и деформациями, при упругой деформации из закона Гука.
Примечание: При заданном по условию распределении внутренних усилий в СНС, решение задачи возможно без раскрытия статической неопределимости.
лишняя связь дополнительная связь в СНС по сравнению со СОС;
степень статической неопределимости разность между числом искомых усилий и числом независимых уравнений равновесия, т.е. число лишних связей;
МС метод сил, т.е. один из методов расчета СНС по схеме:
1) отбрасываютсяi-елишниесвязи, вместонихприкладываютсялишние неизвестные усилия X i (при этом заданная СНС СОС, т.е. получаем ОС
(основную систему) МС); 2) разрешающие (канонические) уравнения для усилий Xi уравнения совместности деформаций заданной СНС и
ОСМС, это, какправило, отсутствиеперемещенийвОСМСпонаправлению отброшенной в СНС i-й лишней связи.
|
1 |
|
|
м |
|
|
k |
|
податливость упругой опоры k от единичной силы, |
k |
|
|
; |
rk |
|
|||||
|
|
|
Н |
|
||
|
1 |
|
|
Н |
|
rk |
|
жесткость опоры k от единичного смещения, |
rk |
. |
|
k |
|||||
|
|
|
м |
Определение перемещений в СНС по формуле Мора, например от N :
|
|
|
N |
|
|
|
|
N o |
N o |
N |
|
|
||
|
|
N |
F |
|
|
N |
F |
|
||||||
iF |
|
i |
ds |
|
i F |
ds |
|
i |
ds , |
|||||
|
EA |
|
|
EA |
|
EA |
|
|||||||
где iF проекция полного перемещения на i-е направление от внешней нагрузки F (причина) в заданной СНС;
133
NF , Ni "грузовая" и "единичная" эпюры N в заданной СНС;
NFo , Nio "грузовая" и "единичная" эпюры N в любой СОС, из СНС.
Примечание: iF от внутреннихусилий Mx , My ,T определяется анало-
гично.
Примеры решения задач
6.1. Определить усилия в стержнях плоской фермы, загруженной в узлах радиальными силами F. Жесткость ЕА всех стержней одинакова (рис.6.1).
Рис. 6.1 |
Рис. 6.1(а) |
Рис. 6.1(б) |
|
Решение |
|
а) Статика. Из равновесия: Y 0 : F Nr 2N cos60 Nr N.
б) Геометрия. lr l, |
равностороннийтреугольник . |
|||||||
в) Физика. lr |
Nrlr |
|
|
Nrl |
, |
l |
Nl |
. |
|
EA |
|
||||||
|
EAr |
|
|
|
EA |
|||
Ответ: Nr N F / 2.
6.2. Абсолютно жесткая плита опирается на четыре стойки одинаковой длины L и одинаковой площади поперечного сечения А. Определить усилия в стойках от нагрузки F, пренебрегая собственным весом плиты и считая, что опорные устройства позволяют стойкам воспринимать растягивающие усилия.
Решение
Из симметрии XY главные центральные оси составного стержня из 4 одинаковых стоек.
N F; |
M y F x; |
Mx F y. |
134
|
По |
|
принципу |
|
|
суперпозиции |
|
согласно |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Г.П.С.: |
|
N |
|
|
|
|
M y |
|
|
M |
|
|
|
|
F |
|
Fx |
|
|
|
Fy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Ni |
|
|
|
|
x |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
4 |
|
|
4xi |
|
|
|
4 |
4xi |
|
4 yi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
4 yi |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
где x1 a, |
|
y1 b; |
|
|
|
|
|
|
x2 a, |
|
y2 b; |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
x4 a, |
|
y4 b; |
|
|
|
|
|
|
x3 a, |
|
y3 b. |
|
|
|
|
|
|
|||||||||||||||||||||||||
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
N1 |
|
F |
1 |
|
|
x |
|
y |
; |
|
|
|
N2 |
F |
1 |
|
x |
|
|
y |
|
; |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
4 |
|
a |
|
|
|
|
|
a |
|
|
b |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
N4 |
F |
|
|
|
|
x |
|
y |
|
|
N3 |
|
|
F |
|
|
|
|
|
|
|
x |
|
y |
||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
; |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
. |
||||||||||||||||
|
|
|
|
4 |
|
a |
|
|
|
4 |
|
a |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
||||||||||||||
6.3. Определить допускаемое повышение температуры стального бруса конической формы и перемещение среднего
сечения С. Дано: R = 250 МПа, l = 96 см, αt = 12,5 10 6
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
2 , |
|
|
|
|
|
|
||||||||||||||
|
|
|
d z d |
0 |
1 |
z |
, |
A z A |
1 |
z |
A d02 |
; |
|||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
0 |
|
|
l |
|
0 |
4 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N z |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
lt t t l; |
|
X const; |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
l |
|
N z dz |
|
|
|
|
|
|
Xl |
|
|
|
|
l l |
|
|
Xl |
|
|
|
||||||||
|
|
|
|
lN |
|
|
|
|
|
|
|
|
|
|
|
|
|
; |
|
||||||||||||||
|
|
|
|
|
|
EA z |
EA |
|
l z |
2EA |
|
|
|||||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
0 |
0 |
|
|
|
||||
|
|
|
|
l l |
l |
N |
|
t |
t l |
Xl |
|
; |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
2EA0 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
X |
|
|
|
l 0 : |
R |
|
X 2 t t EA0. |
|
|
|
|
|
|
|||||||||||||||||
|
max |
|
R : |
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
250 МПа |
|
|
|
||||||||||||
A |
|
|
|
|
2 |
t |
|
E |
|
2 12,5 10 6 |
200 ГПа |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 .
град
50 С.
135
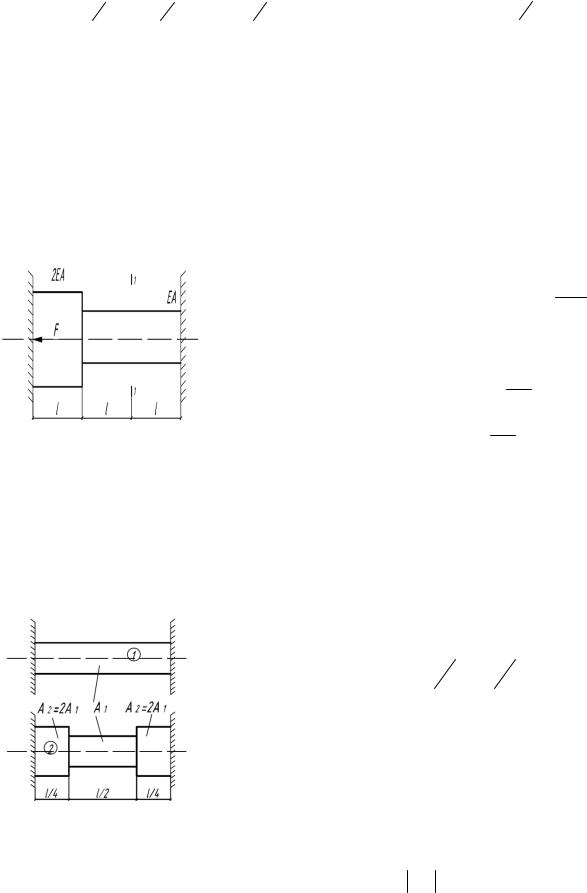
l 2 |
|
|
l 2 |
|
l 2 |
X dz |
|
Xl |
|
l l 2 |
|
|||
С dz t t dz |
|
|
t t z |
|
|
|
|
|
||||||
EA z |
EA |
l z |
||||||||||||
0 |
|
|
0 |
|
0 |
|
|
|
0 |
|
|
0 |
|
|
t t |
l |
|
Xl |
t t |
|
l |
12,5 |
10 6 50 96 |
см |
0,1 мм. |
|
|||
2 |
3EA0 |
6 |
6 |
|
||||||||||
Ответ: t 50 С; |
δС 0,1 мм влево. |
|
|
|
|
|
||||||||
6.4. Брус, жестко защемленный по концам, равномерно нагрет по всей длине на t и нагружен силой F. Полагая размеры бруса,
температурный коэффициент линейного расширения и модуль упругости известными, определить, при каком значении силы F сечение I–I останется неподвижным.
Решение
|
|
|
|
|
|
|
|
|
|
а) l |
|
t 3l; |
l |
X |
|
|
X Al |
|
X A 2l |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
t |
|
|
|
|
|
2EA |
|
EA |
||||||||
|
|
|
|
|
|
|
|
|
|
|
l l |
X |
l |
F |
0 : 3 |
tl 5X Al |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
t |
|
|
|
|
|
2EA |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X Al |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
б) l |
|
t l; |
l |
X |
|
|
; |
|
l |
F |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
t |
|
|
|
|
|
|
|
|
EA |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X Al |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
l l |
X |
l |
F |
0 : |
|
|
|
tl |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
t |
|
|
|
EA |
|
|||||
|
|
|
5 |
|
|
Fl |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
в) t tl |
3 |
|
2 |
|
|
|
|
2 |
|
2 |
0, |
F |
t tEA. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
EA |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: F αt tEA.
; lF FEA2l ; 2EAFl 0.
EAFl ;
EAFl 0.
6.5. В каком из двух стержней (1 или 2) возникает большее напряжение σt , вызванное охлаждением каждого стержня на t ?
Каково отношение σ1 / σ2,max ?
|
|
|
|
|
Решение |
|
|
|
|
|
||||||||
1) t N 0 : |
|
|
|
|
1 E1 t t; |
|
|
|
||||||||||
2) l l |
|
0 : |
tl 2 |
N l |
4 |
|
N l |
2 |
0, |
|||||||||
N |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|||||||||||||
t |
|
|
|
t |
|
|
|
E2 A2 |
E1A1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
N |
4 E A |
t, |
|
|
|
2,max |
|
N |
|
4 E |
t. |
|||||||
|
|
A |
|
|||||||||||||||
|
3 1 1 |
t |
|
|
|
|
|
|
|
|
3 |
|
1 t |
|
||||
|
|
|
σ1 |
|
|
3 . |
1 |
|
|
|
|
|
|
|
||||
Ответ: |
|
|
|
|
|
|
|
|
|
|
|
|||||||
σ2,max |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||
6.6. Длины участков стержня а, b и с могут изменяться так, чтобы а+b+с = const. При некоторых значениях длины с, изменяя
размеры а и b, можно добиться, чтобы N1 N2 . Установить, для
каких длин с возможно выполнить это условие.
136
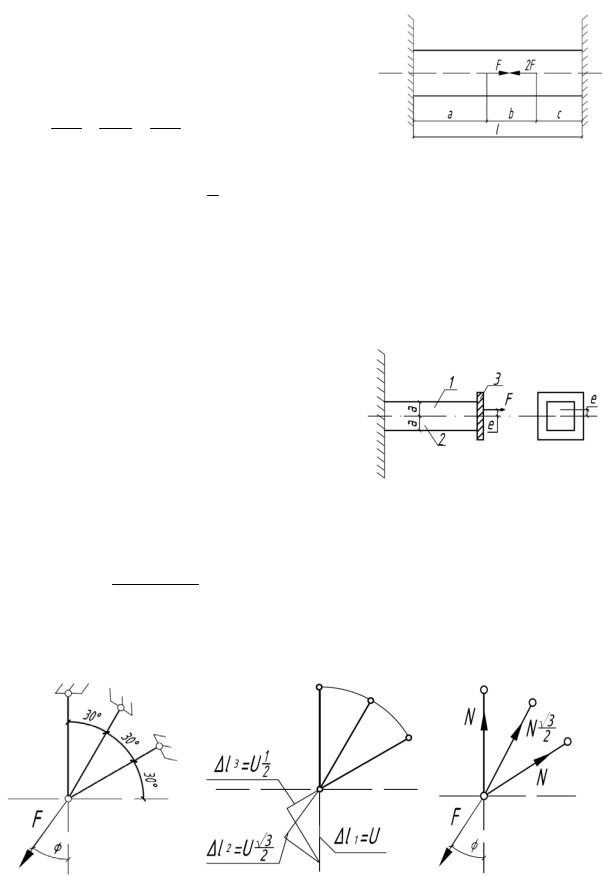
Р е ш е н и е
а) N1 RA, N2 RA по условию;
N 2RA F : RA F / 2;
N3 RB RA F 2F 3F / 2;
б) l NE1Aa NEA2b NEA3c 0 : a b 3c 0;
в)
b l a c : 2a 4c l, c 4l a2 ; a 0 : c l / 4.
Ответ: 0 c l / 4.
6.7. Квадратный стержень (2а 2а) состоит из двух половинок,
изготовленных из разных материалов (E1 > Е2). Считая концевую пластину 3 абсолютно жесткой, определить эксцентриситет приложения силы Р, при котором каждый стержень будет находиться в состоянии осевого растяжения.
Решение Положение нейтральной оси Х при изгибе:
Ei Ei 1 y, a e y a e ;
N dA dA dA 0 :
|
A |
A1 |
A2 |
|
|
|
|
|
|
|
|
|
|
1 |
E1S1, X |
E2S2, X 0, E1 2a |
2 |
a |
|
E2 2a |
2 |
a |
|
0. |
|||
|
|
|
2 |
e |
|
|
2 |
e |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: e a E1 E2 . 2 E1 E2
6.9. Под каким углом нужно приложить силу F к узлу, чтобы
его перемещение было направлено по вертикали? Материал стержней один и тот же.
Рис. 6.9 |
Рис. 6.9(а) |
Рис. 6.9(б) |
Решение
137
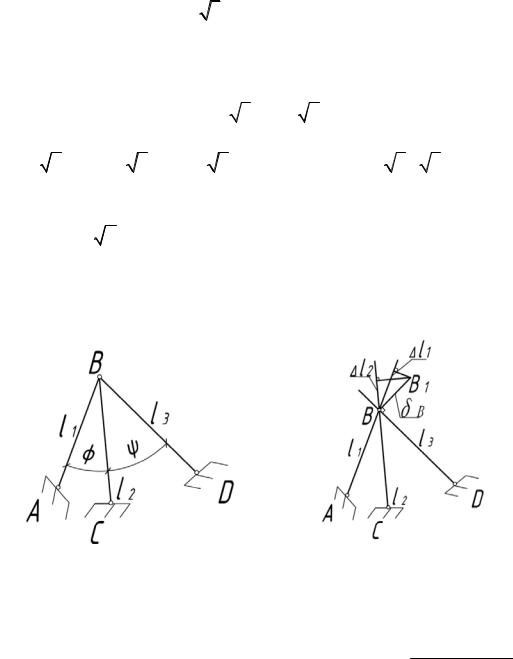
а) Статика. Из равновесия узла:
|
|
|
|
X 0 : F sin |
|
N2 sin 30 N3 sin 60 ; |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
Y 0 : F cos N1 N2 cos30 N3 cos 60 . |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
б) Геометрия. По условию, u y : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
l1 |
|
u, |
l2 |
u cos30 , |
|
l3 u cos60 ; |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
l |
|
l |
|
|
3 |
; |
|
|
|
l l |
1 . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
3 |
|
|
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|||||
в) Физика. l |
|
N1l |
|
N1l |
, |
|
l |
2 |
|
|
N2l |
|
N2l |
; |
l |
|
N3l |
|
|
|
N3l |
. |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
1 |
|
EA1 |
|
|
|
EA |
|
|
|
|
|
|
|
|
|
|
EA2 |
|
EA |
|
3 |
|
|
EA3 |
|
|
2EA |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Тогда, N |
|
N |
N; |
|
|
|
|
|
|
N |
|
N |
|
3 |
N |
3 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
3 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
F sin N |
3 |
1 |
N |
|
|
3 |
N |
|
|
3 |
3 |
|
; |
F cos N |
|
N |
|
3 |
|
3 |
|
N |
1 |
N 9 . |
|||||||||||||||||||||
2 |
|
|
2 |
|
|
|
|
4 |
|
|
|
|
|
2 |
2 |
|
|
||||||||||||||||||||||||||||
|
|
1 |
2 |
|
1 |
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
1 2 |
1 4 |
||||||||||||||||||
Ответ: tanφ |
|
, |
|
φ 30 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
6.10.Стержни АВ и ВСвыполнены из одного материала. Углы
φи заданы. Найти соотношение между длинами l1 и l2 , при
котором в стержнях фермы не возникают температурные усилия от нагревания стержней АВ и ВС на t .
Рис. 6.10 |
Рис. 6.10(а) |
|
|
|
|
|
|
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
|
|
N1 N2 |
N3 |
0, если l3 0, |
т.е. |
|||||||
l |
|
B |
cos |
|
|
|
B |
sin |
tl |
, |
|||||
1 |
|
|
|
|
|
|
|
|
|
t |
|
1 |
|
||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
l2 |
|
|
|
|
|
|
B sin t tl2 , |
|
|
|
||||
|
B cos |
2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: l1 / l2 sin φ ψ / sin ψ.
B l3.
l1 B sin ;t t
l2 B sin .
t t
138
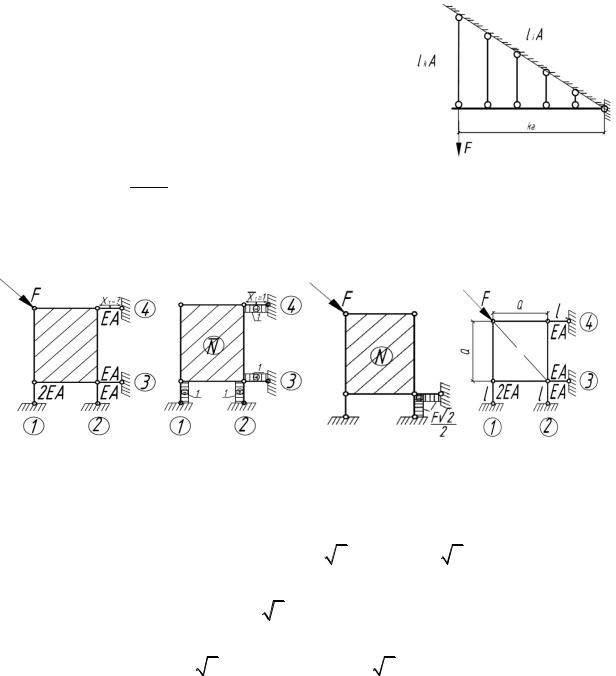
6.12. Абсолютно жесткий брус поддерживается k стержнями (k – произвольное число), изготовленными из одного материала и одинаковой площади ( l1 = а, l2 = 2а, lk = ka). Определить усилия
в стержнях.
Решение
|
li i a, |
|
i 1,2, , k; |
|||||||
l |
d ia d l |
|
|
Ni li |
: |
N |
i |
d EA N; |
||
|
|
|||||||||
i |
i |
|
|
EA |
|
|
|
|
||
|
F ka Ni ia |
|
Na i Na k k 1 . |
|||||||
|
k |
|
|
k |
|
|
|
|
|
|
|
1 |
|
1 |
|
|
2 |
|
|||
Ответ: Ni 2F . k 1
6.13. Определить усилия в стержнях, поддерживающих абсолютно жесткую плиту.
Решение
Система один раз статически неопределима: 11X1 1F 0.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 l |
|
12 l |
|
|
7l |
|
|
||||
11 |
N |
N |
|
ds |
|
3 |
|
|
; |
|
|||||||||||||||
|
|
EA |
|
|
EA |
2EA |
|
2EA |
|
||||||||||||||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
F |
2 l 1 |
|
|
|
Fl 2 |
|
|||||||||
1F |
|
N |
ds |
2 |
|
; |
|||||||||||||||||||
|
|
|
EA |
|
2 EA |
|
|
|
EA |
|
|||||||||||||||
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X1 |
1F |
2 2 |
F; |
|
|
|
X1 NF . |
|
|||||||||||||||||
|
N N |
|
|||||||||||||||||||||||
|
11 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Ответ: N1 N4 2 |
7 |
2 |
F; |
|
|
N2 N3 |
|
3 2 |
F. |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
||||
6.14. Абсолютно жесткая рама ABCD закреплена, как показано на рисунке. Определить усилия в стержнях 1 и 2 при действии на раму сосредоточенного момента M, если известно, что жесткости стержней одинаковы: Е1А1 = Е2А2= ЕА, а их длины l1 = а, l2 = с.
139
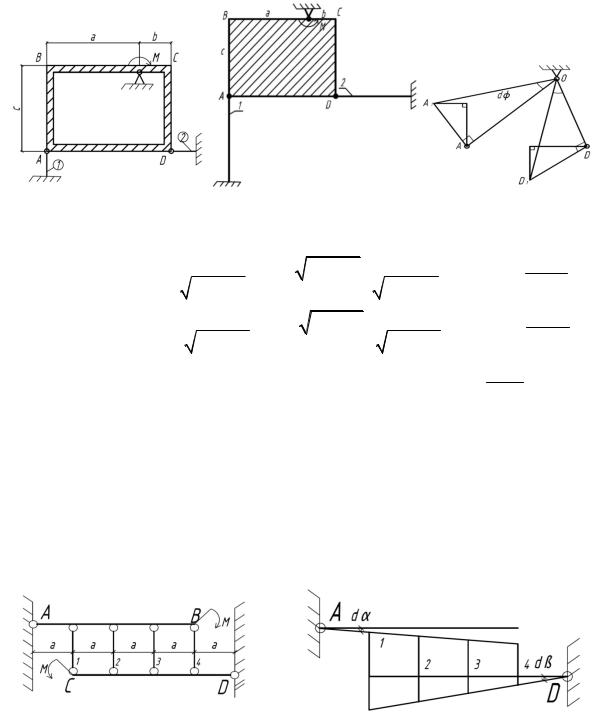
Рис. 6.14 |
Рис. 6.14(а) |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
Решение |
a |
|
||||
|
A |
l |
AM |
: |
l |
A |
|
|
|
|
|
|
d |
a2 c2 |
|
|
||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
1 |
|
|
|
|
a2 c2 |
|
|
|
|
|
a2 c2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
D |
l |
DM |
: |
l |
A |
|
|
c |
|
|
d |
b2 c2 |
c |
|
|||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
2 |
|
|
|
|
b2 c2 |
|
|
|
b2 c2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
M 0: |
M N1 a N2 c; |
N1 N2 N : |
|
||||||||||||||
Ответ: |
N1 N2 |
|
|
|
M |
. |
|
|
|
|
|
|
|
|||||||
|
a c |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
d a N1 a ;
E1A1
d c N2 c .
E2 A2
N aM c .
6.15. Стержневая система состоит из двух параллельных абсолютно жестких балок АВ и CD, соединенных четырьмя упругими вертикальными стержнями, имеющими одинаковые жесткости на растяжение. Определить усилия в стержнях, возникающие после приложения к балкам в точках В и С одинаковых по величине моментов М.
Рис. 6.15 Рис. 6.15(а)
Решение
Статика.
M 0 : |
N1 1 N2 2 N3 3 N4 4 M / a; |
A |
|
M 0 : |
N1 4 N2 3 N3 2 N4 1 M / a. |
D |
N1 N2 N3 N4 0; |
|
|
|
140 |
