Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2381

.pdf

Скачиваний:

Добавлен:

17.06.2024

Размер:

8.13 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1713 14 15 16 17 > Следующая >>>

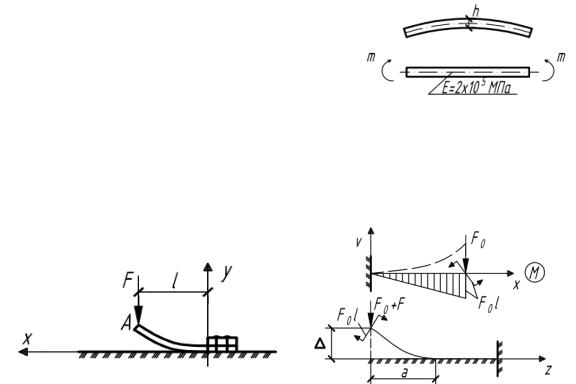
5.44. Стальная полоса изготовлена с начальной постоянной кривизной. Каким должен быть радиус кривизны, чтобы после выпрямления

σmax = 200 МПа?

Решение

max

, M max I

;

max

200 МПа

500h.

200 ГПа

Ответ: ρ 500h.

5.45. Плоскаястальнаяпружинаоднимконцомпривинченакстолу. Предварительно пружина изогнута по кривой у = kx3. К пружине прикладывается сила F. Найти b – длину контакта пружины со столом и величину перемещения точки А (рис.5.45).

Рис. 5.45

Рис. 5.45(а)

Решение

а) 0 x l,

x kx

M x

6kx,

Q x

A 6kl,

F0,A

6k;

б) z l x,

0 z a;

0 ,

M A EI 6kl,

FA F EI 6k;

EI z EI EI

z M

;

EI a 0:

0 EI EI a M

a2 F

a3 ;

FAa3

;

6EI

;

EI 0 FA

;

EI a 0:

EI 0 M Aa FA

a M A

EI6kl

EI a 0:

0 M

F a;

F EI6k

Ответ: b l a

;

A kl3

k l3 a3

Fa3 .

EI6k

6EI

121

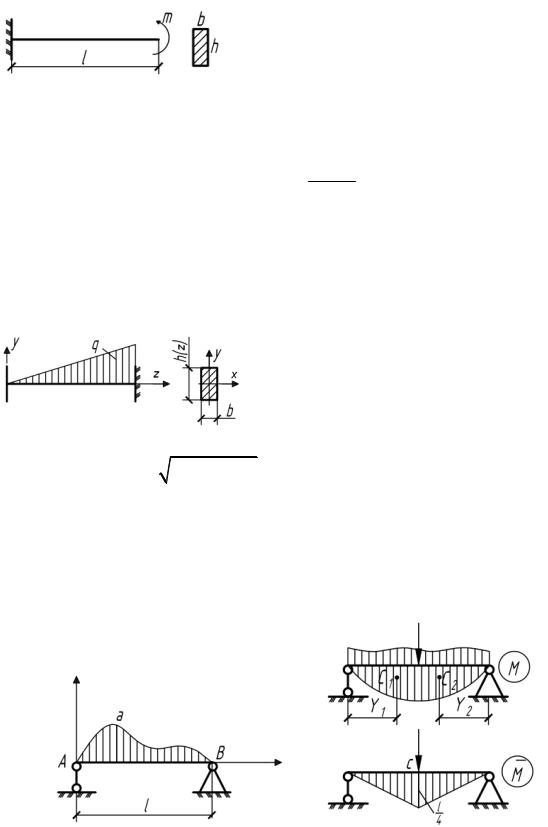
5.46. Как при одном и том же прогибе на конце балки изменится

прочность балки постоянного сечения, если ее высоту увеличить в два раза?

Решение

M l2

1,maxl2

1 ,

;

1,max

2EI1

2 h,

2,maxl2

, 2,max

;

2EI2

1 2 : 1,max 2 2,max .

Ответ: прочность уменьшится в 2,max 2 раза.

1,max

5.47. Консольная балка длиной l загружена распределенной по линейному закону нагрузкой. Поперечное сечение балки прямоугольное с

постоянной шириной b и переменной по длине высотой h z . Уста-

новить закон изменения высоты сечения по длине балки, если продольная ось изогнулась по дуге окружности радиусом .

Решение

0 z l :

M x z qz

;

Ix z bh3 .

M x z

const,

2qz3

EIx z

Elbh3

Ответ: h h z z 3 2qρ / Ebl .

5.48. Определить прогиб в середине пролета балки, имеющей постоянную изгибную жесткость сечения EI и длину l, если известно, что статический момент части площади эпюры изгибающего момента, лежащей слева отсреднего сечения, относительно вертикальнойоси, проходящей через опору A, равен S1 , а статический момент остальной пло-

щади эпюры относительно оси, проходящей через точку В, равен S2 .

Рис. 5.48

Рис. 5.48(а)

122

Решение

S1 Ω1 Y1;

S2 Ω2 Y2

M M

C EI

Ω2

2EI

EI Ω1

Ответ: C S1 S2 .

2EI

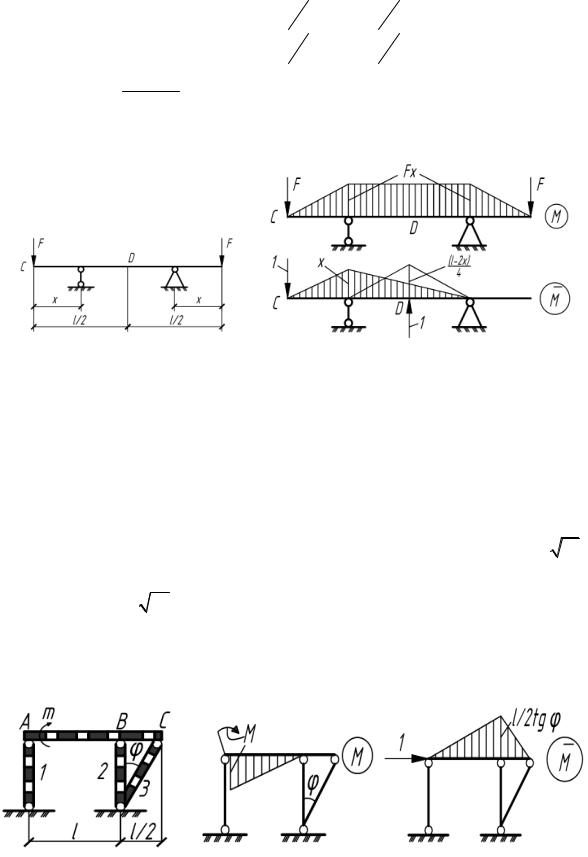
5.49. При какой длине консоли x прогибы балки в точках С и D одинаковы по абсолютной величине? (рис.5.49).

	Рис. 5.49																			Рис. 5.49(а)
										Решение
														Fx3			l 2x Fx2
					M M				C dz			1		Fx3									;
									C dz														;
				C		EI						EI				3			2
						EI						EI				3			2
					M							1				l 2x 2
					M		M			D		1				l 2x 2
				D						D	dz									Fx	;
				D			EI				dz						8			Fx	;
							EI						EI				8

	x2		x l 2x					l 2x 2							x 2			6	x			3		x	6	15
C D :												,											0,				.
C D :	3			2						8		,						7				28	0,	l	14		.
	3			2						8					l			7	l			28		l	14
Ответ: x		6		15 l 0,152l.
			14

5.50. Стержень ABC с постоянной жесткостью EI шарнирно закреплен на абсолютно жестких стержнях 1, 2, 3. Определить горизонтальное перемещение стержня ABC при действии момента M.

Рис. 5.50

Рис. 5.50(а)

123

Решение

M M

2 tan

Ответ: X

Ml2

влево.

12EI tanφ

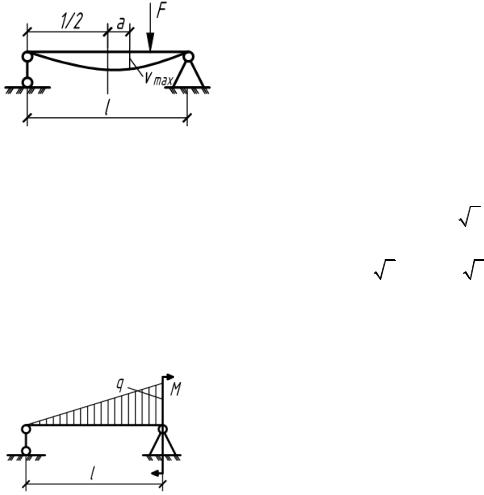
5.52. На балку действует сосредоточенная сила F. Определить величину amax – наибольшего удаления сечения с максимальным

прогибом от середины балки. Какому

нагружению это соответствует?

Решение

Нагружение: F на расстоянии dz от опоры

В, т.е. от M = F dz;

F dz

M .

EI z EI 0 z RA

, l 0 : EI 0 RA l2

;

EI z RA l2 RA

z 0 :

;

z max , когда

z 0 :

Ответ: amax 0,07735l

от M

на левой опоре.

5.53. Дано: q, l. Найти значение момента M , при котором максимальный прогиб будет в среднем сечении.

													Решение
								0; Q					R		A		ql					1 M ;								q		0.
									0			0			A				2			3					l			0
																			2			3					l
										EI z			EI 0 z RA											z3		q			z5		;
										EI z			EI 0 z RA													q					;
																						6					l	120
							l 0 :				EI 0 RA l2												ql3						Ml				7ql3	;
							l 0 :				EI 0 RA l2																	6					360	;
																			6			120						6					360
					EI z EI 0 RA								z2	q						z4	;
					EI z EI 0 RA								2	q							;
													2			l			24
				l											l
						max ,				когда										0 :
						max ,				когда						2				0 :
				2												2
	Ml			7ql3			ql			M l2			ql3									M				7ql		2
0																		,												.
0		6		24 15				6			8		24 16					,							15 16					.
		6		24 15				6		l	8		24 16												15 16
Ответ: M		7ql2
Ответ: M		240	.
		240

124

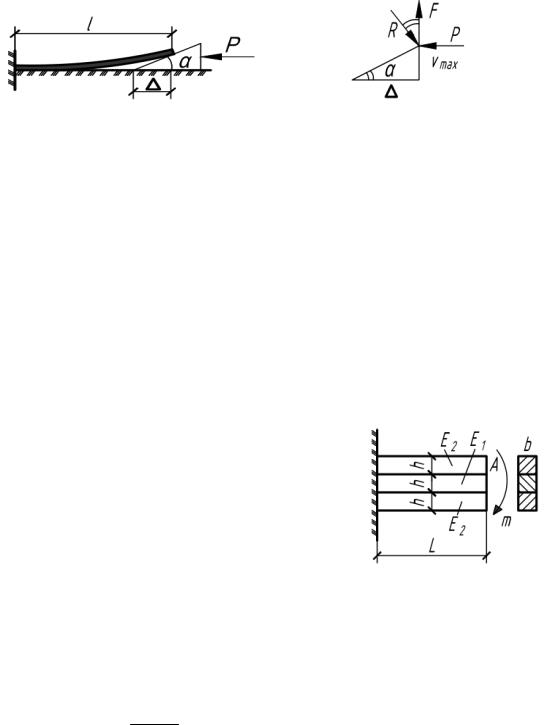
5.54. Клин с малым углом перемещается под действием силы P на

величину ∆, поднимая конец балки. Не учитывая силы трения, установить зависимость P = f( ) при условии, что угол поворота концевого сечения балки не превышает (рис.5.54).

Рис. 5.54

Рис. 5.54(а)

Решение

Из равновесия: X 0 :

Rsin P;

Y 0 :

F Rcos ;

tan

Fl3

3EI tan2

max

;

max

tan ;

3EI

Ответ: P

3EI tan2 α

5.55. Поперечное сечение консольной балки, загруженной на конце

моментом M иизготовленнойиз двух материалов, показано нарисунке.

Найти прогиб в точке А,

если модуль упругости E2 2E1 . Проскаль-

зывание между брусками исключено.

Решение

Нейтральная ось X ось симметрии сечения.

E E

;

I bh3

;

I bh h2

13I ;

EIпр E1I1 2E2I2 53E1I1;

M x dA y

EIпр

;

E1 y dA 2 E2 y dA

Ml2

12Ml2

0,1132

Ml2

2EI

106E I

106E bh3

E bh3

max

пр

1 1

Ответ: max 0,1132 Ml23 .

E1bh

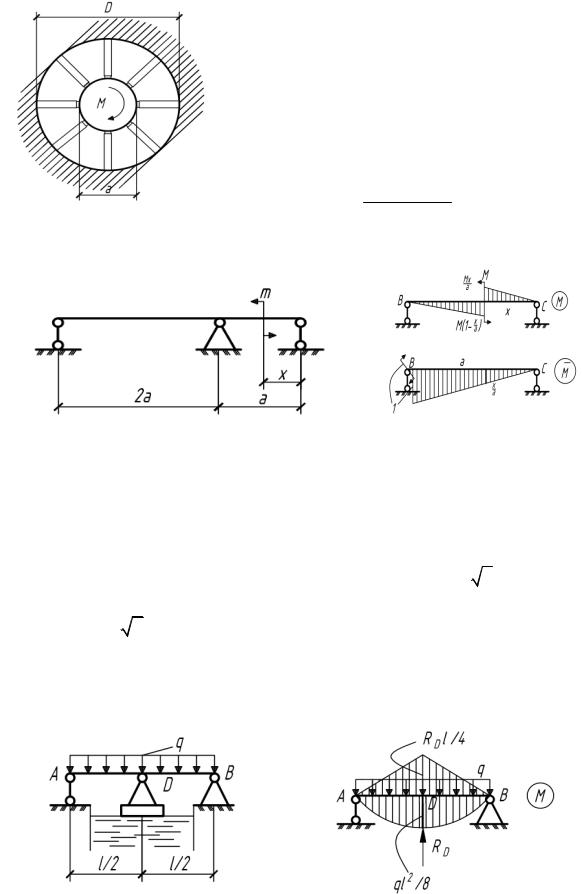
5.56. К абсолютно жесткому диску диаметром а шарнирно прикреплены спицы – круглые стержни диаметром d, второй конец которых жестко защемлен. Определить угол поворота диска от действия момента М в плоскости этого диска.

125

Решение

8F a

;

Fl3

d 4

D a

;

3EIx

D a 3

M D a 3

3E d

E a

Ответ: θ 4 M D 2 a4 3 .

3 Eπa d

5.57. При каком расстоянии x на левом пролете балки отсутствуют прогибы? (рис.5.57).

Рис. 5.57

Решение

Рис. 5.57(а)

если

A B C 0;

AB 0,

B 0;

1 a x

M M

;

0 :

2 1 3 0,

Ответ: x

0,57735a.

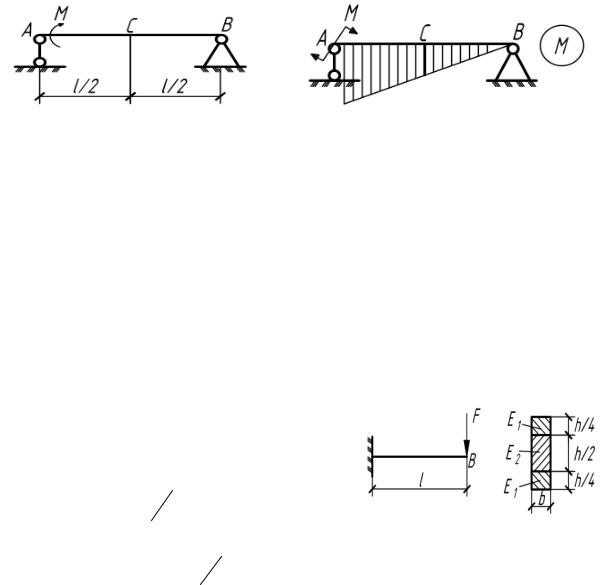
5.59. Мост через реку, несущей конструкцией которого

является балка АВ, усилен с помощью понтона D. Определить А – площадь понтона в плане, при которой воспринимаемая им нагрузка составит 25% от полной нагрузки моста (рис.5.59).

Рис. 5.59

Рис. 5.59(а)

126

Решение

по условию ;

A 0,

B 0;

RD 0,25ql

5ql4

R l3

ql4

M M

D EI

dz q RD

;

384EI

48EI

128EI

32EI .

32EI

Ответ: A

γl3

5.60. Требуется экспериментально определить угол поворота сечения С. Однако конструкция установки позволяет замерять углы поворота только на опорах. Как определить искомый угол φc при заданной нагрузке? (рис.5.60).

Рис. 5.60

Рис. 5.60(а)

Решение

M A

;

M B

A ;

3EI

6EI

M MC dz

B .

24EI

Ответ: φC φA

φB .

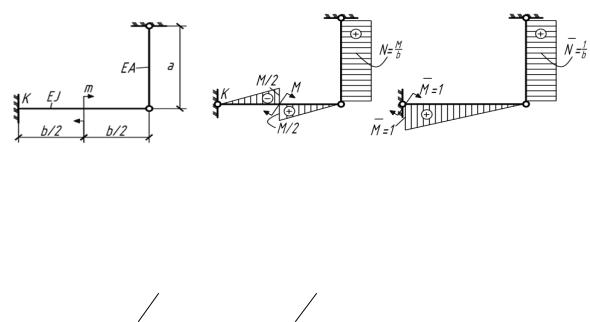
5.61. Определить прогиб B в балке, выполненной из разномодульных материалов. Дано: F, l, h, b, E1 , E2 .

Решение Нейтральная ось X ось симметрии

сечения.

E E		1 y,	h	y h	;
i	i		2	2


I2	b h 2 3			bh3	;
I2	12			96	;
	12			96
	I	b h 4 3			bh	3h 2	7bh3	7 I		;
	I				bh		7bh3	7 I	2	;
	1		12		4	8	192	2	2
			12		4	8	192	2

127

					EI			2E I E I										E I					7	E1		1 ;
					EI		пр	2E I E I									2	E I			2		7			1 ;
							пр				1 1				2		2			2	2			E2
																								E2
												1						2					2						EIпр
		M x dA y													E2 y dA 2 E1 y dA																;


				A										A2								A1
	B			max			Fl3										Fl3										32Fl3						.
							3EI			пр			3E I						E						E bh		3			E			.

																		7			1							7				1
																			1											1
																			E											E
															2	2			E				2							E
						32Fl3													2											2
Ответ: B						32Fl3									.
Ответ: B			E2bh			3			E						.
						3			E
							7			1	1
							7		E2		1
									E2

5.63. При каком значении а изгибающий момент в поперечном сечении К балки равен нулю? (рис.5.63).

Рис. 5.63

Рис. 5.63(а)

Решение

K 0, K 0; MK 0 по условию, т.е. как в шарнире рис.5.63 а .


						K		M M			ds				N N				ds
						K					ds								ds
									EI							EA
	1		b	2		M		1				b		2	M			1			1		M	1
				2			2		1					2								a	b	b	;
			6			2	2	2	1				3		2			2				a			;
	EI		6			2		2					3		2			2			EA

						K 0 :				1				b			1		a	.
						K 0 :				EI			24							.
		A	b3							EI			24			EA			b2
Ответ: a		A	b3		.
Ответ: a		I	24		.
		I	24

5.64. В разрез тонкого кольца, радиус средней линии которого равен R, помещен небольшой брусок толщиной . Опре-

делить наибольший изгибающий момент, возникающий в кольце (рис.5.64).

128

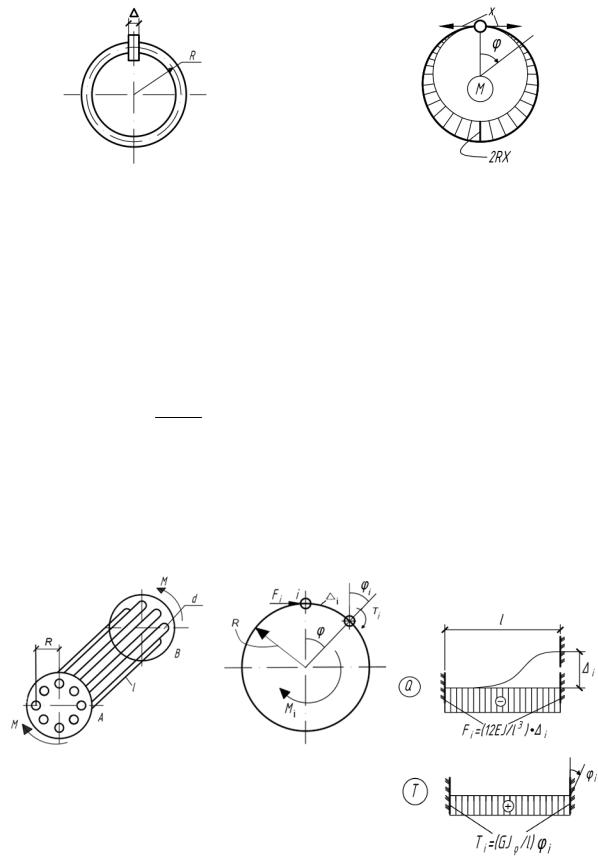
Рис. 5.64 Рис. 5.64(а)

Решение

0 2 ,

ds Rd ;

M X 1 cos R, Mmax M 2XR;

X 1 cos

2XR

sin 2

ds 2

2sin

;

C :

2 XR3

2 XR

2EI

3 R2

Ответ: Mmax 23EIπR2 .

5.65. В двух плоских параллельных дисках А и В жестко заделаны симметрично расположенные относительно продольной оси п круглых стержней диаметром d и длиной l. Считая диски абсолютно жесткими и упругие постоянные материала стержней известными, определить взаимный угол поворота дисков при нагружении системы двумя скручивающими моментами М (рис.5.65).

Рис 5.65

Рис. 5.65(а)

129

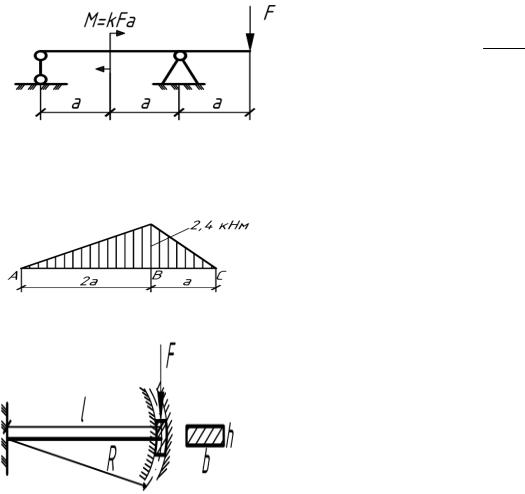
Решение

i 1,2, ,n :

M M

T ;

2I I

d 4

;

i,и

2 1

i,и

F R

12EI

12EIR2

; T

;

12EIR2

;

Ответ:

Ml3

32Ml

12EIR2 GI

R 2

nEπd 4

Задачи для самостоятельного решения

5.1. При каком значении коэффициента К прогиб конца консоли равен нулю? Чему при этом равен угол поворота этого же сечения?

Ответ: k 12; φc 6FaI2 .

E x

5.5. По заданной эпюре изгибающего момента определить угол поворота сечения С балки, если прогибы в сечениях А и В равны нулю,

EI = 200 кН м2, а=1 м. (рис.5.5).

Ответ: 0,014 рад по часовой

стрелке.

5.10. Один конец стальной балки (b = 60 мм, h = 20 мм) жестко защемлен, а другой жестко заделан в ползун, движущийся по окружности радиуса R = l. Определить σmax в балке, а также

прогиб и угол поворота концевого сече-

ния, если F = 1,5 кН, R = 0,5 м, E=200 ГПа.

Ответ: σmax 125 МПа;

B 3,9 мм; φB 0,0078 рад.

130

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 1713 14 15 16 17 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.06.20248.07 Mб02377.pdf
#
17.06.20248.08 Mб02378.pdf
#
17.06.20248.08 Mб02379.pdf
#
17.06.2024243.89 Кб0238.pdf
#
17.06.20248.09 Mб02380.pdf
#
17.06.20248.13 Mб62381.pdf
#
17.06.20248.16 Mб02382.pdf
#
17.06.20248.23 Mб02383.pdf
#
17.06.20248.23 Mб02384.pdf
#
17.06.20248.23 Mб42385.pdf
#
17.06.20248.24 Mб02386.pdf