Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2381

.pdf

Скачиваний:

Добавлен:

17.06.2024

Размер:

8.13 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1712 13 14 15 16 17 > Следующая >>>

		1		3l		4										3l							Fl					3l					3l		4					3l							3l				1					F									X			3l 3
						4				2 Fl																									4	X																																					;
	EI									2 Fl						4							4											3		X					4						4				EI						2							3									;
	EI				6											4							4						4					3							4						4				EI						2							3					4

																					1			3l								3l			3l								1						X 3l 3
2,B							MM														1			3l			4					3l			3l								1						X 3l 3
													dz														4			X																													;
								EI					dz						EI											X		4			4							EI																	;
								EI		2									EI						3							4			4							EI							3 4
										2
					2,B		:		X 3 F;
1,B					2,B										4
		1 F,													4			7																																		7						z2					1 F				z3
R									M		1, A							7				Fl,															EI								z							7			Fl			z2									z3			;
R									M													Fl,															EI								z										Fl															;
1, A				4													16																						1				1								16								2					4		6
				4													16																																		16								2					4		6
R			3 F,						M			2, A								9			Fl,														EI				2					2	z							9		Fl					z2				3 F				z3		;
R			3 F,						M														Fl,														EI										z									Fl									3 F						;
2, A				4													16																																				16									2				4		6
				4													16														z2							z3															16									2				4		6				z2
									,				EI z												2					Fl	z2			1 F				z3						;					EI d											2				Flz 1 F								z2		;
									,				EI z																	Fl				1 F										;					EI d															Flz 1 F										;
				1				2																16								2			2				6													dz							16							2							2
																								16								2			2				6													dz							16							2							2
d													l																			l				1												3		1			1						1					1						Fl3
			0 :					z						,				max																									Fl																																.
dz			0 :					z				2		,				max																			EI						Fl							16			4				12											192EI							.
dz												2																				2					EI													16			4				12							8				192EI
	Ответ:							max												Fl3						.
	Ответ:							max								192EI										.
																192EI

5.27. Определить модуль упругости материала балки, радиус кривизны оси балки в сечении А и угол поворота на свободном конце,если σmax = 70 МПа и прогиб в точке В равен 2 см (рис.5.27).

Рис. 5.27

Решение

ql4

ql2

max

;

8EI

max

70 МПа

4 м2

70 ГПа;

2 см

20 см

70 ГПа

5 см 50 м;

Mmax

max

70 МПа

ql3

2 см 4

0,013 рад.

6EI

3 2 м

Ответ: E 70 ГПа;

ρA 50м;

φB 0,013рад по .

111

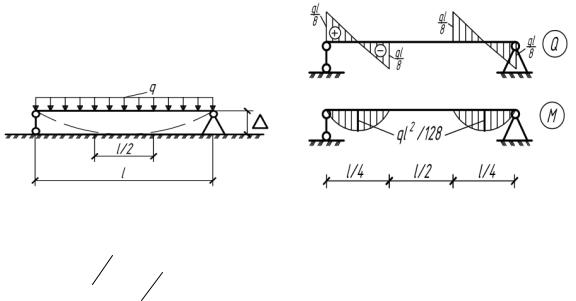
5.28. Длинный гибкий стержень жесткостью EI лежит на жестком основании и поднимается за середину силой F. Полагая погонный вес стержня q, определить длину а оторвавшейся от основания части. Построить эпюру Q и M (рис.5.28).

Рис. 5.28

Рис. 5.28(а)

Решение

0 z a 2 : 0 0, Q0 F 2, q0 q;

Универсальное уравнение изогнутой оси балки:

				EI z EI EI												z M					z2			Q					z3			q				z4
				EI z EI EI												z M						2		Q					6			q
												0		0					0			2					0		6					0 24
									EI M									z2		F z3						q			z4			;
									EI M									2		2			6			q			24			;
													0		0			2		2			6						24
																															2							a		3				a	4
a				0			EI a						0:				0 EI M												a				F					a			q			a			;
a				0			EI a						0:				0 EI M										0		a				F								q						;
		2																				0					0			8				2			48						384
		2								2																				8				2			48						384
	a									a																				a				F			a2					a3
				0				EI					0:				0									M0															q				;
		2		0				EI					0:				0									M0				2				2			8				q	48			;
		2								2																				2				2			8					48
		a							¨		a							0								M0									F				a		q	a2			;
M			0						EI			0:						0								M0									2				2		q	8			;
		2									2																								2				2			8

a		3		F			M				F	a q		a2						15					F 2					EI										675				F 4
						;		0																				;																		.
						;																						;																		.
		2		q							2			8						32						q								0					6144					q3
		2		q							2			8						32						q													6144					q3
Ответ: a					3		F .
					2		q

112

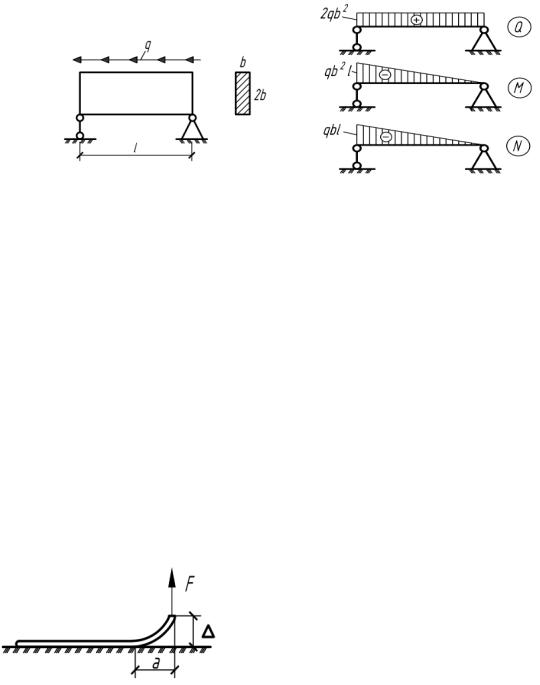
5.29. Определить, при какой нагрузке q балка жесткостью EI, опирающаясянаопорывысотой , будетиметьсплошноекасаниенадлине l/2 с абсолютно жесткой плитой. Построить эпюры Q, М по длине балки

(рис.5.29).

Рис. 5.29 Рис. 5.29(а)

l l

Решение

, 0 z a :

M 0; Q R , q q;

Универсальное уравнение изогнутой оси балки:

EI z EI

z M

EI EI

z R

;

0 2

A 6

0 6

0 24

EI a 0:

0 EI EI a R

;

EI 0 RA

EI a

;

M a 0

a q a

EI a 0:

;

EI 0

qa3

ql3

;

24 EI

6144 EI

768

Ответ: q

6144 EI

113

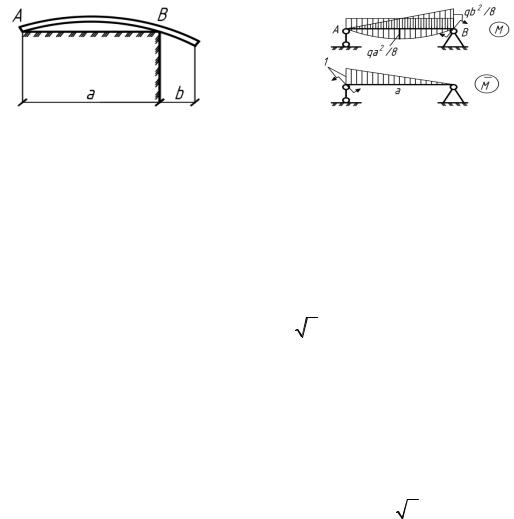
5.30. Определить угол поворота сечения над левой опорой балки.

Дано: q – равномерно распределенная по поверхности, b, l, E(рис.5.30).

Рис. 5.30 Рис. 5.30(а)

Решение

m qb b qb2;

Q RA qbl 2b

2qb2;

Q m qb2;

qbl;

H b qb2l;

b 2b 3

2b4

;

ql2

A dz

EIx

2Eb

ql2

EIx 3

Ответ: φA

2Eb2

5.31. На абсолютно жестком основании лежит полоса прямоугольного сечения b h с погонным весом q. Определить, на какой длине а

полоса приподнимется над плоскостью при приложении к ее концу силы F а также перемещение .

Решение

0 z a : 0 , M0 0; Q0 F, q0 q;

Универсальное уравнение изогнутой оси балки:


EI z EI EI		z M		z2			Q			z3	q	z4
EI z EI EI		z M			2		Q		6		q
0	0		0		2		0		6		0 24
EI EI 0 z F						z3		q	z4		;
EI EI 0 z F					6			q	24		;
					6				24

114

Fa q a2 ; 2

q a3 ; 6

EI 0 F a2

a 0, EI a 0: 0 EI EI 0a F 6

a 0, EI a 0: 0

M a 0, EI ¨ a 0: 0

Ответ: a	2F	;	8F 4	.
	q		q3 Ebh3

q	a4	;	Fa3	8F4	;
	24		12EI	q3Ebh3

EI 0 qa3 ; 12

a 2qF ;

5.32. Гибкий весомый стержень (погонный вес q) лежит на абсолютно жесткой плоскости. При каком минимальном соотношении b/а стержень касается плоскости лишь в двух точках –А и В? Определить возникающие опорные реакции (рис.5.32).

Рис. 5.32 Рис. 5.32(а)

Решение

A 0,

RA 0,

M A 0;

R 0, M

qb2

b a;

;

															2					2					3			2
			M M dz							1		a qb 1 2 a qa 1											qa			b		2	1
										1																b			1	;
	A																													;
	A			EIx								6 2					3		8 2										2
				EIx					EIx			6 2					3		8 2					12		a			2
												A 0 :					b		2	.
												A 0 :					a			.
																	a		2
							RA				qa			qb2		1		qa			b	2		;
							RA				2			2		a		2	1					;
											2			2		a		2			a

							R				qa			qb2		1		qa			b	2		;
							R												1					;
							B				2			2		a		2
											2			2		a		2			a

Ответ:		R			qa	1		b 2					;	R			qa		1	b 2			;		2		b	1.
								a												a							a
					2												2							2
			A		2										B		2							2

115

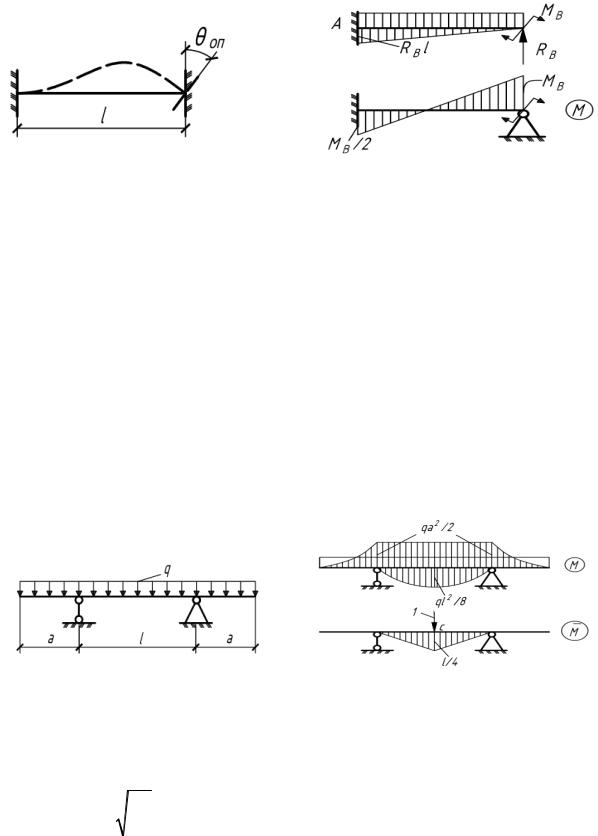
5.33. Правая заделка балки постоянной жесткости повернулась на угол θоп . Найти угол поворота поперечного сечения, в котором кри-

визна оси балки равна нулю (рис.5.33).

Рис. 5.33

Решение

Рис. 5.33(а)

RA RB ;

A 0,

B 0,

B оп;

EI z M A

;

EI z M A z RA

;

M z M A RA z;

l 0 :

0 M A l2

RA l3

, RA

3M A ;

M l M B :

M A M B ;

M l R

M l

;

оп

M l

0 :

; EI

M A

оп .

2 3

оп .

Ответ: φ

5.34. На балку действует равномерно распределенная нагрузка q. При каком соотношении а/l прогиб в середине балки будет равен нулю?

Рис. 5.34

Решение

Рис. 5.34(а)

qa2

2 ql2 5 1l

ql2

5l2

M M

;

EIx

2 3 8 8 4 2 4

EIx 16

EIx

C 0 :

Ответ: a

0,4564.

116

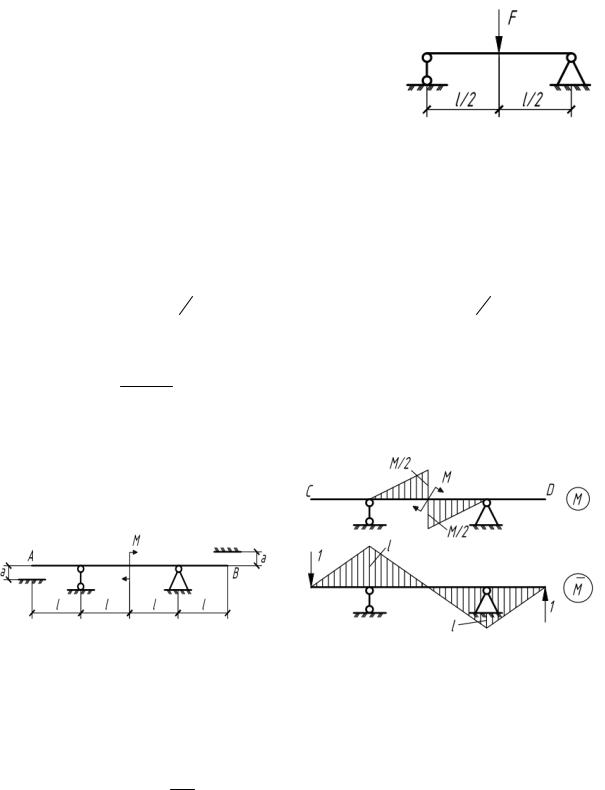
5.36.Определить площадь Ω, заключенную между первоначальной

иизогнутой осью балки. F, l, EI заданы

(рис.5.36).

Решение

A B 0,

A B ;

Из симметрии: R

;

Рис. 5.36

EI z EI 0 z

;

EI z EI 0

;

Fl2

EI 0

0 :

;

Fl2

Fz3

5Fl4

z dz

2EI

384EI

Ответ: Ω 5Fl4 .

384EI

5.37. Принимаяа= l/1000, установить, прикакомзначенииМконцы балки будут касаться опор А и В (рис.5.37).

Рис. 5.37

Рис. 5.37(а)CD-AB

Решение

Ml2

12EI

M M

EIx

2a :

EIx

Ответ: M 0,012 ElI .

117

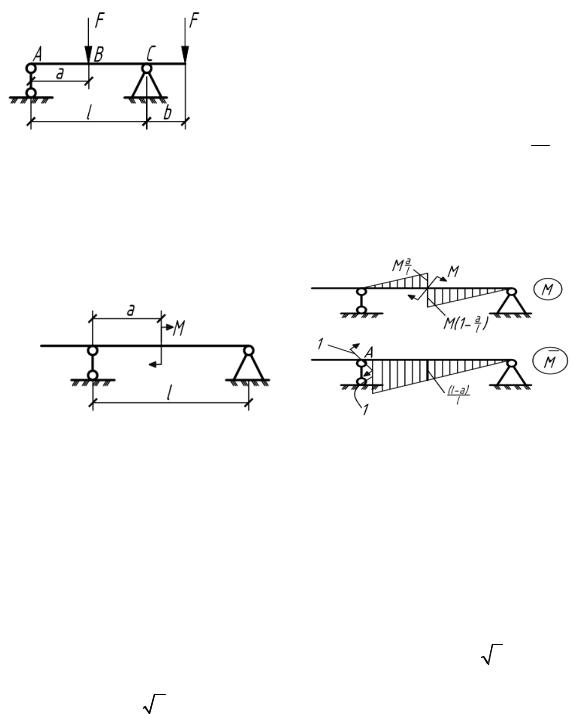
5.38. Подобрать размер а таким образом, чтобы прогиб балки на участке АВ изменялся по линейному закону.

Решение

A 0;	M A 0;
MC 0 : RA		F l a Fb	;
MC 0 : RA		l	;
		l

0 z a, EI z EI 0 z RA z63 :

RA 0, l a b.

Ответ: a l b.

5.39. На каком расстоянии а нужно приложить внешний момент М, чтобы консольный участок балки остался горизонтальным? (рис.5.39).

				Рис. 5.39																			Рис. 5.39(а)
													Решение
	M								1	l a				M		l a			l a			a		Ma	l a				1 a
	M		M		dz				1	l a				M		l a			l a			a		Ma	l a				1 a
A																														;
A		EIx									3					l			l			2		l		l				;
		EIx						EIx			3					l			l			2		l		l			3 l
a		1;
l							3
			1				3		2			2					2			2							1
												2					2			2							1
A 0 :					3				2	1		3			,			2		3	0,			1				0,423.
A 0 :										1					,			2			0,			1			3	0,423.
						1																					3
Ответ: ξ 1						1		0,423.
Ответ: ξ 1							3	0,423.
							3

5.40. Под действием двух сил F первоначально искривленная пластинка выпрямляется и плотно соприкасается с плоскостью. По какой кривой должна быть искривлена пластинка, чтобы после выпрямления давление по длине l распределялось равномерно? (рис.5.40).

118

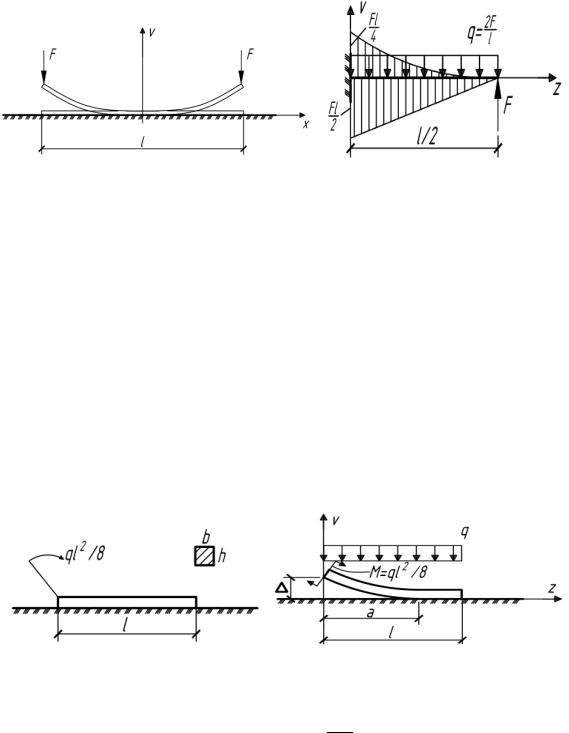
Рис. 5.40 Рис. 5.40(а)

Решение

Обратная задача:

0 z

, 0, 0, M

Fl , Q 0, q 2F .

EI z EI EI

z M

;

0 2

0 24

0 6

4 2

EI z

Fl3

z 2

z 4

Ответ:

;

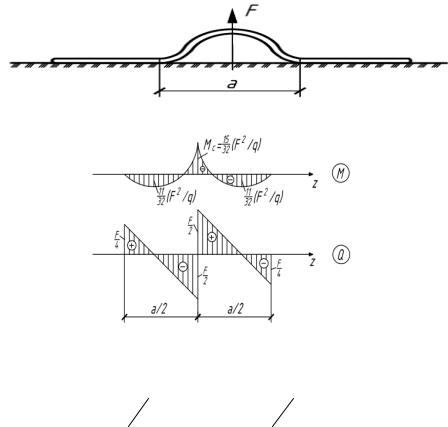
5.41. Балка длиной l и весом G=ql лежит на жесткой плоскости. Определить длину приподнятой части балки и величину наибольших нормальных напряжений при приложении к концу балки момента ql2/8. (рис.5.41).

Рис. 5.41 Рис. 5.41(а)

Решение

0 z a, 0 , 0 0, M0 ql82 , Q0 0, q0 q.


EI z EI EI		z M		z2		Q		z3	q	z4
				2				6
0	0		0				0		0 24
EI EI 0 z M0					z2		q	z4	;
					2			24

119

EI a 0:

Ответ: a 2l ;

0 EI EI a M								a2	q		a4		;					ql4			;
0 EI EI a M								2	q		24		;				128EI				;
				0			0	2			24						128EI
0			EI M					a q		a3		;			EI			ql3		;
					0		0			6					0			24
										6								24
0 M0 q			a2		;									a	2M	0			l	;
0 M0 q			2		;									a	q	0			2	;
			2												q				2
σmax	M	0	3		ql2	.
σmax		0	4		bh2	.
	Wx		4		bh2

5.42. По какой кривой следует первоначально изогнуть балку, чтобы при любом положении силы F на балке точка приложения силы после деформации оставалась бы на одном уровне?

Решение
Обратная задача: F F;				0 z l :
0 0, 0 0, M 0 Fz, Q0 F, q0 0;
EI z Fz	z2	F	z3	F	z3	.

2		6		3

Ответ: z Fz3 .

3EI

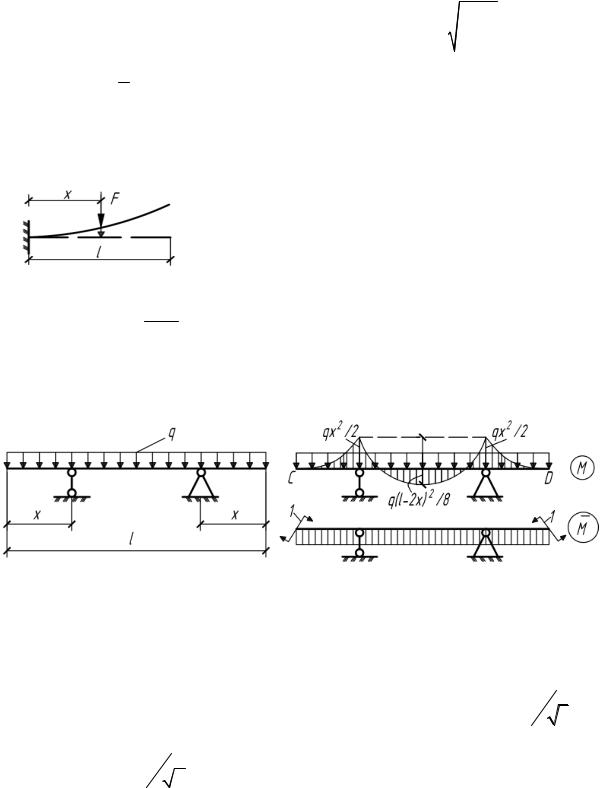
5.43. Двухконсольная балка постоянного сечения загружена как показано на рисунке. При каком расположении опор (х = ?) длина верхнеговолокнапризагружениинеизменяется, т.е. равнаl ? (рис.5.43).

Рис. 5.43	Рис. 5.43(а)
	Решение

				dz		1		qx2	2		x		1	q l 2x 2		2 l	2x		1 ;
	M M					1					x	l 2x		q l 2x 2		2 l	2x
	EI											l 2x
CD						EI 2				3			8				3
						EI 2				3			8				3
																		1
															x	1		1
	0 :		2x2 3l 4x l 2x 3									, 6x2 6xl l2 0,			x			3
	0 :		2x2 3l 4x l 2x 3									, 6x2 6xl l2 0,
CD															l			2
					1										l			2
Ответ: x		1			1	3	l 0,2113l.
						3
					2
					2

120

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1712 13 14 15 16 17 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.06.20248.07 Mб02377.pdf
#
17.06.20248.08 Mб02378.pdf
#
17.06.20248.08 Mб02379.pdf
#
17.06.2024243.89 Кб0238.pdf
#
17.06.20248.09 Mб02380.pdf
#
17.06.20248.13 Mб62381.pdf
#
17.06.20248.16 Mб02382.pdf
#
17.06.20248.23 Mб02383.pdf
#
17.06.20248.23 Mб02384.pdf
#
17.06.20248.23 Mб42385.pdf
#
17.06.20248.24 Mб02386.pdf