Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2381

.pdf

Скачиваний:

Добавлен:

17.06.2024

Размер:

8.13 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1711 12 13 14 15 16 17 > Следующая >>>

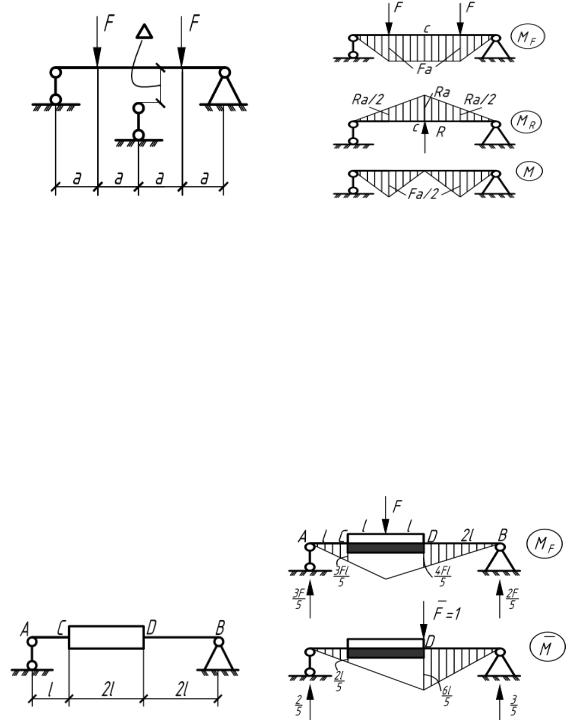
max	M0			Fl		6		480 Н 1 м						6			120 МПа.

	W			4		bh2				4			6	12		см3

Ответ: EIy x		Fl	3		Fx		2		l		x	x	2		σmax 120 МПа.
														;
		16				4				3		12l
								2

5.4. При каком значении осадки средней опоры изгибающий момент в сечении балки над этой опорой равен нулю? (рис.5.4).

Рис. 5.4

Рис. 5.4(а)

Решение

M M F M R :

M c 0,

Ra Fa,

R F.

Fa3

, где MR от

R 1.

2EI

Ответ:

Fa3

вниз.

2EI

5.6. Абсолютно жесткий однородный брус CD весом F жестко соединен с деформируемыми невесомыми стержнями АС и BD, изгибная жесткость которых равна EI. Определить вертикальное перемещение точки D (рис.5.6).

Рис. 5.6

Рис. 5.6(а)

101

						Решение						Fl3
					1 l		3Fl	2l	2l	4Fl	6l		18
D	M M		dz		1 l		3Fl	2l	2l	4Fl	6l		18	.
	EI											EI
						3	5	5	3	5	5		25
					EI	3	5	5	3	5	5		25
Ответ: δD	Fl3	18		.
Ответ: δD	EI	25		.
	EI	25

5.7. Стальная балка равного сопротивления изгибу пролетом l = 4 м имеет прямоугольное сечение с постоянной высотой h = 20 см. Интенсивность нагрузки q = 200 кН/м. Принимая R = 200 МПа, Е = 200 ГПа, найти наибольшую ширину bmax , а также наибольший прогиб max .

а) 0 z l,

Решение:

M z

ql2

; Mmax

;

W z

b z h2

;

I z W z

h .

M z

По условию, max z

R :

b z

;

W z

max

200 кН/м 16 м2

30 см.

max

8 200 МПа

400 см

б) d 2

M z

2 ,

z 2R

z .

dz2

EI z

Eh 2

Учловия закрепления: 0

l 0

Rl2

200 МПа 16 м2

max

20 мм.

4Eh

4 200 ГПа 0,2 м

Ответ: b

30см;

2см вниз.

max

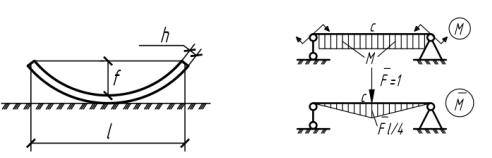
5.8.Определить прогиб и угол поворота произвольного сечения

впролете балки с постоянной жесткостью сечения, загруженной равномерно распределенной моментной нагрузкой интенсивно-

стью m (рис.5.8).

Решение

RA RB m, Q z RA m;

Рис.5.8	102

dM Q m,

z 0.

d 2

M z

z 0,

dz2

где 0 0 0 0;

l 0 0

ср z

0 k

ср z

Q z

Ответ: z 0;

φ z k

по часовой стрелке.

5.9. Стальной стержень прямоугольного сечения размерами b h и

длиной l свободно лежит на плоской опорной поверхности. Определить стрелу прогиба f при нагревании стержня, если температура по высоте стержня изменяется линейно и разность температур нижней и верхней грани равна t градусов (рис.5.9).

Рис. 5.9

Рис. 5.9(а)

Решение

M z

0 z l,

t z t tн tв;

;

t z

y h

t t

y :

1 t

;

M z

t z

M t

t .

1 l

f c

M M

EI 2

Ответ:

t l2

8 h

103

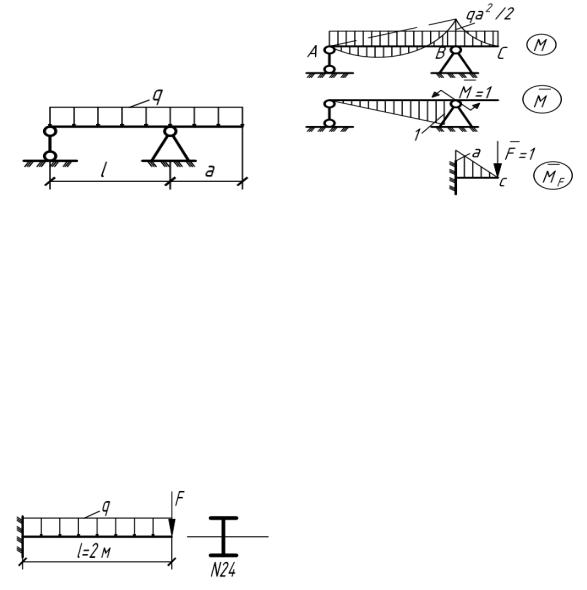
5.11. При какой длине консоли а угол поворота на правой опоре балки равен нулю? Чему равен в этом случае прогиб на конце консоли?

Рис. 5.11 Рис. 5.11(а)

Решение

1 ,

2 l ql2 1

qa2

M M

0 :

3 8 2 3 2

qa2

3 a

ql4

при a

M F

128EI

Ответ: a

;

ql4

вниз.

128EI

5.12. Какую силу F можно приложить в дополнение к распределенной нагрузке q = 6 кН/м, чтобы наибольшие нормальные напряжения не превышали 160 МПа, а наибольший прогиб (от тех же нагрузок)

не превосходил 1/250 пролета балки?

Решение

ДвутаврN24: W =289 см3

=3460 см4.

а) Mmax

maxWx ,

160 МПа 289 см3

6 кН/м 2 м

17,12 кН;

max

2 м

б) max

8EIx

3EIx

250

3EI

3ql

3 200 ГПа 3460 см4

3 6 кН/м 2 м

16,26 кН.

250

4 м2

Ответ: F 16, 26кН.

104

5.13. При каком значении коэффициента прогибы концов балки будут одинаковы? (рис.5.13).

Рис. 5.13

Рис. 5.13(а)

Решение

M M

a Fa 1a

Fa 4a 2a

0 : 1 2 2 0 .

Ответ: =2,5.

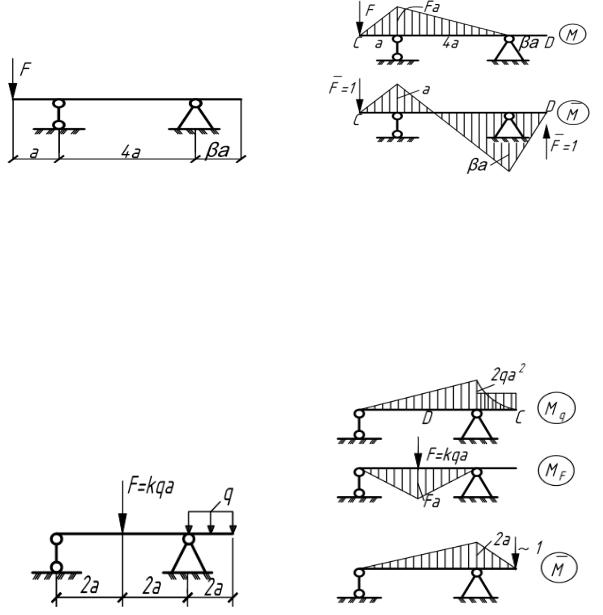
5.15. Определить коэффициент k, при котором прогиб конца консоли равен нулю. Чему при этом равен прогиб под силой F? (рис.5.15).

Рис. 5.15

Рис. 5.15(а)

Решение

а)

(Mq MF )M

EIx

4a kqa

4a 2qa

2a 2qa2

;

EIx

qa4

0 : k

;

EIx

105

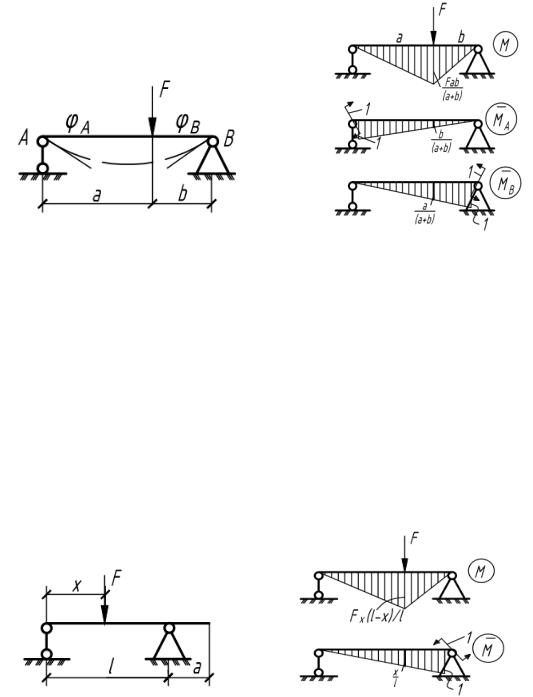
б) D

(M F M q )

M F

EIx

4a kqa2

2qa

qa4

2 .

EIx

Ответ:

;

qa4

вниз.

EIx

5.16. Найти отношение длин a/b, при котором соотношение углов поворота на опорах φА / φB = 2/3 (рис.5.16).

Рис. 5.16

Рис. 5.16(а)

Решение

Fab

a 2b

A dz

EIx

EIx a b

Fab

b 2a

B dz

EIx

EIx a b

A a 2b

;

A 2 :

a 4b.

b 2a

Ответ: ab 4.

;;

5.17. При каком значении координаты х подвижной нагрузки F прогиб конца консоли будет наибольшим? (рис.5.17).

Рис. 5.17

Рис. 5.17(а)

106

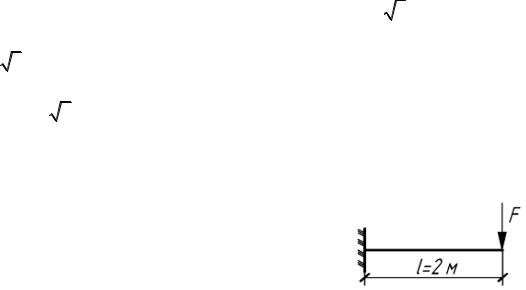
Решение

C B a,

0 x l;

l x

M dx

x l2 x2 ;

EIx

d B

;

d B

0 :

;

6l EIx

при x

max

тогда

max

Ответ:

0,577l.

5.19. Балка симметричного (относительно горизонтальной оси) сечения высотой h = 20 см изгибается под действием силы F . Наибольшие нормальные напряжения в поперечном сечении σmax = 150 МПа.

Найти прогиб и угол поворота на свободном конце, полагая Е = 105 МПа.

Решение

max

Mmax h

h ;

max

Fl3

max

2 150 МПа 4 м2

2 см;

3E Ix

3 105 МПа

0,2 м

3Eh

max

Fl2

max

150 МПа 2 м

0,015 рад.

2E Ix

105 МПа 0,2 м

Ответ: max 2см вниз; φmax 0,015рад по часовой стрелке.

5.20. Балка l = 1 м, свободно лежащая концами на двух опорах, под действием некоторой нагрузки изгибается по дуге окружности. При этом прогиб среднего сечения равен max = 6,25 мм. Определить вели-

чину модуля упругости материала и радиус кривизны оси при условии, что σmax =10 МПа, высота сечения h = 10 см.

Решение

M l2

1 м2

const,

max

20 м;

EIx

EIx 8

8 6,25 мм

8 max

max ,

E 2 max 20 м 2 10

МПа 4 ГПа.

E 4 ГПа.

0,1 м

Ответ: ρ 20м;

107

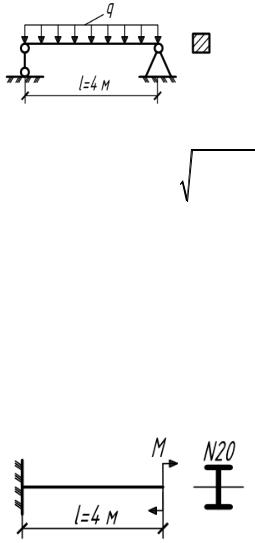
5.21. Балка квадратного сечения находится под действием распределенной нагрузки q=8 кН/м. Определить максимальный прогиб балки и радиус кривизны оси в среднем сечении,

WMmax

xmax

если в этом сечении max=12 МПа, а модуль

упругости Е= 10 ГПа.

			Решение
	l			ql2
0 z l,	M		Mmax		16 кНм;
0 z l,	M	2	Mmax	8	16 кНм;
		2		8

: a 3 6 Mmax 20 см;

max

M max	E	2	max	,	Ea	10 ГПа 0,2 м	83,3 м.
		a			2 max	12 МПа 2
Ix

	5ql4	5 8 кН/м 4 м 4 12	2 см.

max	384EIx	384 10 ГПа 0,2 м 4

Ответ: max 2см; ρ 83,3м.

5.22. Стальная двутавровая балка нагружена сосредоточенным моментом М, вызывающим σmax 100 МПа. Определить величину момен-

та, радиус окружности , по которой

изгибается балка, и прогиб на сво-

бодном конце max (рис. 5.22).

Решение:

Двутавр N20:

Рис. 5.22

W 184 см3, I

1840 см4;

W 100 МПа 184 см3

18,4 кНм;

max

200 ГПа 1840 см4

200 м;

18,4 кНм

max

Ml2

16 м2

4 см.

2EIx

2 200 м

Ответ: M 18,4 кНм;

ρ 200 м;

max 4 см.

5.23. При заданных величинах а и b определить отношение I1/I2, при котором прогиб сечения, где приложен момент M, равен нулю. Чему равен при этом угол поворота этого сечения (рис.5.23)?

108

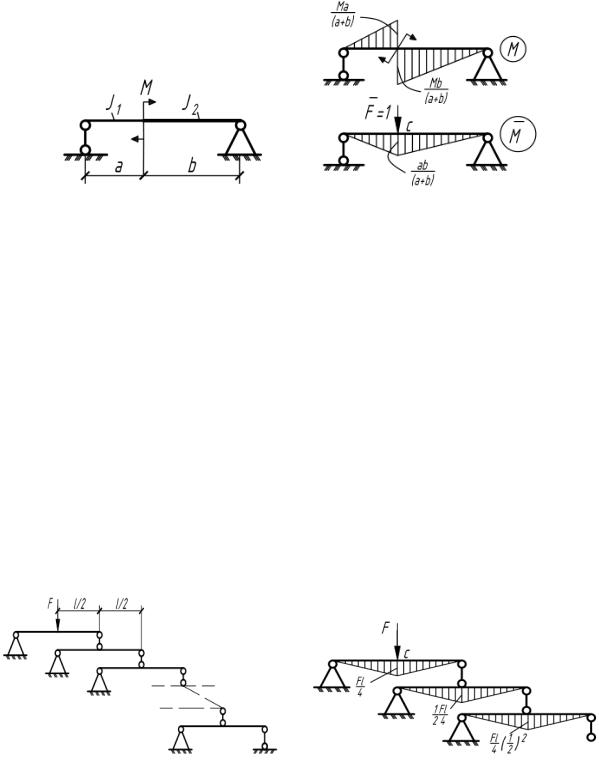
Рис. 5.23

Рис. 5.23(а)

		1
MM
C EI		dz
	i		EI
		1

C 0 :

Решение

;

a b

EI2

a b a b

;

a b

Mb3

1 .

3EI2

a b

Ответ:	I	1	a2	; φC	Mb2	.
	I2		b2		3EI2 a b

b	Mb	1b
	a b	a b
3

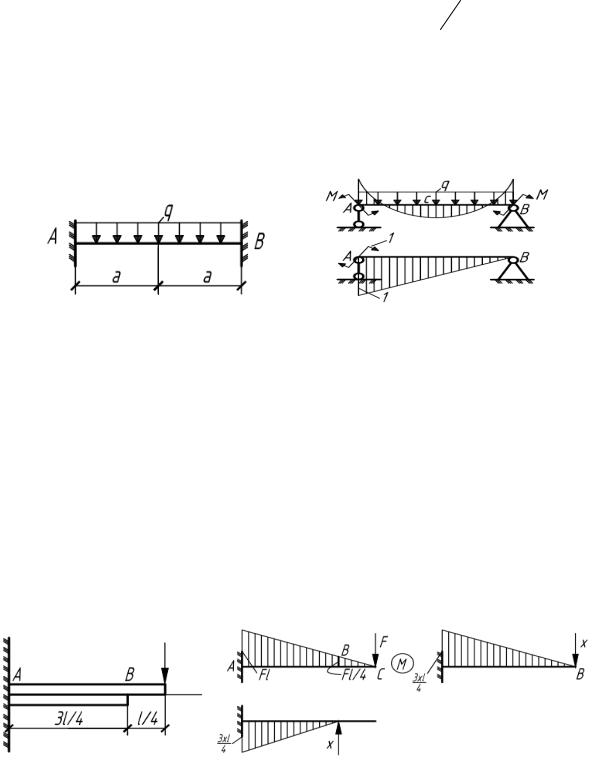
5.24. Определить прогиб точки приложения силы F для полубесконечной системы одинаковых балок длиной l и жесткостью ЕI

(рис.5.24).

	Рис. 5.24									Рис. 5.24(а)
					Решение
				Fl3		1 2	1	1	2		1	1	1 2
C		MM	dz	Fl3		1 2	1	1	2		1	1	1 2
					1
		EI		48EI	1			2			2	2
		EI		48EI		2	2	2			2	2	2

						109


	Fl3			1 1		1 2	1 3	Fl3		1		Fl3
		1											.
	48EI	1		4		4	4	48EI	1	1		36EI	.
	48EI			4		4	4	48EI	1	1	4	36EI
											4
Ответ: C			Fl3		.
Ответ: C			36EI		.
			36EI

5.25. Балка АВ защемлена по концам. На какие углы следует

повернуть обе заделки, чтобы после приложения нагрузки q моменты в сечениях А, В и С были одинаковы по абсолютной величине?

(рис.5.25)

Рис. 5.25

Рис. 5.25(а)

Решение

q 2a 2

M M A M B MC :

ql2

qa2

;

M q M M

M A

1 2l

qa3

EI 3

Ответ: φA

qa3

по ;

φB

qa3

по .

5.26. Две балки одинаковой жесткости EI соприкасаются во всех точках до нагружения и в точках А, В – после нагружения. Найти максимальный зазор, который образуется между балками под нагрузкой. Дано: F, EI, l. (рис.5.26).

Рис. 5.26			Рис. 5.26(а)
			Решение
1,B	M F M X M	dz
	EI1

110

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 1711 12 13 14 15 16 17 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.06.20248.07 Mб02377.pdf
#
17.06.20248.08 Mб02378.pdf
#
17.06.20248.08 Mб02379.pdf
#
17.06.2024243.89 Кб0238.pdf
#
17.06.20248.09 Mб02380.pdf
#
17.06.20248.13 Mб62381.pdf
#
17.06.20248.16 Mб02382.pdf
#
17.06.20248.23 Mб02383.pdf
#
17.06.20248.23 Mб02384.pdf
#
17.06.20248.23 Mб42385.pdf
#
17.06.20248.24 Mб02386.pdf