Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2381

.pdf

Скачиваний:

Добавлен:

17.06.2024

Размер:

8.13 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1710 11 12 13 14 15 16 17 > Следующая >>>

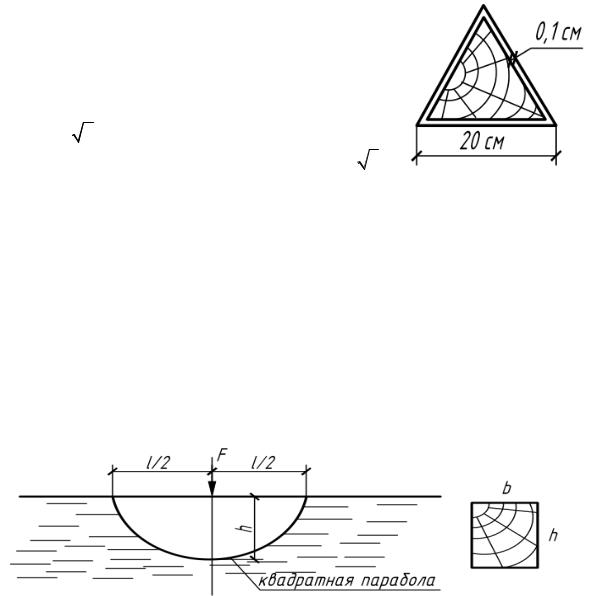
изгибающий

момент

выдерживает

брус,

если Rс 210 МПа,

R 14 МПа,

20Е

Решение

Нейтральная

ось

X центр

тяжести

тре-

угольника.

M 2

, т.к. M M1 M 2 ;

EдI1

EсI2

EдI

пр

, I

, y

пр

;

max

Rд

max

R :

E y

max

R :

Rс

15Rд

Rд

;

max

E y

max

20E y

max

E y

max

RдIпр

M E I

6,262 кНм.

пр

E y

max

Ответ:

M 6, 262 кНм.

4.65. Деревянный брус переменного сечения удерживает груз F на плаву. Определить σmax в среднем сечении балки. Как изменятся эти

напряжения при замене данной балки брусом постоянного сечения с шириной b, обладающим той же плавучестью?

Решение а) брус с высотой по квадратной параболе:

		2z 2		l				l
y z h 1			,		z				;
y z h 1			,	2	z			2	;
		l		2				2

l/2	y z bdz z					3
Mmax						3	Fl;
Mmax						32	Fl;
0						32
0

б) брус постоянного сечения:

2 hbl h bl,		h 2 h;
3	o	o	3

l/2

2 hbl;

F 2 y z bdz

max

Mmax

;

bh2

l/2

Mmax

Mmax hobdz z

Fl;

max

bh2

Ответ: σmax

; они возрастут в 3 раза.

bh2

4.66. Балка-консоль прямоугольного поперечного сечения нагружена на конце силой F. Ширина балки b постоянна, а высота меняется по линейному закону от h1 до h2 3h1. Установить положение опасного

(по ) сечения и определить величину σmax .

Решение

0 z l :

M x z Fz,

h z

, W

bh2

2z 2

max z

M x z

Fz 6

;

d max z

0 :

Wx z

bh2 1 2z

2z 2

2 1

Ответ: σmax

bh1

4.67. Балка-консоль, загруженная силой на свободном конце, имеет форму усеченного кругового конуса с диаметрами оснований d1 и d2 .

При каких соотношениях d1 / d2 наибольшее нормальное напряжение

возникает в заделке?

Решение

z 0 :

d z d d

z Fz,

W z

d d

M x z

d max z

max z

;

0 :

d d2 d1 z

z 3 d2 d1 0,

Wx z

2 d2 d1

При 0

max z возрастает.

2 d

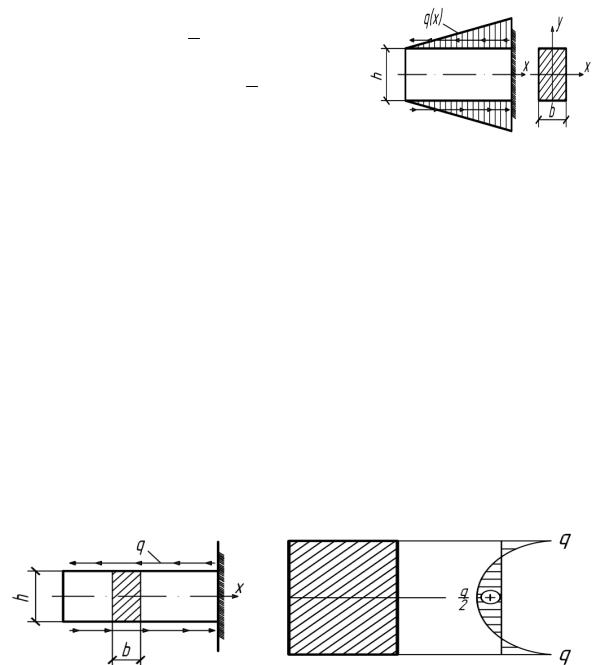
Если	z	1	или	d1	2	, то max z в заделке.
Если	l	1	или	d2	3	, то max z в заделке.
	l	d1	2 .	d2	3
Ответ:		d1
Ответ:		d2
		d2	3

4.68. По верхней и нижней поверхностям консольной балки прямоугольного поперечного сечения действует касательная нагрузка интенсивностью qz , распределенная вдоль оси балки z по линейному

закону, а по ширине b – равномерно. Установить характер изменения касательных напряжений в произвольном сечении.

Решение

0 z l : qz z qb zl ,

m z 2 qz z h2 qbh zl .

Из равновесия:

Q z 0, M z

m z z

qbh

;

Q m.

qz z

y h :

z, y

Sxотс

Ix b

qz z

отс

h Sx

где Ix

bh3

отс

y 2

Ответ: τ

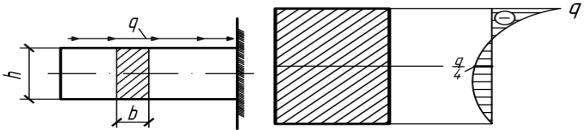
4.69. Для консольной балки вывести формулу для определения касательных напряжений, действующих в поперечном сечении, и построить их эпюру. Считать qz поверхностной касательной нагрузкой,

равномерно распределенной по ширине b и по длине l балки (рис.4.69).

Рис. 4.69

Рис. 4.69(а)

Решение

0 z l : qz z

qb,

m z 2 qz z

qbh.

Из равновесия:

Q z 0,

M z m z z qbh z;

Q m.

qz z

отс

y h :

z, y

q 1

h Sx

dz Ix b

h 2

q 1

где Ix

bh3

отс

y 2

Ответ: τ

(рис. 4.69(а)).

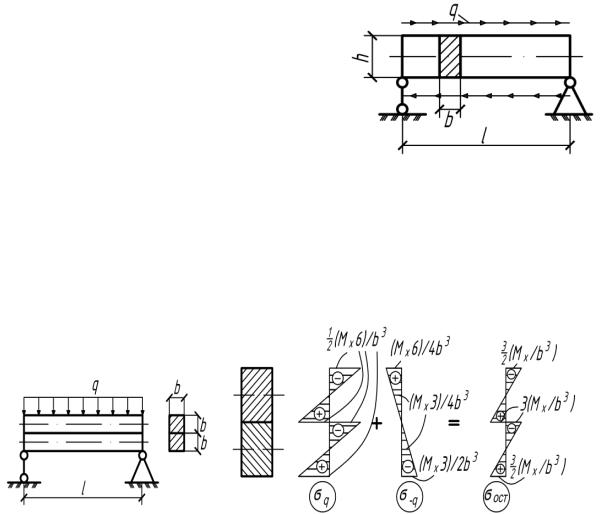
4.70. Вывести формулу для касательных напряжений, возникающих в прямоугольном поперечном сечении балки и построить их эпюру. Считать qz поверхностной касательной нагрузкой, равномерно

распределенной по ширине b и по длине l балки (рис.4.70).

Рис. 4.70		Рис. 4.70(а)
	Решение
0 z l : qz z qb,	m z qz z h	qbh .
Из равновесия:	2	2
Из равновесия:

N z qz z z qbz, Q z 0,		M z m z z qbh z;
			2
dN	qz z qb,	dM	Q m qbh .
dz		dz	2

h2 y h2 :

из равновесия отсеченной части элемента dz :

q b dz
		dN		dM y dA 0,
	Aотс		A	Ix

отс

q dN

q h

Ix b

dz A b

2 Ix

где Ix

bh3

отс

, A bh, Sx

	1	y			y 2
Ответ: τ q			3			(рис. 4.70(а)).
Ответ: τ q	4	h	3			(рис. 4.70(а)).
	4	h		h

1 ,

4.71. Записать выражения для напряжений и в произвольной

точке балки. Считать q поверхностной касательной нагрузкой, равномерно распределенной по ширине b и по длине l балки.

Решение

m 2qb h ;

R R

ml ;Q z R

M z 0 :

y 0;

Sотс

Q m 0 :

q q.

Ix b

τ q.

Ответ: σ 0;

4.72. Две стальные балки сечения b b свободно уложены друг на

друга. После загружения нагрузкой q балки по длине свариваются. Как распределяются остаточные напряжения в балках после снятия нагрузки? (рис.4.72).

Рис. 4.72

Рис. 4.72(а)

Решение a) несваренные балки от q z q :

1	M1	M2	M x	, т.к. M x M1 M2 ,

	EI1	EI2	EI1 EI2

: M

ql2 z

z 2

x,max

, W

x , i

1,2;

б) сваренные балки от q z

q :

ql2 ; 8

x ,

8b4

M x

ql2 z

, M x,max

ql2

;

x ,

4b3

;

в) сваренные балки от q z q q 0

остаточныенапряжения :

b y b :

при y b,

ост

Mx,max

;

M x,max

при y 0,

ост

3ql2

6ql

Ответ:

y b :

σост

;

y 0

σост

16b3

4.73. Стальная шарнирно опертая по концам балка имеет сечение в форме равностороннего треугольника со стороной a. Балка загружена силой F , приложенной в среднем сечении и медленно вращающейся в плоскости этого сечения. Найти a, если R= 200 МПа, F= 30 кН, l=2 м.

Решение

Ix I y Iu

; M max

;

ymax

2 a

;

max

Mmax

ymax

8Fl

R :

a 3

8Fl

13,4 см.

Ответ: a 13,4 см.

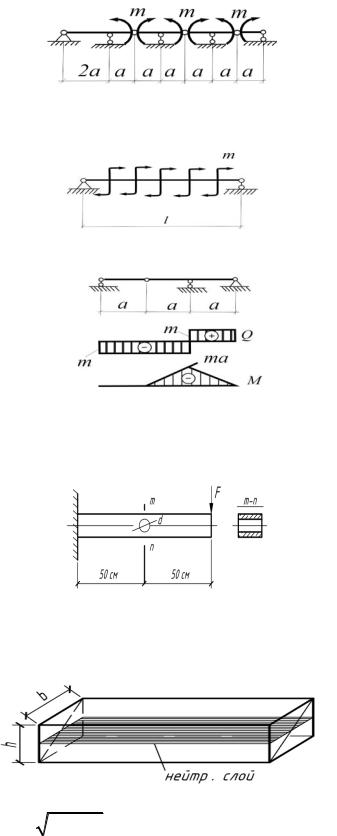
Задачи для самостоятельного решения

1. Для заданной балки построить эпюры Q и М.

2. Построить эпюры Q и М. Объяснить, почему в этом с соблюдается дифференциальная зависимость Q = dM/dx.

3.Для заданной балки определить нагрузку по эпюрам Q и М.

4.Деревянный брус квадратного сечения 6 6 см выдерживает

нагрузку 360 H. Снизится ли несущая способность балки, если в ней просверлить отверстие диаметром d=4 см в сечении m-n? Концентрацию напряжения не учитывать.

Ответ: нет, т.к. σ1 σ2 .

5. Балкасклеенаиздвухтреугольныхпризм(рис.4.33). Определить

касательноенапряжениевплоскостисклейкинауровненейтрального слоя.

Ответ: max	b		.
	h2	b2

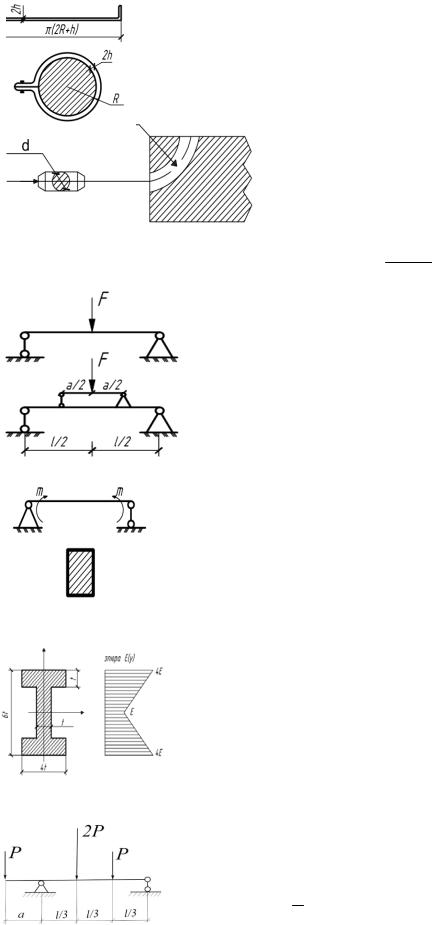
6. Найти максимальное напряжение в стальной ленте толщиной 2h=1 мм и длиной (2R+h), огиба-

ющийцилиндррадиусаR = 100 см, еслиE = 2 105 МПа.

Ответ: σmax 150 МПа.

7. Круглый стержень диаметром d проталкивается по криволинейному каналуr, сделанномувабсолютнотвер-

дом теле. Каков должен быть rmin , чтобывстержненевозникалинапряжения более чем σmax ? Трением пренебречь.

Ответ: rmin 2σEd .

max

8. Наибольшие нормальные напряжения в поперечном сечении балки, нагруженной силой F, на 25% выше расчетного сопротивления R. Чтобы снять напряжение, устанавливается вспомогательная балочка. Найти ее минимальную необходимую длину a, считая величину l заданной.

Ответ: amin 0, 2l.

9. Резиновый брус прямоугольного сечения 10 15 см плотно помещен в стальную обойму толщиной =2 мм. Пользуясь гипотезой плоских сече-

ний, определить значение изгибающего момента, разрушающего обойму, если предел прочности материала обоймы σu =500 МПа.

Ответ: Mmax 23, 5 кНм.

10. Модуль упругости материала балки двутаврового поперечного сечения изменяется по указанному на рисунке закону. Какой наибольший изгибающий момент может выдержать такая балка по условию прочности при чистом изгибе в плоскости наибольшей жесткости?

Ответ: M x 976 Rt3 .

11. Найти соотношение длин а/l, при котором значение максимального изгибающего момента в балке будет наименьшим.

Ответ: a 3l .

Глава 5. ПЛОСКИЙ ПОПЕРЕЧНЫЙ ИЗГИБ (ПЕРЕМЕЩЕНИЯ)

Краткие теоретические сведения Основные понятия и обозначения

Параметры, определяющие поле перемещений в балках:

–z прогиб, т.е. поперечные перемещения точек на оси стержня;

–z угол поворота поперечного сечения стержня.

Рассматриваются малые, упругие деформации. Справедлива Г.П.С.:

z	d	без учета деформаций сдвига ;
	dz
					ср z			Q z
z	d	ср z	d	k		d	k		.
	dz		dz		G	dz		GA

Приближенное дифференциальное уравнение изогнутой оси балки:

1	M	d 2	, где d dz, т.е.	d	1	dz,
	EI	dz2

z радиус кривизны нейтрального слоя стержня.

Универсальное уравнение изогнутой оси балки при EIx const :

z z

z z j 3

z z

EI z EI 0 EI 0 z Mi

24 .

Определение перемещений методом Мора:

iF Mi

dz,

где iF проекция полного перемещения на i -е направление от внешней нагрузки F и t tв tн (причина);


M F "грузовая" эпюраM от внешней нагрузкиF;
	i "единичная"эпюраM отединичногоусилияпо i - мунаправлению
M
приопределении		от		1,		1 ;
			F
					φ отM
EI "изгибная"жесткостьстержня;							h толщинастержня.

Примечание. При определении взаимного перемещения двух точек необходимо построить эпюру Mi от единичных усилий, приложенных

одновременно в этих точках в противоположных направлениях.

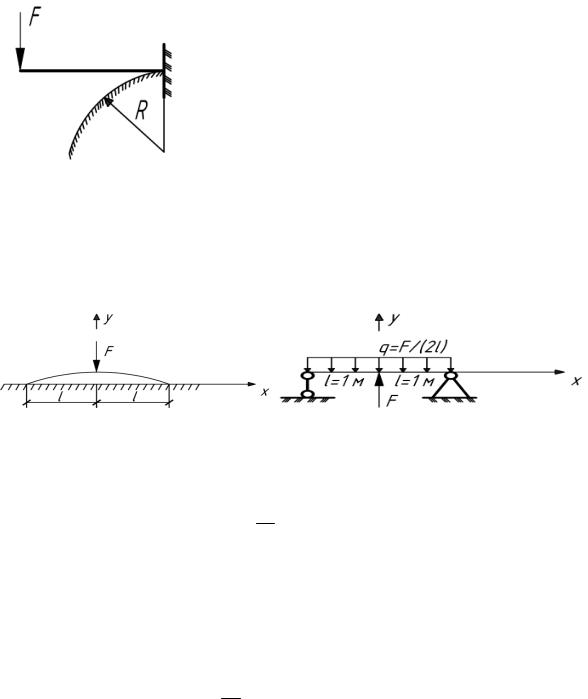
Примеры решения задач

5.2. Плоская стальная пластина толщиной = 2 мм изгибается си-

лойF, касаясьприэтомкруглогоцилиндрарадиусаR = 1 м. Определить наибольшее нормальное напряжение в изогнутой пластине.

Решение

R M

EIx ;

EIx

max

ymax

R Wx

200 ГПа

1 мм.

1 м

Ответ: σmax 200 МПа.

5.3. Какую первоначальную форму следует придать стальной пластине прямоугольного сечения 6 1 см и длиной 2l = 2 м, чтобы под

действием силы F = 480 Н она полностью соприкасалась с гладким жестким основанием и давление равномерно распределялось по длине балки? Чему равно σmax ? (рис.5.3).

Рис. 5.3

Рис. 5.3(а)

Решение Обратная задача: Положениеизогнутойоси(доизгибаось прямая), если

F 480 Н, q 2Fl 240 Н/м, RA RB 0.

Начало координат на оси симметрии: 0 x l,

q q,	Q	F	,	M	0	ql2	Fl	,	0	0,		y 0;

0	0	2				2	4					0
				l 0,							y l 0.
Q l 0, M							l 0,

Универсальное уравнение изогнутой оси балки (М.Н.П.):

EIy x EIy0 EI 0 x M0 x22

y l 0 :	EIy Fl3
	0	16
		16


Q0		x	3	q0	x	4	EIy0				Fx			2		l		x		x	2
		x			x						Fx					l		x		x		;
		6			24							4				2						;
		6			24							4				2		3		12l
	EIy x					Fl		3	Fx	2			l		x		x	2
						Fl			Fx				l		x		x		.
						16			4						3		12l		.
						16			4			2			3		12l

100

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1710 11 12 13 14 15 16 17 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.06.20248.07 Mб02377.pdf
#
17.06.20248.08 Mб02378.pdf
#
17.06.20248.08 Mб02379.pdf
#
17.06.2024243.89 Кб0238.pdf
#
17.06.20248.09 Mб02380.pdf
#
17.06.20248.13 Mб62381.pdf
#
17.06.20248.16 Mб02382.pdf
#
17.06.20248.23 Mб02383.pdf
#
17.06.20248.23 Mб02384.pdf
#
17.06.20248.23 Mб42385.pdf
#
17.06.20248.24 Mб02386.pdf