Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2381

.pdf

Скачиваний:

Добавлен:

17.06.2024

Размер:

8.13 Mб

Скачать

☆

1 / 171 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

_______________________

Федеральное государственное бюджетное образовательное учреждение высшего образования «Пензенский государственный университет архитектуры и строительства»

(ПГУАС)

В.П. Волков

СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ

Учебно-методическое пособие для практических занятий по направлениям подготовки

08.05.01«Строительство уникальных зданий и сооружений»,

08.03.01«Строительство»

Пенза 2016

УДК 539.3/6(075.8) ББК 30.121я73

В67

Рецензенты: главный конструктор ОАО «Приволжское КБ», кандидат технических наук, доцент В.М. Машин; заслуженный строитель РФ, кандидат тех-

нических наук, профессор В.С. Абрашитов (ПГУАС)

Волков В.П.

В67 Сопротивление материалов: учебно-методическое пособие для практических занятий по направлениям подготовки 08.05.01 «Строительство уникальных зданий и сооружений», 08.03.01 «Строительство» / В.П. Волков. – Пенза: ПГУАС, 2016. – 164 с.

Приведены краткие теоретические сведения, примеры решения обычных и нестандартных, требующих при решении оригинального подхода задач, и задачи для самостоятельного решения по различным разделам курса сопротивления материалов.

Учебно-методическое пособие подготовлено на кафедре «Механика» и предназначено для студентов, изучающих курс «Сопротивление материалов», обучающихся по направлениям подготовки 08.05.01 «Строительство уникальных зданий и сооружений», 08.03.01 «Строительство». Также оно может быть полезно аспирантам, исследующим вопросы расчета элементов зданий и сооружений на прочность и жесткость, и преподавателям курсов «Сопротивление материалов» и «Техническая механика».

©Пензенский государственный университет архитектуры и строительства, 2016

©Волков В.П., 2016

ПРЕДИСЛОВИЕ

Сопротивление материалов – наука о прочности, жесткости и устойчивости стержня, т.е. одного из основных элементов строительных конструкций. Умение определять напряженно-деформированное состояние стержня от действия различных внешних силовых, деформационных и температурных воздействий является необходимым требованием к инженеру.

Вучебно-методическом пособии рассмотрен один из возможных вариантов решения представленных задач. В основном в данном пособии рассмотрены задачи из [3], т.е. как стандартные, так и задачи повышенной трудности, такизадачи, требующиенестандартногооригинальногоподхода

ких решению, так и задачи показывающие ограниченность некоторых стандартных подходов, правил и теорем. Как и в [3], задачи сгруппированы по темам, относящимся к различным разделам сопротивления материалов. Краткие теоретические сведения и формулы, необходимые при решении задач по данной тематике, приведены в виде справочника в начале каждого раздела. Разбор примеров решения таких задач значительно помогает студентам самостоятельно освоить основные разделы сопротивления материалов. В конце каждого раздела представлены задачи для самостоятельного решения с ответами.

Вучебно-методическом пособии рассмотрено более трехсот задач, которые могут быть использованы как при проведении практических занятий по сопротивлению материалов и технической механике, так и при проведении олимпиад по сопротивлению материалов и при организации учебно-исследовательской работы студентов, в кружках, а также студентами и преподавателями, интересующимися задачами необычного типа с целью углубить свои знания по сопротивлению материалов.

Глава 1. РАСТЯЖЕНИЕ (СЖАТИЕ) ПРЯМОГО СТЕРЖНЯ

Краткие теоретические сведения

Основные понятия и обозначения

u u z продольное перемещение поперечного сечения стержня;z относительная линейная или продольная деформация; N N z продольная сила в поперечном сечении стержня;

A A z площадь поперечного сечения стержня;

dz абсолютная деформация или приращение элемента dz.

Напряженное состояние а) дифференциальнаязависимостьвнутреннихусилийотвнешнейнагрузки:

dNdz qz , N z qzdz N0;

б) напряжения в произвольной точке поперечного сечения стержня:

0;	N	это линейное напряженное состояние;
	A

в) условие прочности материала стержня:

max R.

Деформированное состояние

dz относительная линейная деформация элемента dz; dz

t t деформация элемента dz от изменения температуры t.

Определение перемещений а) при упругой деформации зависимость из закона Гука:

E ;

б) методом непосредственного интегрирования:

u z

dz u ;

в) по формуле Мора:

t t dz,

где iF проекция полного перемещения на i-е направление от внешней

нагрузки F и t tв tн t0 (причина);

NF "грузовая" эпюраN от внешней нагрузкиF;

Ni "единичная" эпюра N от единичного усилия по i-мунаправлению. Потенциальная энергия упругой деформации

	N dz	N 2			1	N 2
U			dz,	U	2		dz.
	2	2EA				EA

Примеры решения задач

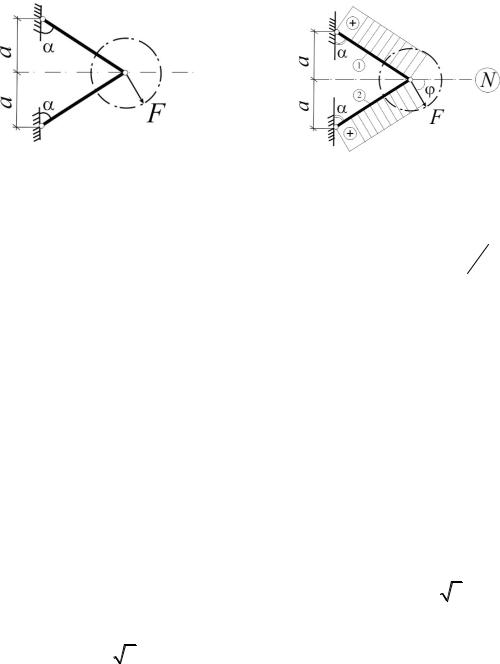
1.1. Сила F совершает медленное вращательное движение в плоскости стержневой конструкции. Определить из условия прочности угол, при котором конструкция будет иметь наименьший вес. Размер а задан.

Рис. 1.1

Рис. 1.1 (a)

Решение

Из равновесия узла:

F cos

sin

cos

sin 2

sin

cos

F cos

sin

cos

sin 2

sin

cos

0 2

0 2 n

0 2 :

Ni Nmax , если

cos

1: Nmax F / sin 2 ;

max

Nmax

R : A

Nmax

, V A l

Rsin 2

cos

Т.к.

V Vmin , если V ' 0 , тогда

V 0 :

F a 1

cos 2 2cos sin 2 sin 0,

sin 2 cos 2

tg 2 tg 2

2tg

tg 2

, tg2 1

, tg

tg2

Ответ: arctg

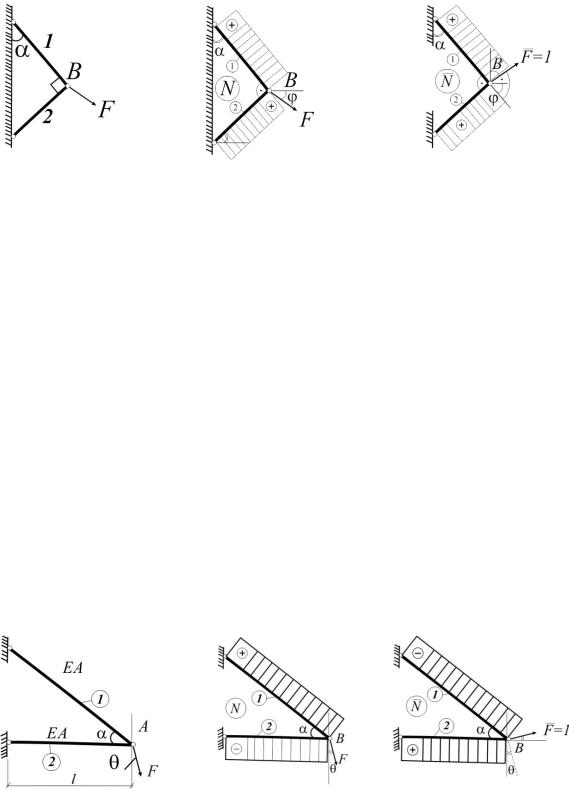
1.2. Дано: Е1А1 = Е2А2. Определить, при каком значении угла α

перемещение узла В будет совпадать с линией действия силы F. Сила F действует в плоскости фермы в любом направлении (рис.1.2).

Рис. 1.2

Рис. 1.2 (а)

Рис. 1.2 (б)

Решение

Из равновесия узла:

N F

sin cos sin cos F sin

0 / 2

;

cos cos sin sin F cos

, где

N2 F

0 2

F sin sin cos cos F cos

sin

cos sin sin cos F

Ni N

ds 0 :

E A

i i

l cos F sin cos l sin F cos

sin 0,

E A

sin cos .

Ответ: / 4.

1.4. Определить, какая зависимость должна быть между углами α и θ, чтобыперемещениеузлаАбылонаправленополиниидействиясилы

F (рис.1.4).

Рис. 1.4

Рис.1.4 (а)

Рис. 1.4 (б)

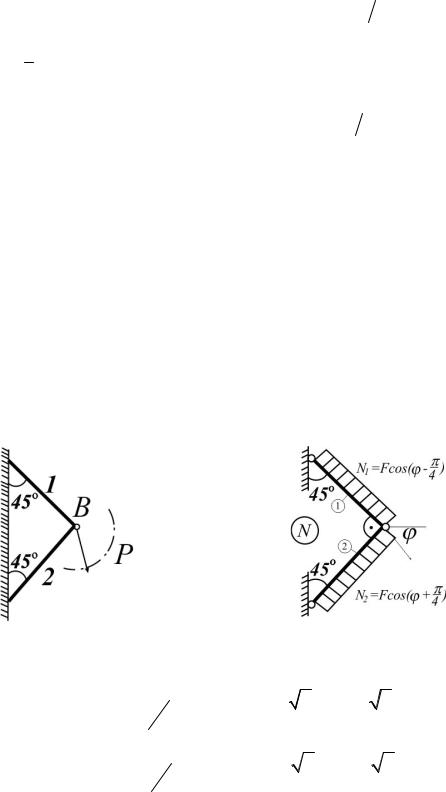
Из равновесия узла:

Решение

N F cos

sin

;

cos

F cos

cos

sin

cos

F sin sin

F cos sin

sin

B NNEA

ds 0 :

F cos

sin

cos

sin

cos EA

sin

sin 2

2cos

Ответ: sin 2θ cosαsin 2 θ α 0.

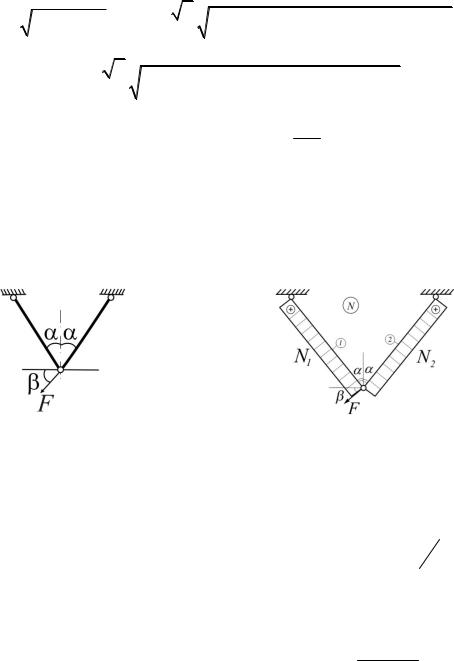
1.5. Дано: Е1А1 = Е2А2. Сила F, действующая в плоскости фермы, совершает поворот на 360°. Определить, какую траекторию при этом описывает узел В в результате деформации стержней 1 и 2 (рис.1.5).

		Рис. 1.5										Рис. 1.5(а)
						Решение
		l	F cos	4				Fl			2		2
		l				1		Fl	cos		2	sin	2
						1			cos			sin
	1B	EA1					EA				2		2	,	0	2 .
		l	F cos		1			Fl			2		2
		l						Fl			2		2
2B				4						cos		sin
2B		EA2								cos	2	sin	2
		EA2						EA			2		2

B	2	2			Fl		2	cos sin 2				cos sin 2
	2	2						cos sin 2				cos sin 2
	1B		2B		EA	2
					EA	2
			Fl	2	cos	2			2	cos	2		2	Fl
							φ sin					φ sin			.
			EA	2			φ sin					φ sin		EA	.

Ответ: окружность вокруг В с радиусом EFAl .

1.6. Сила F может быть приложена в плоскости чертежа под любым углом β. Подобрать площади сечения стержней фермы из условия прочности. R = 100 МПа, F = 20 кН, α = 30°. Снижение расчетного сопротивления при сжатии не учитывать (рис.1.6).

Рис. 1.6

Рис. 1.6 (а)

Решение

Из равновесия узла:

F sin

cos

sin 2

2 cos

sin

F sin

cos

sin 2

2 cos

sin

Nmax , если

cos

1 Nmax

,0 20 2

sin F2 .

max	Nmax	R : A	Nmax	F	2,3 см2.

	A		R	Rsin 2

Ответ: 2,3 см2.

1.7. На узел B кронштейна, состоящего из стержней ВС и BD одинакового поперечного сечения А = 5 см2, подвешен груз F = 30 кН. Под действием груза F узел В сместился вправо на и = 1,6 мм и опустился вниз на υ = 10,5 мм. Определить модули продольной упругости материалов cтержней EBC и EBD , если lBC = 5 м, lBC = 4 м (рис.1.7).

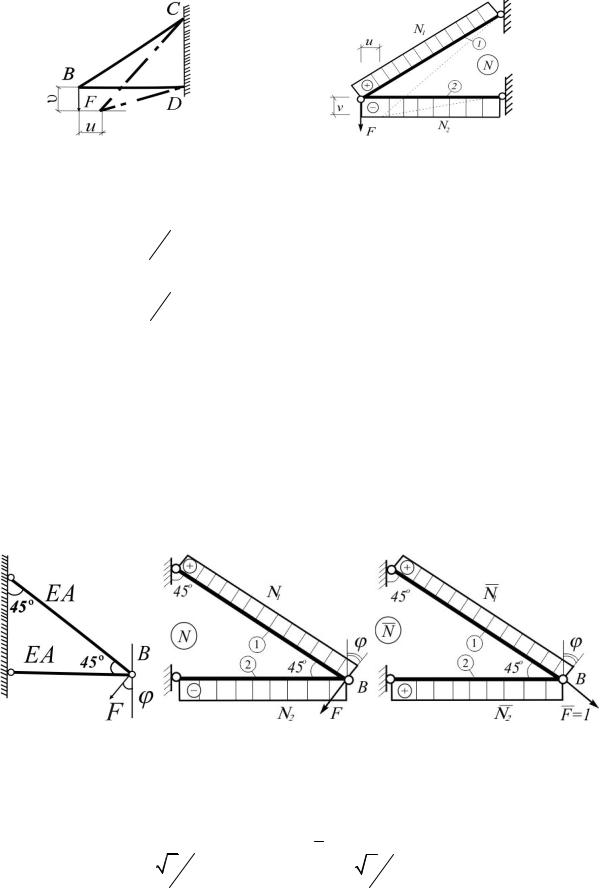
Рис. 1.7

Рис. 1.7(а)

Решение

5 / 3

4 / 3

3 F

5 м

4 м

;

E1A

E2 A

;

4 / 3

2 F 1

3 F

4 м

E2 A

E1 A

4 / 3 F 4 м

4 / 3 30 кН 4 м

200 ГПа

u A

1,6 мм 5 см

5 / 3

кН 5

100 ГПа

8,37 мм 5 см2

Ответ: 200 ГПа, 100 ГПа.

1.8. Определить, при каком значении угла φ перемещение узла В будет следовать по направлению силы F (рис.1.8).

Рис. 1.8

Рис. 1.8(а)

Рис. 1.8(б)

Решение

Из равновесия узла:

N		F cos			N
		F cos					F	sin
		2					2
	1	2		;		1	2			.
			2	;					2	.
			2						2
	N2 F sin cos
						N2 F cos sin
						N2 F cos sin

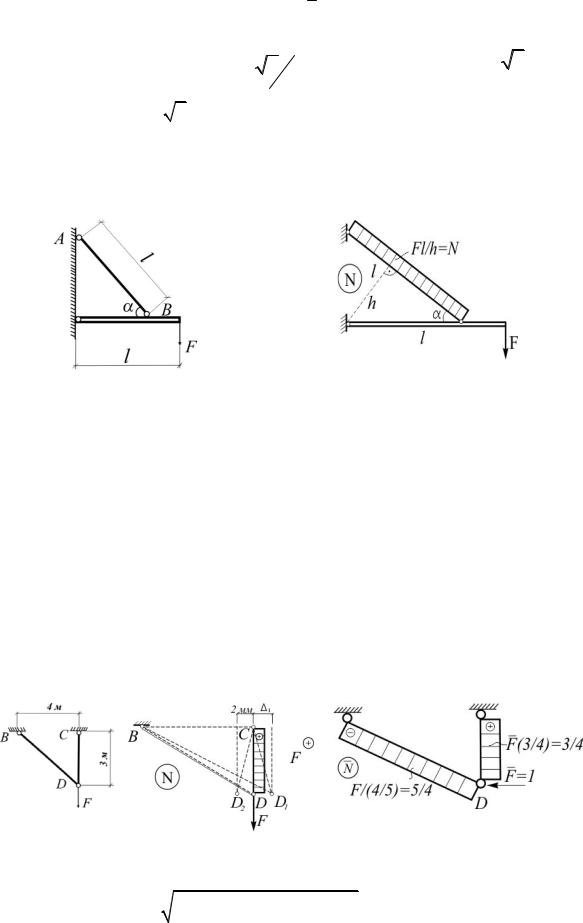
B NNEA ds 0 :

1			l F sin 2				1		l	2	2	F cos 2 0,	tg 2	2	.
	EA		l F sin 2			EA			l	2		F cos 2 0,	tg 2	2	.
	EA			arctg 2 /		EA								2
Ответ:		φ		arctg 2 /	2			.
Ответ:		φ		2				.
				2

1.10. Под каким углом α нужно установить тягу АВ длиной l, чтобы напряжения в ней были минимальными (рис.1.10)?

Рис. 1.10 Рис. 1.10(а)

Решение

		N Nmin , если		h hmax .
S	l h	l sin l cos	l2	sin 2 , h	l	sin 2 .
	2	2	4		2

h hmax , если sin 2 1, / 4.

Ответ: .

1.11. При сборке кронштейна BDC оказалось, что стержень DВ; имеет длину, превышающую проектную на 3,2 мм. Поэтому узел D сместился вправо. После загружения узла силой F он сместился влево на 2 мм от вертикали CD. Определить силу F, если материал стержней имеет модуль упругости Е = 2 105 МПа, площадь сечения стержней

А = 4 см2 (рис.1.11).

Рис. 1.11 Рис. 1.11(а) Рис. 1.11(б)

	Решение
	5 м 3,2 мм 2 3 м 2 4 м 4 мм.
1

1 / 171 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.06.20248.07 Mб02377.pdf
#
17.06.20248.08 Mб02378.pdf
#
17.06.20248.08 Mб02379.pdf
#
17.06.2024243.89 Кб0238.pdf
#
17.06.20248.09 Mб02380.pdf
#
17.06.20248.13 Mб62381.pdf
#
17.06.20248.16 Mб02382.pdf
#
17.06.20248.23 Mб02383.pdf
#
17.06.20248.23 Mб02384.pdf
#
17.06.20248.23 Mб42385.pdf
#
17.06.20248.24 Mб02386.pdf