988

0

d мкм

Рис. 2.19. Гранулометрический состав механических примесей: 1 – накопленная частость; 2 – частость [6]

Рис. 2.20. Метод геометрического определения по известным d и Рd [105]

72

На основании вышеизложенного, можно заключить, что на экономическую эффективность систем очистки СОЖ от механических примесей на технологических линиях механической обработки заготовок влияют следующие факторы:

1.Собственные технико-экономические показатели системы очистки, т.е. соотношение “степень (качество) очистки СОЖ – стоимость системы”

(см. рис. 2.4, 2.12 – 2.14).

2.Соотношение затрат по операциям технологической линии. Необходимо прежде всего обеспечить технологические эффекты для наиболее дорогостоящих операций ТЛ (см. рис. 2.7, 2.8).

3.Соотношение затрат на выполнение операции. Необходимо обеспечить технологические эффекты по наиболее значимым составляющим технологической себестоимости операции (см. формулу (2.30)). При определенном сочетании вышеперечисленных факторов более эффективной может оказаться сравнительно дешевая система очистки СОЖ, обеспечивающая худшую степень (качество) очистки, но наименьшие суммарные затраты на механическую обработку заготовок на технологической линии.

2.3.Расчет параметров чистоты СОЖ и характеристик очистителя для обеспечения оптимального сочетания

критериев технологической эффективности

Различные очистители обеспечивают разные параметры чистоты СОЖ

(С, d , ), оказывая тем самым влияние на производительность механической обработки и выходные показатели качества обработанных деталей, изменяя при этом критерии Кji и, в конечном итоге, экономическую эффективность технологической операции или линии в целом. После определения оптимального сочетания критериев Кji для линии (см. п. 2.2), необхо-

димо установить параметры чистоты СОЖ (С, d , ), которые обеспечили бы это сочетание. Для этого нужно знать характеристику очистителя d – степень очистки СОЖ по размеру частиц d, среднюю степень очистки.

Влияние чистоты СОЖ на изменение технологических показателей можно описать в общем виде:

где Хi – изменение параметра на i-ой операции;

Со – остаточная концентрация механических примесей в СОЖ после ее очистки, г/л;

d о – средний размер частиц механических примесей, оставшихся в СОЖ после ее очистки, мкм;

73

о – среднее квадратическое отклонение размеров частиц, оставшихся в СОЖ после ее очистки, мкм;

fki – функциональная зависимость критерия технологической эффективности Кi от параметров чистоты СОЖ.

Для проектирования системы очистки СОЖ, обеспечивающей требуемое (оптимальное) сочетание критериев Кi, необходимо установить взаимосвязь Кi и параметров чистоты СОЖ. Для этого можно воспользоваться зависимостями, приведенными в табл. 1.4, или выявить их экспериментально в производственных или лабораторных условиях, что и будет сделано далее в разд. 4.

Определим требуемые параметры чистоты СОЖ на выходе из системы

очистки Со, d о, o. Остаточную концентрацию механических примесей в СОЖ найдем по формуле:

где – степень очистки СОЖ в отдельном устройстве или в системе, %; Си – исходная концентрация механических примесей в СОЖ, г/л. Обозначим число частиц механических примесей, поступивших в

очиститель и оставшихся в СОЖ после ее очистки, соответственно через mи и mo. Тогда:

Исследованиями [6, 28 и др.] установлено, что степень очистки d является вероятностной величиной, распределенной по логарифмически-нор- мальному закону (рис. 2.18). Гранулометрический состав механических примесей также близок к логарифмически нормальному распределению частиц по размерам (рис. 2.19) с плотностью вероятности

(2.42), зависит от параметров чистоты СОЖ С, d , и характеристики очистителя d:

74

При этом возникает задача расчета характеристик очистителя , d и

параметров чистоты СОЖ Со, d о, o.

Известен метод Allander C.G. [105] геометрического определения средней степени очистки СОЖ от механических примесей , обеспечиваемой определенным очистителем при известных d и Рdи, распределенных по логарифмически нормальному закону (рис. 2.19).

Влогарифмической вероятностной плоскости (ордината градуирована по функции Лапласа (х) стандартного нормального закона, а абсцисса –

lnd) зависимости d и Pdи изображены прямыми линиями AF и FD соответственно (см. рис. 2.20). Из точки F опускают перпендикуляр FB к AD до точки Е, так что |BE| = |BD|. Затем строят точку С так, что |AC| = |AE|. Из точки С восстанавливают перпендикуляр GC к AD так, что |CG| = |BF|. Через точки А и G проводят прямую до пересечения в точке Н с перпендикуляром к АD, восстановленным в точке D. Ордината точки Н и есть

80 % данного очистителя.

Вобщем случае и функции распределения Pdo и Pdy могут быть найдены по следующим зависимостям:

где Pdy – функция распределения частиц механических примесей по размерам удаленных очистителем из СОЖ.

На основании данных [105] d и Pdи описываются логарифмическим нормальным распределением с большой точностью и имеют следующий вид:

75

Известно, что для логарифмического нормального распределения с плотностью вероятности

математическое ожидание и дисперсия равны соответственно:

интегралов:

Предположим, что Pdo и Pdи будут также иметь логарифмическое нормальное распределение. Если рассмотреть систему координат ( , ) на плоскости, где = lnd, = -1 (-1 – функция, обратная функции Лапласа ), то зависимости (2.47) и (2.47) примут линейный вид:

76

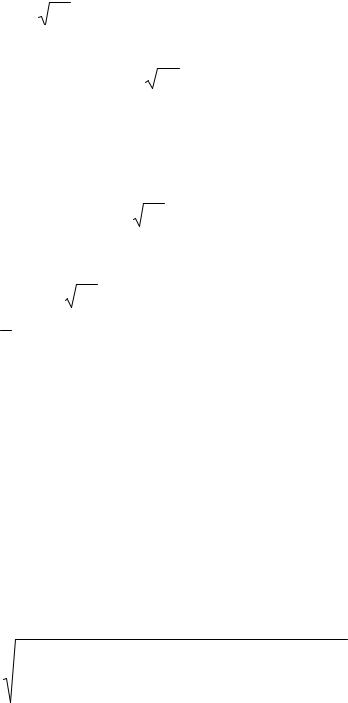
Таким образом, на логарифмически-нормальной плоскости d и Pdи

соответственно.

Получим распределение Pdy частиц механических примесей, удаленных очистителем. По предположению:

Подставим u = dи в последнее выражение, чтобы получить размер исходных механических примесей в точке математического ожидания, т.е. в наиболее вероятном случае:

Тогда

77

Зависимость (2.56) показывает, что средний размер удаленных частиц механических примесей dy будет всегда больше среднего размера dи

частиц примесей до очистки СОЖ (исходных), что согласуется со здравым смыслом.

Найдем функцию распределения Pdo для оставшихся в СОЖ частиц механических примесей:

Так как d – величина произвольная, то подинтегральные функции

Как следует из зависимости (2.57), средний размер оставшихся в СОЖ

частиц do будет всегда меньше размера частиц механических примесей dи до очистки (исходных).

78

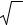
Сравнение результатов расчетов по формулам (2.56), (2.57) для разныхo и y с точными значениями, полученными по уравнениям (2.45), (2.46) позволило восстановить функциональные зависимости:

– если и y, то

–если и то функции распределения Pdo и Pdу имеют вид гипербол,

афункции распределения Pdи и d – вид асимптот. В этом случае нельзя с малой погрешностью приблизить данные функции распределения к логарифмически нормальным, следовательно, формулы (2.56)-(2.59) применить нельзя.

Поступим следующим образом. Пусть Fd и Gd – две функции распре-

деления на ( ), a fd и gd – соответствующие плотности вероятностей. Рассмотрим интеграл

Интеграл J записан как повторный интеграл для повторного интеграла. Изменим порядок интегрирования:

Таким образом, проблема нахождения Pdy и Pdo при и решена, так

как Pdy хорошо описывается логарифмическим нормальным законом

распределения , и

79

Если функции d и Pdи совпадают, то имеет место следующее

Отметим, что в этом случае = 0,5. Распределение Pdo

обратные задачи, т.е., зная любые три функции распределения из ряда d, Pdи, Pdy, Pdo и необходимо найти два остальных распределения.

1. Пусть известны Pdo, lnd o, o, Pdy, lnd y, y, . Необходимо найти

ln d и, и, ln d ,

Обозначим = 0,25333; = – 0,26874. Выразим из (2.58) величину :

80