
983
.pdfМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
________________________________________
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Пензенский государственный университет
архитектуры и строительства» (ПГУАС)
И.А. Гарькина, А.М. Данилов
СПЕЦИАЛЬНЫЕ РАЗДЕЛЫ ВЫСШЕЙ МАТЕМАТИКИ
Рекомендовано УМО РАЕ по классическому университетскому образованию в качестве учебного пособия для студентов высших учебных заведений,
обучающихся по направлению подготовки 08.04.01 – «Строительство»
Пенза 2014
1
УДК 51 (07)
ББК 74.58:22.1я73 Г20
Рецензенты: кафедра высшей и прикладной математики ФГБОУ ВПО «Пензенский государственный университет» (зав. кафедрой – доктор физико-математических наук, профессор И.В. Бойков); доктор физико-математических наук, про-
фессор О.А. Голованов (Пензенский артиллерийский инженерный институт)
Гарькина И.А.
Г20 Специальные разделы высшей математики: учебное пособие / И.А. Гарькина, А.М. Данилов. – Пенза: ПГУАС, 2014. – 160 с.
ISBN 978-5-9282-1209-4
Содержит отдельные разделы математики важные для расширенного использования математических методов в профессиональной деятельности.
Пособие подготовлено на кафедре «Математика и математическое моделирование» и предназначено для студентов (квалификация выпускника – магистр) технических вузов, обучающихся по направлению 08.04.01 – «Строительство» с учетом требований Федерального государственного образовательного стандарта поколения «три плюс», а также может быть полезным специалистам и научным работникам, использующим в своей деятельности современные математические методы анализа, моделирования систем и процессов для поиска оптимальных решений и наилучшего способа их реализации.
© Пензенский государственный университет
ISBN 978-5-9282-1209-4 архитектуры и строительства, 2014 © Гарькина И.А., Данилов А.М. 2014
2
«Чем фундаментальнее закономерность, тем проще ее можно сформулировать».
Петр Капица
ПРЕДИСЛОВИЕ
Предлагаемое пособие подготовлено в соответствии с «Федеральным государственным образовательным стандартом высшего образования» по направлению подготовки 08.04.01 Строительство (уровень магистратуры).
При определении содержания исходили из предпосылки, что математика является фундаментом не только математического образования и основой для успешного изучения общетеоретических и специальных дисциплин, но и расширенного использования математических методов в профессиональной деятельности.
С учетом их важности для решения прикладных задач в пособие выборочно включены отдельные вопросы:
–теории вероятностей и математической статистики;
–математической физики;
–временных рядов;
–теории массового обслуживания;
–дискретной математики, логических исчислений, графов.
Пособие может быть полезным специалистам и научным работникам, использующим в своей деятельности современные математические методы анализа, моделирования систем и процессов для поиска оптимальных решений и наилучшего способа их реализации.
При подготовке издания использован собственный практический опыт работы авторов по подготовке магистров, а также по проектированию сложных систем различного назначения.
Авторы выражают свою признательность рецензентам: кафедре «Высшая и прикладная математика» ФГБОУ ВПО «Пензенский государственный университет» (зав. кафедрой – д.ф.-м.н., проф. И.В.Бойков); д.ф.-м.н., проф. О.А.Голованову (Пензенский артиллерийский инженерный институт), сделавшим ряд ценных поправок в процессе подготовки рукописи.
3
ВВЕДЕНИЕ
Дисциплина «М1.Б.3.Специальные разделы высшей математики» входит в базовую часть федерального государственного образовательного стандарта высшего образования по направлению подготовки 08.04.01 «Строительство» (уровень магистратуры).
Процесс изучения дисциплины направлен на формирование ком-
петенций:
–способность использовать углубленные знания правовых и этических норм при оценке последствий своей профессиональной деятельности, при разработке и осуществлении социально значимых проектов (ОПК-7);
–способность и готовность ориентироваться в постановке задачи, применять знания о современных методах исследования, анализировать, синтезировать и критически резюмировать информацию (ОПК-10);
–способность разрабатывать физические и математические (компьютерные) модели явлений и объектов, относящихся к профилю деятельности
(ПК-7).
Цель преподавания дисциплины: обучение современным математическим методам анализа, моделирования процессов и систем для поиска оптимальных решений и наилучшего способа их реализации.
Задачи дисциплины курса состоят в ориентировании студентов на расширенное использование математических методов в профессиональной деятельности.
Врезультате изучения дисциплины магистрант должен:
знать: современные проблемы науки и техники, формы и методы научного познания в применении к профессиональной деятельности;
уметь: формулировать физико-математическую постановку задачи исследований, выбирать и реализовывать методы ведения научных исследований; анализировать и обобщать результаты исследований, доводить их до практической реализации;
владеть: математическим аппаратом для разработки математических моделей процессов и явлений и решения практических задач профессиональной деятельности.
Дисциплина «Специальные разделы высшей математики» опирается на общий курс математики для бакалавров; является одной из основных для изучения дисциплин «Методология научных исследований», «Методы решения научно-технических задач в строительстве», «Философские проблемы науки и техники».
4
1. ТЕОРИЯ ВЕРОЯТНОСТЕЙ
ИМАТЕМАТИЧЕСКАЯ СТАТИСТИКА
1.1.Системы случайных величин
Впрактических задачах часто результат опыта описывается не одной случайной величиной, а системой случайных величин. Случайные ве-
личины X1, X2, , Xn , входящие в систему, могут быть как дискретными,
так и непрерывными.
Пример 1 . Станок-автомат штампует стальные плитки. Если контролируемыми размерами являются длина X и ширина Y , то имеем двумерную случайную величину (X ,Y ); если же контролируется и тол-
щина Z , то имеем трехмерную величину X ,Y , Z .
Двумерную случайную величину (X ,Y ) геометрически можно ис-
толковать как случайную точку или случайный вектор на плоскости XOY . Исчерпывающей характеристикой системы случайных величин является ее закон распределения. Как и для отдельных случайных величин могут быть различные формы задания системы случайных величин (функция распределения, плотность распределения, таблица вероятностей
отдельных значений случайного вектора и т.д.).
Если рассматривается двумерная дискретная случайная величина (X ,Y ) , то ее двумерное распределение можно представить в виде таблицы
(матрицы) распределения:
|
|
|
|
|
|
|
n |
X |
x1 |
x2 |
… |
xi |
… |
xn |
|
|
|
|
|
|
|
|
i 1 |
y1 |
p11 |
p21 |
… |
pi1 |
… |
pn1 |
p1 |
… |
… |
… |
… |
… |
… |
… |
… |
yj |
p1j |
p2j |
… |
pij |
… |
pnj |
pj |
… |
… |
… |
… |
… |
… |
… |
… |
ym |
p1m |
p2m |
… |
pim |
… |
pnm |
pm |
n |
|
|
|
|
|
|
|
|
p1 |
p2 |
… |
p1pi |
… |
pn |
1 |
j 1 |
|
|
|
|
|
|
|
где x1 x2 |
xn , y1 y2 |
ym , pij |
– вероятность события, заключаю- |
щегося в |
одновременном |
выполнении |
равенств X xi ,Y y j . При этом |
n m
pi j 1. Таблица может содержать бесконечное множество строк и
i 1 j 1
столбцов.
5

Пример |
2 . Двумерная дискретная величина X ,Y |
задана законом |
|||
распределения: |
|
|
|
|
|
|
|
|
|
|
|
X |
Y |
2 |
3 |
|
4 |
|
|
|
|
|
|
2 |
|
0,3 |
0,15 |
|
0,05 |
3 |
|
0,15 |
0,10 |
|
0,05 |
4 |
|
0,05 |
0,05 |
|
0,05 |
5 |
|
0,05 |
0 |
|
0 |
Найти законы распределения составляющих X и Y .
Решение. Сложив вероятности по столбцам, получим вероятности возможных значений X , то есть:
P X xi pi ;
P X 2 0,3 0,15 0,05 0,05 0,55;
P X 3 0,15 0,10 0,05 0 0,3;
P X 4 0,05 0,05 0,05 0 0,15;
0,55 0,3 0,15 1.
Сложив вероятности по строкам, получим вероятности возможных значений Y :
P Y y j p j ;
P Y 2 0,3 0,15 0,05 0,50;
P Y 3 0,15 0,10 0,05 0,30 ;
P Y 4 0,05 0,05 0,05 0,15;
P Y 5 0,05 0 0 0,05;
0,50 0,30 0,15 0,05 1.
Законы распределения X и Y имеют вид:
xi |
2 |
3 |
4 |
pi |
0,55 |
0,3 |
0,05 |
6
|
y j |
|
2 |
3 |
|
4 |
|
|
5 |
|
|
|
pj |
|
0,5 |
0,3 |
|
0,15 |
|
0,05 |
|
|
|
Функцией |
распределения |
двух |
случайных величин X ,Y называется |
||||||||
вероятность совместного выполнения двух неравенств X x, Y y : |
|||||||||||
|
F x, y P X x,Y y . |
|
|
|
|
||||||
Пример 3. Задана функция распределения двумерной случайной |
|||||||||||
величины X ,Y |
|
|
|
|
|
|
|
|
|
||
|
F x, y 1 e x 1 e y |
x 0, y 0 . |
|||||||||
Найти вероятность того, что в результате испытания составляющие X |
|||||||||||
и Y примут значения соответственно X 2,Y 4. |
|
|
|
|
|||||||
Решение. P X 2,Y 4 |
F 2,4 1 e 2 1 e 4 0,849 . |
||||||||||
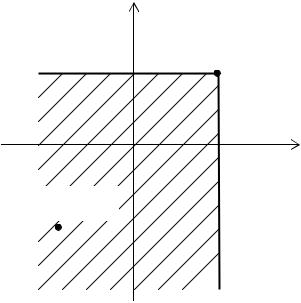
Геометрически F x, y |
есть |
вероятность того, |
что |
|
случайная точка |
||||||
X ,Y попадет в бесконечный квадрант с вершиной |
x, y |
, расположенный |
|||||||||
левее и ниже этой точки. Правая и верхняя границы области в квадрант не включаются (рис. 1.1).
Y
(x, y)
X
(X, Y)
Рис. 1.1
В случае дискретной двумерной случайной величины ее функция
распределения определяется по формуле
F x, y pi j ,
i j
где суммирование вероятностей распространяется на все i , для которых xi x , и все j , для которых y j y .
7
Укажем основные свойства функции распределения.
1. Функция распределения F x, y есть неотрицательная функция, заключенная между нулем и единицей:
0 F x, y 1 (следует из определения F x, y как вероятности).
2. |
Функция распределения F x, y |
есть неубывающая функция по |
|
каждому из аргументов: |
F x2, y F |
x1, y ; |
|
|
при x2 x1 |
||
|
при y2 y1 |
F x, y2 F |
x, y1 . |
Действительно, пусть x2 x1 . Тогда, используя аксиому сложения вероятностей для несовместных событий, получим:
F x2, y P X x2,Y y P X x1,Y y + P x1 X x2,Y y P X x1,Y y = F x1, y .
Аналогично, при y2 y1 получили бы F |
x, y2 F x, y1 . |
3. При одном из аргументов, равным |
, функция распределения |
системы превращается в функцию распределения случайной величины, соответствующей другому аргументу:
|
|
|
F x, F1 x P X x ; |
|
|
|
|
|
|
F , y F2 y P Y y , |
|
|
|
где F1 x , F2 y – |
функции распределения случайных величин |
X и Y |
||||
|
|
|
соответственно. |
|
|
|
Действительно, |
F x, P |
X x,Y P X x F1 |
x , так как |
|||
любое событие |
|
X x , будучи |
умноженным на достоверное |
событие |
||
|
|
|
|
|
|
|
Y , не меняется. Аналогично получили бы F , y F2 y .
4. Если оба аргумента равны , то функция распределения равна единице:
F , 1
(совместное осуществление достоверных событий X и Y
есть событие достоверное).
5. Если хотя бы один из аргументов равен , то функция распределения равна нулю:
F x, F , y F , 0
8
(так как события |
|
X , |
Y и их произведение являются |
|
|
|
невозможными событиями).
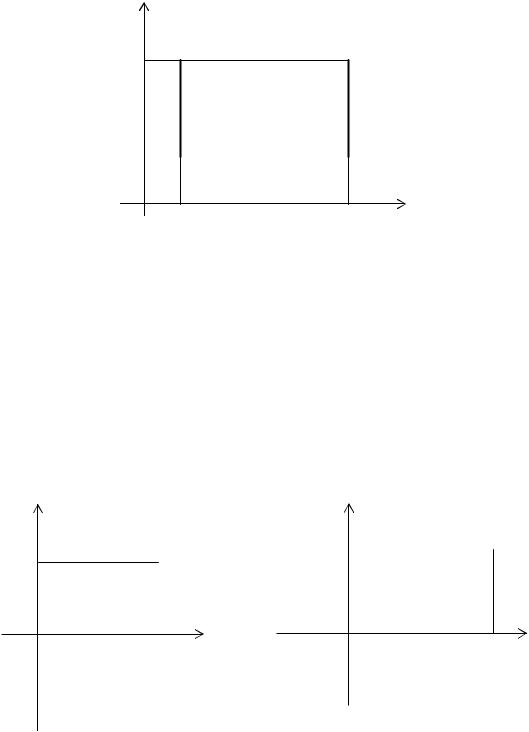
6.Вероятность попадания значений двумерной случайной величины
X ,Y в прямоугольник ABCD (рис. 1.2) можно найти с помощью ее
функции распределения F x, y по формуле
P a X b,c Y d F b,d F a,d F b,c F a,c . |
|||||
|
|
|
|
|
|
y |
|
|
|
|
|
d |
A |
|
B |
|
|
|
|
|
|
|
|
c |
|
|
|
C |
D |
|
|
||
|
|
|
||
|
a |
b |
x |
|
|
|
Рис. 1.2 |
|
|
Эта формула получается из двух формул для вероятности попадания значений X ,Y в вертикальную или горизонтальную полуполосу.
Вероятность того, что значения величины X ,Y попадут в полуполосу a X b,Y y (рис.1.3) выражается формулой
|
P a X b,Y y F b, y F a, y . |
|
|
||
Вероятность того, что значения величины X ,Y попадут в полуполосу |
|||||
X x,c Y d (рис.1.4) выражается формулой |
|
|
|||
|
P X x,c Y d F x,d F x,c . |
|
|
||
y |
|
|
y |
|
|
y |
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
a |
|
b x |
x |
x |
|
|
|
|
|
|
|
Рис. 1.3 |
Рис. 1.4 |
9

Таким образом, вероятность попадания двумерной случайной величины в полуполосу равна приращению функции распределения по одному из аргументов.
Двумерная случайная величина X ,Y называется непрерывной, если ее
функция распределения F x, y – непрерывная функция, дифференцируемая по каждому из аргументов, у которой существует вторая
смешанная производная 2F x, y .
Обе составляющие X и Y представляют собой непрерывные случайные величины.
Вводя в рассмотрение плотность распределения непрерывной случайной величины X , ее определяли как предел отношения вероятности попадания на малый участок к длине этого участка при ее неограниченном уменьшении. Аналогично плотность распределения системы двух случайных величин X ,Y определяется как предел отношения вероят-
ности попадания случайной точки X ,Y в малый прямоугольник D к
площади этого прямоугольника, когда оба его размера стремятся к нулю.
Найдем предел отношения вероятности попадания случайной точки
X ,Y в элементарный прямоугольник
x X x x; y Y y y
к площади этого прямоугольника x y , когда x и y 0. Полагая a x, c y , b x x, d y y , получим:
P x X x x, y Y y y
F x x, y y F x, y y F x x, y F x, y .
Тогда, если F x, y не только непрерывна, но и дифференцируема, получим:
lim P x X x x, y Y y yx 0 x y
y 0
= lim
x 0y 0
F x x, y y F x, y y |
F x x, y F x, y |
|||
|
|
|
|
= |
|
x y |
|
|
|
|
|
|
|
|
lim |
1 |
F |
x x, y y |
F x, y y |
|
|||||||
|
lim |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
x |
|
|
|||||
y 0 |
y x 0 |
|
|
|
|
|
|
|
||||
lim |
F x x, y F x, y |
|
|
2F x, y |
f x, y . |
|||||||
|
|
|
|
|
|
|
|
|
||||
|
|
x |
|
|
|
xdy |
||||||
x 0 |
|
|
|
|
|
|
|
|
|
|||
10
