Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

971

.pdf

Скачиваний:

Добавлен:

17.06.2024

Размер:

1 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 148 9 10 11 12 13 14 > Следующая >>>

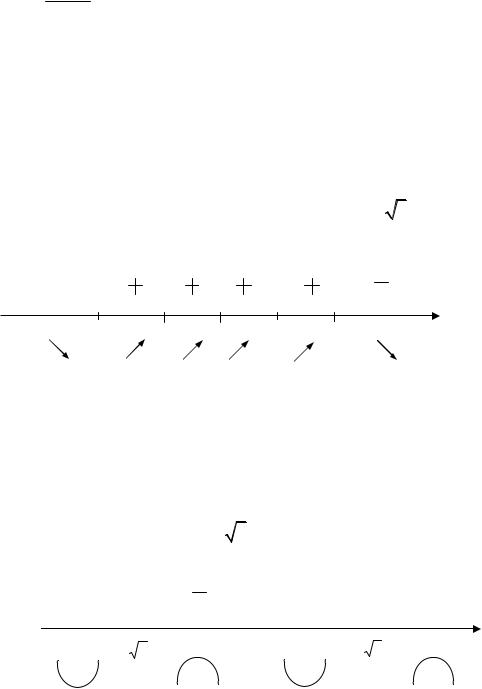
3. Симметрия. Периодичность.

f x	x3	f x (нечетная функция). График симметричен от-
	3 x2

носительно начала координат.

4. Точки пересечения графика с осями.

x 0, y 0 – пересечение с осями координат. 5.Точки экстремума. Интервалы монотонности.

3 x

2x x

0 ; 9x2 x4

3 x2 2

x2 9 x2 0;

x 0,

x 3 , x 3 .

Рис. 2.17

ymin

9 ;

ymax 3

9 .

3 9

6.Точки перегиба. Интервалы выпуклости и вогнутости.

6x 9 x2

0, x 0 , x 3 .

3 x2 3

Рис. 2.18

(0;0) – точка перегиба (перегиб с на ). 7. График функции.

4,5

3 0

3 3

- 4,5

Рис. 2.19

3.ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

3.1. Функция нескольких переменных. Область определения

Переменные x, y называют независимыми, если каждая из них может

принимать любые значения независимо от того, какие значения принимает другая.

Если каждой паре значений независимых x и y из некоторой области

их изменения D соответствует определенное значение величины Z , то Z есть функция двух независимых переменных x, y , определенная в об-

ласти D .

Обозначение: z f x; y

Пример 1. Объем кругового цилиндра есть функция от радиуса R его основания и от высоты H , зависимость между этими переменными дается

формулой: V R2H .

Решение. Совокупность пар значений x, y , при которых определяется функция z f (x, y) , называется областью определения D этой функции.

y	Каждой паре значений	(x; y) соот-
	ветствует точка плоскости	xOy и D яв-

3ляется плоской областью в плоскости xOy .

3	Пример 2. найти область определе-
0	x	9 x2 y2 .
	ния функции z	9 x2 y2 .
	Решение. Функция определена для
	значений x, y , удовлетворяющих нера-
Рис. 3.1	венству 9 x2 y2	0 или x2 y2 9 .
Рис. 3.1	Это означает, что функция определе-
	Это означает, что функция определе-

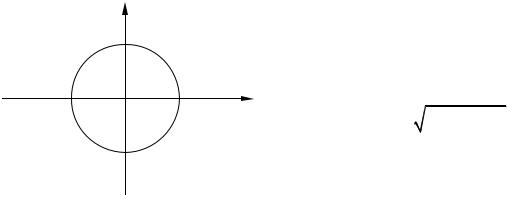
на в точках, лежащих внутри окружности x2 y2 9 и на ее границе (рис. 3.1). Такую область определения на-

зывают замкнутой.

Пример 3. Найти область определения функции z ln 9 x2 y2 . Решение. Функция определена лишь для тех x, y , которые удовлетво-

ряют неравенству: 9 x2 y2 0 или x2 y2 9 .

Геометрически область определения представляет собой внутренность круга (рис. 3.2).

Рис. 3.2

Если совокупности значений независимых переменных (х1, х2, …, хn), взятых из некоторой области, соответствует определенное значение переменной W, то говорят, что W является функцией n независимых переменных х1, х2, …, хn и пишут W = f(х1, х2, …, хn); так же как для функции двух переменных вводится понятие области определения функции любого числа переменных.

Для функции трех переменных область определения есть совокупность троек чисел (x, y, z). Каждой тройке чисел соответствует некоторая точка пространства и область определения функции трех переменных есть некоторая пространственная область.

Пример 4. Объем V усеченного конуса является функцией от трех независимых переменных – радиусов R и r обоих его оснований и высот Н.

Решение. V 13 H R2 Rr r2 . Изучая физическое состояние какого-

нибудь тела, наблюдают изменение его свойств от точки к точке (например плотность, температура тела). Эти величины – функции координат (x, y, z) точки – функции трех переменных. Если физическое состояние тела меняется во времени, то к этим независимым переменным присоединяется еще и время t. Получаем функцию четырех независимых переменных

3.2. Частные производные. Дифференциалы

Если приращение функции z f (x, y) получено за счет приращения не-

зависимой переменной х при неизменном значении другой независимой переменной у, то приращениефункции Z называетсячастным приращением функ-

ции z f (x, y) попеременной x иобозначается: x z f (x x, y) f (x, y)

Аналогично вводится понятие частного приращения функции по пере-

менной у: y z f (x, y y) f (x, y) .

Полным называется приращение функции, получаемое за счет приращения обеих независимых переменных х, у и обозначаемое

z f (x x, y y) f (x, y).

Частной производной по х от функции z f (x, y) называется предел отношения x z к приращению x при стремлении x к нулю.

z	lim	x z	lim	f (x x, y) f (x, y)	,
x				x
	x 0	x	x 0

обозначаемый одним из символов: zx , fx (x, y), xz , fx . Аналогично определяется частная производная по у:

lim

y z

lim

f (x, y y) f (x, y)

y 0

обозначаемый z

f (x, y),

Частная производная по х вычисляется в предложении, что у – постоянная; частная производная по у вычисляется в предложении, что х – постоянная. Правила вычисления частных производных совпадают с правилами дифференцирования функции одного переменного.

Пример 1. Найти частные производные функции z 5x4 6x2 y3 y5 . Решение. Полагая у постоянной, находим

zx (5x4 6x2 y3 y5 )x 20x3 12xy3

(производная по х от у5 равна нулю, как производная от постоянной).

При отыскании zy переменная х рассматривается как величина посто-

янная, а потому

zy 18x2 y2 5y4 .

Пример 2. Найти частные производные функции z xy5 .
Решение. Полагая при определении zx		величину у постоянной, полу-
чим, что z – есть степенная функция: z y5 xy5 1
	x
При нахождении zy , полагая х постоянной, получим, что z является по-
казательной z	xy5 ln x ( y5 ) 5y4 xy5 ln x .
y	y
Пример 3.	Показать, что функция z x3		7x2 y 3y3	удовлетворяет
уравнению xzx	yzy 3z .
Решение. Найдем частные производные		z	3x2 14xy ;	z 7x2 9 y2 .
		x		y

Затем первую из них умножим на х, вторую – на у и результаты сложим:

x(3x2 14xy) y(7x2 9 y2 ) 3(x3 7x2 y 3y3 ) 3z ,

что и требовалось доказать.

Пример 4. Вычислить частные производные функции

z ln(x2 4 y5 ) в точке x 2, y 1.	z	2x	,	z	20 y4	.
	x	x2 4 y5		y	x2 4 y5

Решение. Полагая x 2, y 1, вычисляем значение производных в указанной точке

zx (2,1) 0.5, zy (2,1) 2,5.

Частные производные функции любого числа переменных определяются аналогично. Так, если z f (x1, x2 ,..., xn ) , то

lim

x1z

;

lim

x2 z

и так далее.

x1 0

x2 0

Пример 5. Найти частные производные функции U

y2 z2

Решение. Частные производные имеют вид:

(x2

y2 z2 ) x(x2 y2 z2 )

y2 z2 x2

(x2 y2 z2 )2

(x2 y2 z

2 )2

2xy

;

(x2 y2 z2 )2

2xy

(x2 y2 z2 )2

3.3. Частные производные высших порядков.

Если задана функция z f (x, y) , то ее частные производные zx и zy

также являются функциями независимых переменных х и у и от каждой из них можно вычислить производные по х и у.

Частной производной второго порядка функции z f (x, y) называется частная производная от частной производной первого порядка.

Каждую из частных производных первого порядка можно продифференцировать по каждой из двух независимых переменных и функция двух переменных имеет четыре частные производные второго порядка. Они обозначаются:

z	=	2 z		f (x, y) (f дифференцируетсяпоследовательнодваразапох);
		x2
xx					xx
z	=	2 z			f (x, y)	(f дифференцируется по у, а потом результат диф-

xy		x y			xy

ференцируется по х);
z	=	2 z			f (x, y)	(f дифференцируется сначала по х, а потом ре-

xy		y x			yx

зультат дифференцируется по у);
z		2 z			f (x, y)	(f дифференцируетсяпоследовательнодваразапоу).
yy		y	2		yy

Производные второго порядка можно снова дифференцировать как по х, так и по у. Получим частные производные более высокого порядка.

Частная производная высшего порядка, взятая по различным переменным, называется смешанной частной производной.

	2 f			2 f	( f	f ) .
					( f	f ) .
	x y			y x	xy		yx
	x y			y x
Если функция z f (x, y)		и ее частные производные						f , f , f		, f	опре-
								x	y xy	yx
делены и непрерывны в точке М (х, у) и ее окрестности, то
z		z			( f		f ),
	xy		yx		xy		yx

т.е. результат дифференцирования функции нескольких переменных не зависят от порядка дифференцирования.

Пример 6. Найти частные производные второго порядка функции z x4 8x2 y3 .

Решение. Сначала находим частные производные первого порядка

z	4x3 16xy3, z	24x2 y2 .
x	y

Затем искомые частные производные

z	12x2 16 y3, z	z	48xy2 , z	48x2 y .
xx	xy	yx	yy

Пример 7. z xln(xy) . Показать, чтоx2 z yz .

Решение. Найдем:

ln(xy)

(xy)

ln(xy) 1,

z x

(xy)

ln(xy) 1

y 1 .

Левая и правая части данного равенства равны

2 2 z

x, y

и данное равенство справедливо.

3.4.Дифференциал функции двух переменных

иего приложение для приближенных вычислений

Полным дифференциалом функции z f (x, y) называется главная часть ее полного приращения линейная относительно приращений x, y

(или, что то же, дифференциалов dx,dy ). Полный дифференциал функции z f (x, y) обозначается символом dz и вычисляется по формуле

dz zx dx zydy

При достаточно малых приращениях аргументов полное приращение функции можно с малой относительной погрешностью заменять ее полным дифференциалом, т.е.

z zxdx zydy ,			откуда		f (x x, y y) f (x, y) zxdx zydy .
Это приближенное равенство тем точнее, чем меньше величины dx,dy .
Пример 8.		Вычислить приближенно (0,98)3,05 .
Решение.		Рассмотрим		функцию		вида	z xy .	В точке (1;3)
(x 1; y 3)	z 1.
Положим x 0,02 и y 005 (попадаем в точку x 0,98и y 3,05 ).
Тогда
(0,98)3,05 13 f x f y						f	yxy 1; f	xy ln x
			x		y	x	y
и в точке (1;3)		f 313 1; f		13 ln1 0 и		(0,98)3,05 1 3 ( 0,02) 0,94.
		x	( y)

3.5. Производная по направлению. Градиент

Предел

lim

f (M ) f (M0 )

если он существует, называется производ-

M M0

ной функции f в точке М0 по направлению вектора l M0M и обозначает-

ся

. Если функция f дифференцируема в точке М0, то

cos .

cos

z M0

Вектор

gradf

называется градиентом функции f (М) в точке М0.

Производная в данной точке по направлению вектора l

имеет наи-

большее значение, если направление вектора l

совпадает с направлением

градиента; это наибольшее значение производной равно

gradf

Пример .9. Найти gradz функции z x2

xy в точке A( 2;3) .

Решение. Найдем градиент в произвольной точке

grad z

(2x

y)i

x j .

Значение градиента в точке A( 2,3) grad z A i 2 j .

Пример 10.

Найти производную по направлению вектора

2i 3 j в

точке A (2;3) от функции Z x2 y xy3 .

Решение.

Найдем cos

; cos

(2xy y3 )

15 ;

(x2

3xy2 )

50 .

x 2

y 3

Получим:

A 15

180

13 .

3.6. Экстремум функции двух независимых переменных

Точка М0 (х0 , у0 ) называется точкой локального максимума (миниму-

ма), если для всех точек М из некоторой окрестности точки М0 и отлич-

ных от неё выполняется неравенство f (M )

f (M0 ) , f (M ) f (M0 ) .

Если функция Z

f x; y

достигает экстремума в точке М0 (х0 , у0 ) ,

то каждая частная производная первого порядка от Z или обращается в

нуль в этой точке, или не существует.

0 ,

0 . (Необхо-

димое условие экстремума).

dx M0

dy M0

Точки, удовлетворяющие ему, называются критическими.

Обозначим: А d

;

; C d

dxdy

Если в некоторой окрестности критической точки М0 (х0 , у0 ) , функция Z f x, y имеет непрерывные частные производные до третьего порядка включительно, то в точке М0 (х0 , у0 )

а) f (x, y) имеет максимум, если AC B2 0 и A 0 ; б) f (x, y) имеет минимум, если AC B2 0 и A 0;

в) f (x, y) не имеет экстремума, если AC B2 0 .

(Достаточное условие экстремума)

Если AC B2 0 , то признак не даёт ответа на вопрос о существовании экстремума в точке М0 .

Пример 11. Найти точки экстремума функции z x2 y2 2 y 1

Решение. Найдём критические точки функции:		dz	2x ,	dz	2 y 2 .
		dx		dy
Из условия zx 0 ,	2x 0
Из условия zx 0 ,	zy 0 получим систему	0
	2 y 2	0
Решение: x 0,	y 1. Следовательно, критическая точка M0 (0;1) .

С помощью достаточного признака исследуем найденную критическую точку M0 (0;1) . Дляэтогонайдемчастныепроизводныевторогопорядка:

A	d 2 z	2, B	d 2 z		0, C	d 2 z	2 .

	dx2		dxdy			dy2
		м		м			м
Таким образом	AC B2 4 0; A 2 0 .
Следовательно, точка M0 (0;1)			является точкой минимума функции.

<<< < Предыдущая 1 2 3 4 5 6 78 / 148 9 10 11 12 13 14 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.06.2024993.41 Кб0967.pdf
#
17.06.2024993.9 Кб0968.pdf
#
17.06.2024999.51 Кб1969.pdf
#
16.06.2024187.07 Кб097.pdf
#
17.06.2024999.72 Кб0970.pdf
#
17.06.20241 Mб0971.pdf
#
17.06.20241 Mб0972.pdf
#
17.06.20241 Mб0973.pdf
#
17.06.20241.01 Mб0974.pdf
#
17.06.20241.01 Mб5975.pdf
#
17.06.20241.01 Mб0976.pdf