Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2351

.pdf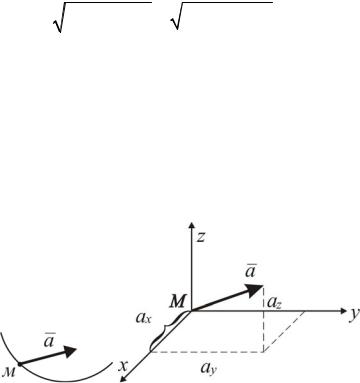

Скачиваний:

Добавлен:

17.06.2024

Размер:

7.52 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 228 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

С учетом выражения (2.1.10) уравнение (2.1.4) можно представить в виде

v dr	dx		dy		dz		.	(2.1.12)
		i		j		k
dt	dt		dt		dt

Сопоставляя уравнения (2.1.12) и (2.1.11), получаем:

vx	dx
vx	dt	x;
	dt
	dy
vy	dy		(2.1.13)
vy	dt	y;	(2.1.13)
	dt
vz	dz
vz	dt	z.
	dt

Проекция скорости на координатную ось равна первой производной от соответствующей координаты по времени.

Полная величина скорости

vx2 vy2 vz2

x2 y2 z2 .

(2.1.14)

Направление вектора скорости определяем с помощью направляющих косинусов:

cos(v ,

; cos(v ,

(2.1.15)

Вектор ускорения точки также можно записать через проекции:

a ax		ay		az		,	(2.1.16)
	i		j		k

Рис. 2.5. Ускорение точки и его проекции

С другой стороны, дифференцируя уравнение (2.1.12) по времени, получаем:

d 2 x

d 2 y

d 2 z

k .

(2.1.17)

Сопоставляя выражения (2.1.17) и (2.1.16), записываем:

ax dvx			d		2	x
								;
	dt			dt2
ay	dvy			d 2 y
						2		;	(2.1.18)
	dt			dt

az	dv	z		d 2 z
				dt2			.
	dt

Проекция ускорения на какую-либо ось равна второй производной от соответствующей координаты по времени.

Величина ускорения точки М определяется из выражения

ax2 ay2 az2.

(2.1.19)

Направление вектора ускорения определяем с помощью направляющих косинусов:

cos(a,

; cos(a,

(2.1.20)

Пример . Уравнения движения точки имеют вид: x 10sin 3 t, см,

y 5cos 3 t, см.

Найти траекторию точки, v и a в момент времени t1= 1 c.

Решение.

Возведя обе части каждого уравнения в квадрат и сложив полученные уравнения, имеем:

x2 y2 1. 102 52

Такимобразом, уравнениетраекторииточки– эллипс(рис. 2.6).

При t1=1 с x1=8,66 см, y1=2,5 см.

Проекции скорости:

vx dx		10	cos			t 5,233 см/с,
	dt		3			3
	dy
vy		5			sin
	dt			3		3	t 4,532 см/с.

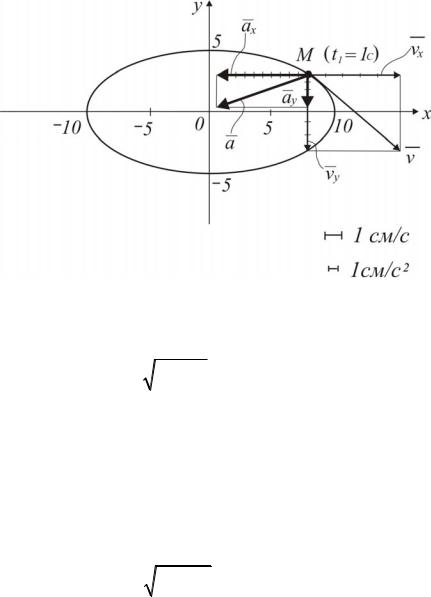
Рис. 2.6. Траектория движения и кинематические характеристики движения точки в момент времени t1=1 с

Величина скорости точки М:
	v			vx2		vy2		6,922 см/с.
Проекции ускорения:						2
ах dvx 10						2	sin		t 9,487 см/с2		;
	dt					9			3
ау	dv	y	5		2		cos			t 2,738 см/с2 .
ау			5			9	cos		3	t 2,738 см/с2 .
	dt					9			3
Величина ускорения точки:
	a			ax2		ay2		9,87 см/с2 .

2.2. Определение скорости и ускорения точки при естественном способе задания движения

2.2.1. Естественный способ задания движения точки

Если известна траектория точки, то удобно движение задавать в следующем виде. Будем отсчитывать расстояния s от некоторой точки траектории О до движущейся точки М:

s=s(t).

(2.2.1)

Здесь s – дуговая координата точки;

s(t) – дважды дифференцируемая непрерывная функция от времени.

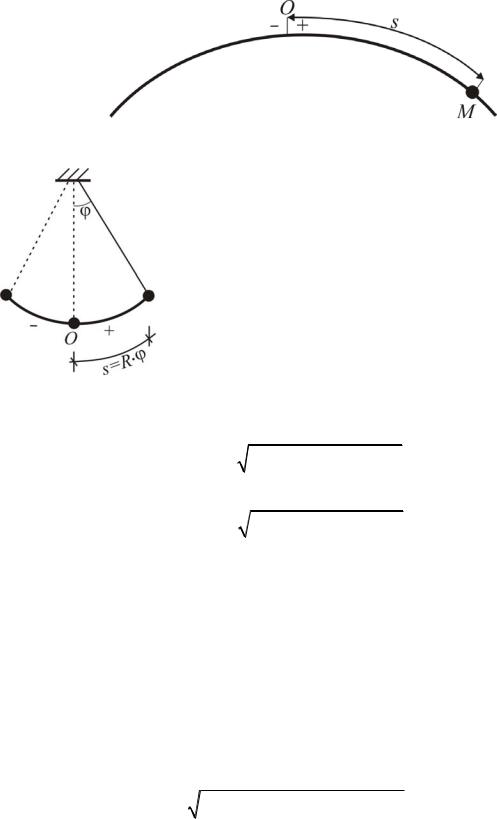
Рис. 2.7. Естественный способ задания движения точки

Рис. 2.8. Дуговая координата точки не равна ее пути

тогда

Так как

значит,

Расстояние s в одну сторону от точки О считается положительным, в другую – отрицательным. Точку О удобно брать в том месте траектории движения, где точка находится в начальный момент времени. Расстояние s=ОМ может быть не равно пути, пройденному точкой. Например, при колебаниях маятника дуговая координата многократно равна 0, в то время как путь, пройденный точкой, непрерывно увеличивается.

Траектория движения может быть задана или уравнениями, или словесно, или в виде графика. Между заданиями движения в декартовой и естест-

венной формах легко установить связь. Как известно, дифференциалдугикривой

ds	(dx)2		(dу)2 (dz)2 ,	(2.2.2)
t
s	(dx)2		(dу)2 (dz)2 .	(2.2.3)
0
	x f		(t),
		1		(2.2.4)
	у f2 (t),			(2.2.4)
	z
	z	f3 (t),
	dx
	dx	f1(t)dt,
	dу			(2.2.5)
	dу	f2 (t)dt,		(2.2.5)
	dz
	dz	f3 (t)dt,

t		2		(t))	2		2	dt .
s									(2.2.6)
	( f1(t))		( f2			( f3 (t))
0

2.2.2. Скорость точки при естественном способе задания движения

Пусть известны траектории точки и закон движения точки по траектории s=s(t). Определим скорость точки.

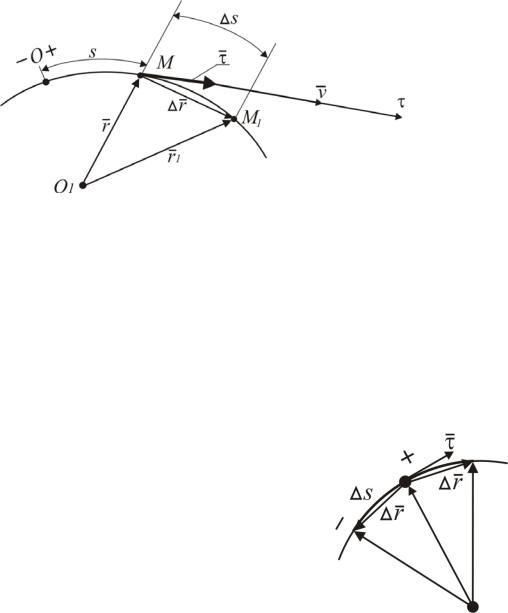
Пусть в момент времени t точка занимает положение М, а в момент времени t1 t t – положение М1 (рис. 2.10). Проведем из неподвижной точки О1

радиусы-векторы r и r1 , определяющие положение точки в моменты времени t иt1 Какбылоустановленоранее,

v dr .	(2.2.7)
dt

Рис. 2.10. Скорость точки при естественном способе задания движения

Перепишем уравнение (2.2.7) в виде
v dr ds .
Тогда		ds		dt
Тогда
dr	lim			r	.
ds		s 0		s
При s 0			1.
			1.
Направление вектора не зависит от знака со-

отношения	r	. На самом деле, при s 0 знак от-
	s		r	r
ношения отрицательный, то есть			r	r	(рис.
			s	s

(2.2.7’)

(2.2.8)

(2.2.9)

2.11). При этом вектор			направлен положительно.
При s 0 r	r	и	опять направлен в поло-
	s
s				Рис. 2.11. Направление
жительном направлении.			Значит, единичный вектор
всегда направлен по касательной к траектории в сто-				вектора

ронувозрастающих(положительных) расстоянийдуговойкоординаты.

Итак,
		v ds	.	(2.2.10)
		dt
При	ds	0 вектор скорости точки v	направлен в сторону возрастаю-
	dt

щих расстояний дуговой координаты.

При dsdt 0 вектор скорости точки v направлен в сторону убывающих

расстояний дуговой координаты. Величину

v ds	(2.2.10)
dt

называют алгебраической скоростью точки или проекцией скорости на касательную ось. Касательная ось направлена так же, как и (единичный вектор).

2.2.3. Элементы геометрии кривой

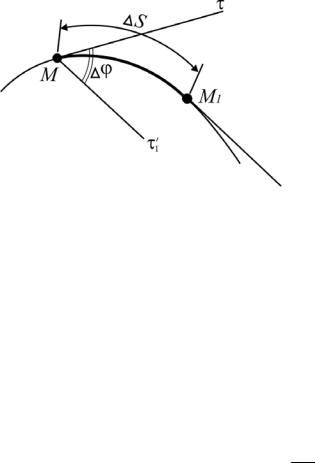
Пусть в моменты времени t и (t+ t) точка занимает на траектории соответственно положения М и М1. При этом касательные оси и 1 – соответственно (рис. 2.11). Расстояние междуточкамиМиМ1 равно s.

В общем случае пространственной кривой касательные М и М1 1 скре-

щиваются. Угол между М и M 1 на-

Рис. 2.11. Угол смежности зывают углом смежности. Кривизной кривой в точке М называют предел от-

ношения угла смежности к расстоянию s			при стремлении s к нулю:
k lim		d .		(2.2.11)
s 0	s		ds

Радиусом кривизны в точке М называют величину, обратную кривизне:

1	ds	.	(2.2.12)
k
	d

Для окружности радиус кривизны совпадает с радиусом окружности. В самом деле, для окружности

s R , ds R d R . d d

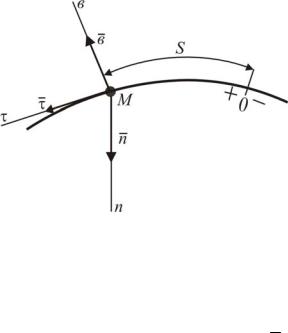
2.2.4. Естественные оси

Проведем через М и M '		(рис.	2.11) плоскость. При стремлении
	1
s 0,	М1 М плоскость займет некоторое предельное положение –
положение соприкасающейся плоско-
сти, т.е. соприкасающаяся плоскость
пройдет через касательные к кривой в
двух соседних точках.
Проведем (рис.2.12) в соприка-
сающейся плоскости из точки М ось
n . Эту ось направим в сторону во-
гнутости траектории. Ось n назы-
вается главной нормалью. Перпенди-
кулярно к соприкасающейся плос-			Рис. 2.12. Естественные оси
кости проведем ось b в ту сторону,
глядя откуда ближайшее совмещение

с n будет казаться направленным против хода часовой стрелки. Ось b называют бинормаль. Итак, оси , n, b называются естественными осями кривой. При движении точки по кривой собственный трехгранник движется

вместе с точкой, поворачиваясь вокруг нее. Единичные векторы , n и b , направленные вдоль осей , n и b, называются единичными ортами.

2.2.5. Дифференцирование единичного вектора

Вычислим производную единичного вектора по скалярному аргумен-

ту	d	.
ту		.
	dt
	Известно, что
				1.			(2.2.13)
	Тогда
		d	d			0	(2.2.14)
		dt			dt
или
		2d 0 .					(2.2.15)
			dt
	Но оба сомножителя здесь не равны нулю:
		0,		d	0		d	.
		0,			0			.
				dt			dt

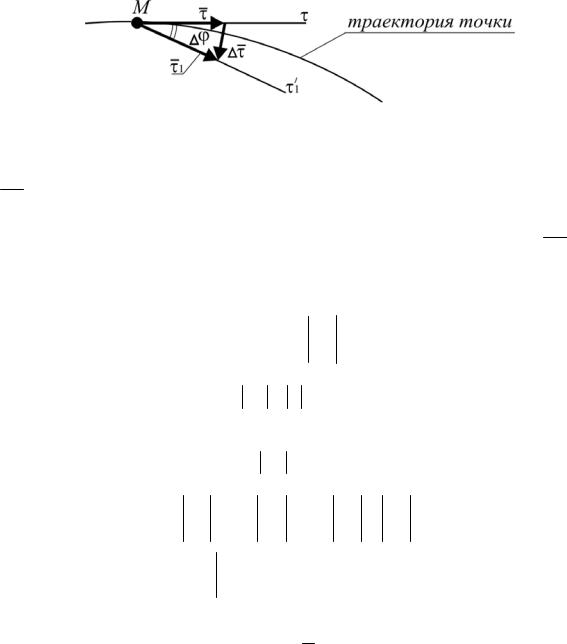
Рис. 2.13. Направление

Так как в пределе лежит в соприкасающейся плоскости, то вектор ddt находится в соприкасающейся плоскости, он перпендикулярен вектору

и направлен в сторону вогнутости траектории; следовательно, ddt на-

правлен также, как n . Можно записать:

или

d dt

d d n . dt dt

sin

1 ,

lim lim d ,

t t dt

d v n . dt

(2.2.16)

(2.2.17)

(2.2.18)

2.2.6. Ускорение точек при естественной форме задания движения

Дифференцируя выражение для скорости v dsdt , получим:

d 2s

(2.2.19)

dt2

Касательная составляющая ускорения

a dv ,

(2.2.20)

нормальная составляющая ускорения an v2 n,

полное ускорение

a a an.

Проекция ускорения на касательную ось a dvdt ,

проекция ускорения на нормальную ось an v2 ,

проекция ускорения на бинормаль равна нулю: ab 0 .

Величина ускорения

a (a )2 (an )2 .

(2.2.21)

(2.2.22)

(2.2.23)

(2.2.24)

(2.2.25)

(2.2.26)

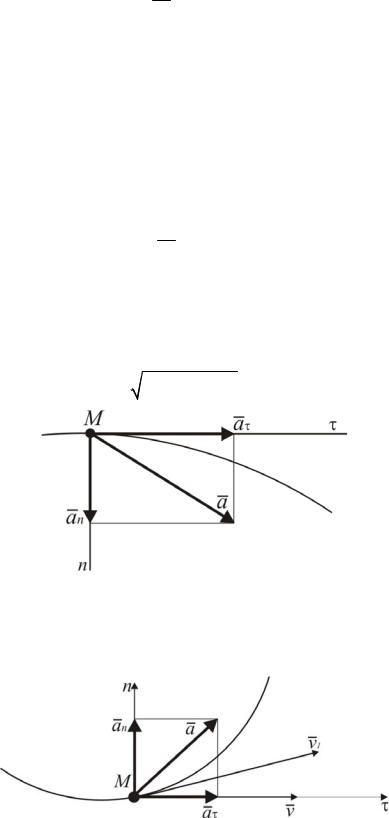
Рис. 2.14. Разложение ускорения на нормальную и касательную составляющие

В самом деле, соприкасающаяся плоскость n проведена через векторы скорости двух соседних точек.

Рис. 2.15. Ускорение лежит в соприкасающейся плоскости

Вектор ускорения

a dv	lim	v	lim v1 v	,
dt		t	t

как v1 и v , лежит в соприкасающейсяплоскости. Следовательно, ускорениене можетпроектироватьсянаосьb. Значит, ab 0.

Итак,

	dv	,
a	dt	,
	dt
	v2
	v2
an		,
an		,

ab 0.

Если

если

a a2 an2 .

s 0, s 0

– ускоренное движение;

s 0, s 0

– замедленное движение.

s 0, s 0

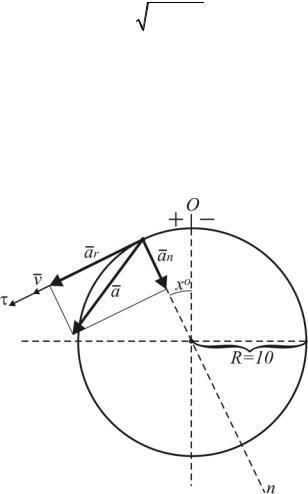
Пример . Точка движется по окружности R=10 см по закону s 4t2 см. Определить скорость и ускорение точки в момент времени t 1 c.

Рис. 2.16. Положение точки на траектории и ее скорость и ускорение в данный момент времени

Положение точки на траектории определим из следующих соображений:

s 4t2 4 см,

<<< < Предыдущая 1 2 3 4 5 6 78 / 228 9 10 11 12 13 14 15 16 17 18 19 20 21 22 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
17.06.20247.45 Mб02347.pdf
#
17.06.20247.46 Mб02348.pdf
#
17.06.20247.47 Mб12349.pdf
#
17.06.2024243.26 Кб0235.pdf
#
17.06.20247.49 Mб02350.pdf
#
17.06.20247.52 Mб02351.pdf
#
17.06.20247.53 Mб02352.pdf
#
17.06.20247.56 Mб02353.pdf
#
17.06.20247.61 Mб02354.pdf
#
17.06.20247.64 Mб72355.pdf
#
17.06.20247.64 Mб02356.pdf