
2351
.pdf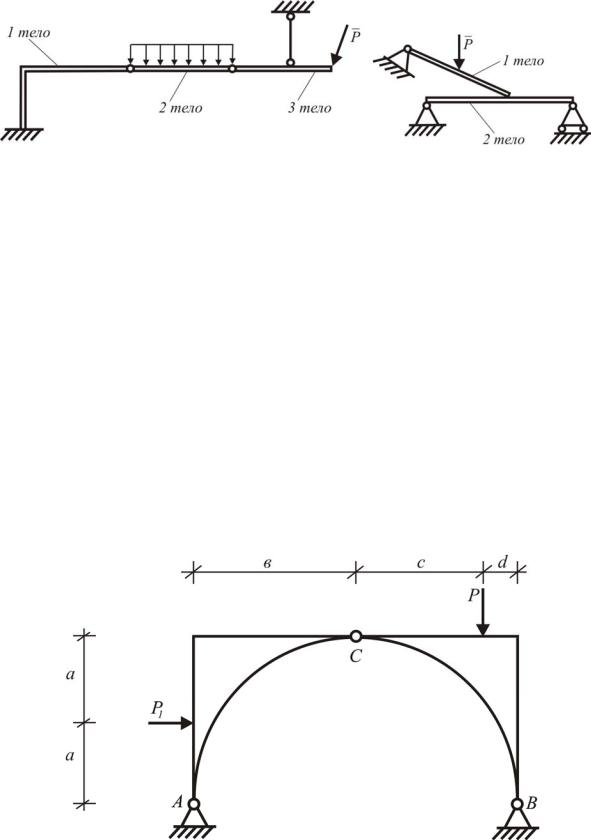
Рис. 1.42. Системы трех и двух твердых тел
При определении реакций связей системы тел основным является спо-
соб расчленения, при котором наряду с равновесием всей системы тел рас-
сматривается равновесие отдельных тел. При этом все остальные тела системы и соответствующие связи мысленно отбрасываются, а их действие на тело, равновесие которого рассматривается, заменяется реакциями.
Если возьмем равновесие всей механической системы, то реакции связей между телами, как силы внутренние, взаимно уравновешенные, не учитываются. При рассмотрении каждого тела в отдельности или какой-
нибудь группы тел, входящих в систему, реакции тех связей, которые были
мысленно удалены, становятся внешними силами и входят в уравнения равновесия.
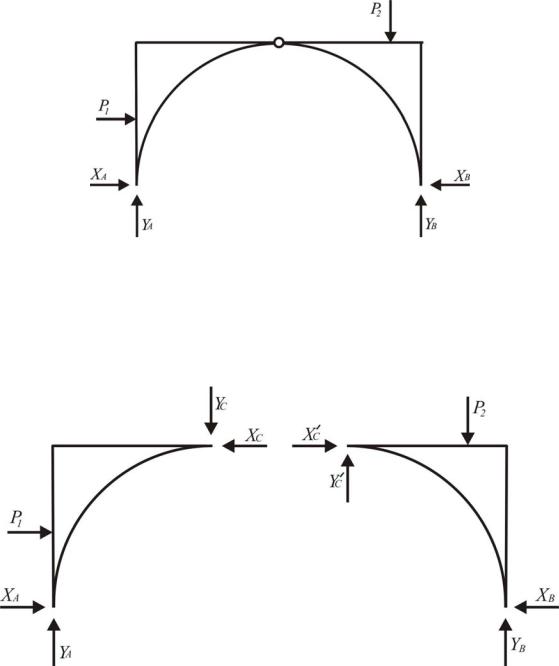
Пример . Определить реакции опор составной конструкции
(рис. 1.43), которая представляет собой трехшарнирную арку.
Рис. 1.43. Конструкция, состоящая из двух тел
31
Решение. Освобождаем арку от внешних связей.
Рис. 1.44. Вся конструкция с отброшенными внешними связями
Здесь 4 неизвестные силы и 3 уравнения равновесия.
Рассмотрим равновесие какой-либо одной полуарки. Отбрасываем мысленно шарниры А и С вместе с другой полуаркой.
Рис. 1.45. Конструкция, разделенная на два твердых тела
Для каждого твердого тела, находящегося под действием произвольной плоской системы сил можно составить 3 уравнения равновесия. Для двух
полуарок – 6 уравнений. Здесь 6 неизвестных реакций, т.е. задача опреде-
ления реакций статически определима.
Составим уравнения равновесия. При этом используем, например, всю конструкцию и левую часть арки.
32
Для всей системы:
1)Fkx 0, X A P1 X B 0;
2)Fky 0, YA YB P2 0;
3)M B 0, P2 d P1 a YA (b c d) 0.
Для левой части:
4)MС 0, P2 a X A 2a YAb 0;
5)Fkx 0, X A P1 XC 0;
6)Y 0, YA YC 0.
Решение удобно начать с третьего уравнения, так как оно содержит одно неизвестное YA:
YA (P2 d P1 a) / (b c d).
Далее из второго уравнения получаем:
YB YA P2 ;
из четвертого:
X A (YA b P2 a) / (2a) ;
из пятого:
XC X A P1 ;
из шестого:
YC YA ;
и, наконец, из первого:
X B X A P1.
1.8. Алгоритмизация расчета ферм методом вырезания узлов
1.8.1. Традиционный ручной расчет
Расчет ферм методом вырезания узлов сводится к последовательному рассмотрению условий равновесия сил, сходящихся в каждом из узлов фермы.
Рассмотрим в качестве примера ферму, изображенную на рис. 1.46.
33
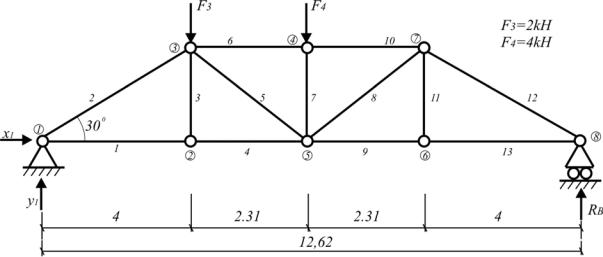
Рис. 1.46. Расчетная схема фермы
Число узлов п = 8. Число стержней т = 13.
Проверим соотношение m 2n 3. Получаем: 1 3 = 2 8 – 3. Значит, 13=13 – соотношение выполняется; следовательно, ферма из треугольников неизменяема и статически определима.
Решение, как правило, начинается с определения опорных реакций. Составляем уравнения равновесия для фермы в целом:
1. FKX 0; |
X A 0; |
2. FKY 0; |
Y1 F3 F4 RB 0; |
3. M1 0; |
F3 4 F4 6,31 RB 12,62 0. |
Из 3-го уравнения: |
8 4 6,31 2,63 кH. |
R |
|
B |
12,62 |
|
Из 2-го уравнения:
Y1 2 4 2,63 3,37 кH.
Проверка:
M8 0,
F2 6,31 F1 8,62 Y1 12,62 4 6,31 2 8,62 3,37 12,6242,48 42,52 0,04.
Ошибка вычислений составляет:
0,04 100 0,09 % .
42,48
34
Для определения 13 неизвестных внутренних усилий необходимо составить 13 уравнений равновесия. Для плоской системы сходящихся сил уравнения равновесия записываются в виде суммы проекций сил на любые две непараллельные оси:
Fkx 0;
Fky 0.
Будем последовательно отделять от фермы один узел за другим, рассматривая условия их равновесия. Начинаем с узла 1, где сходятся два стержня, так как из двух уравнений равновесия можно определить только два неизвестных усилия.
Узел 1 :
1. |
F |
0; |
S1 S2 cos30 |
|
|
|
|
||||
|
kx |
|
|
0, |
|
||||||
2. |
F |
0; |
|
|
|
|
|
|
|
|
|
|
ky |
|
Y S |
2 |
sin 30 |
|
0. |
|
|||
|
|
|
|
|
|
||||||
|
|
1 |
|
|
|
|
|
|
|
||
|
S2 6,74 кH (cжат); |
|
|
|
|||||||
|
S1 5,837 кH (растянут). |
|
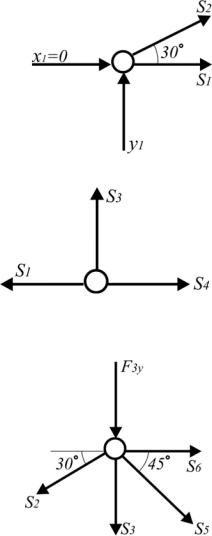
Рис. 1.47. Узел 1 |
||||||||
Узел 2 : |
|
|
|
|
|
|
|
|
|
|
|
3. Fkx 0; S1 S4 0; |
|
|
|
|
|
||||||
4. Fky 0; |
S3 0. |
|
|
|
|
|
|
|
|||
|
|
S4 5,837 кH. |
|
|
|
|
Рис. 1.48. Узел 2 |
||||
Узел 3 :
5.Fkx 0; S6 S cos 45 S2 cos30 0;
6.Fky 0; S2 sin 30 S3 F3 y S5 sin 45 0.
S4 5,837 кH.
Из 6-го уравнения: |
|
|
|
S5 |
3,37 2 |
1,638 кH. |
Рис. 1.49. Узел 3 |
|
0,707 |
|
|
Из 5-го уравнения:
S6 6,74 0,866 1,938 0,707 7,207 кH.
Узел 4 и т.д.
35

Четырнадцатое, пятнадцатое и шестнадцатое уравнения, составляемые для узлов 7 и 8, служат для проверки результатов.
Окончательные результаты сводятся в табл. 1.2.
Таблица 1 . 2
№ стержня |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
Усилия, кН |
5,84 |
-6,74 |
0 |
5,84 |
1,938 |
-7,207 |
4,0 |
-3,72 |
4,555 |
-7,2 |
0 |
-5,26 |
4,555 |
Усилия в стержнях 7–13 целесообразно проверить самостоятельно. Недостаток МВУ – погрешность при вычислении какой-нибудь силы
отражается на значениях последующих определяемых сил.
Для определения усилий в стержнях можно не находить предварительно реакции опор, а составить и решить систему из 16 уравнений (по два для 8 узлов ), в которых неизвестными будут 13 усилий в стержнях и 3 опорные реакции.
1.8.2. Алгоритмизация расчета для ЭВМ
Составленные уравнения равновесия могут быть записаны в матричной форме:
|
|
|
|
|
|
A |
|
|
|
, |
|
|
|
|
|
|
|
|
S |
P |
|
|
|||
|
1 |
cos30 |
0 |
0 |
0 |
0 |
. . . . |
0 |
|
|||
|
|
sin30 |
0 |
0 |
0 |
0 |
. . . . |
0 |
|
|||
|
0 |
|
||||||||||
|
|
0 |
0 |
1 |
0 |
0 |
. . . . 0 |
|
||||
|
1 |
|
||||||||||
где |
A 0 |
0 |
1 |
0 |
0 |
0 |
. . . . |
0 |
|
|||
|
0 |
cos30 |
0 |
0 |
cos 45 |
1 |
0 . . . |
0 |
|
|||
|
|
sin30 |
1 |
0 |
sin 45 |
0 |
0 . . . |
0 |
|
|||
|
0 |
|
||||||||||
|
|
. |
. . |
. |
. . . . . . |
|
||||||
|
. |
|
||||||||||
есть квадратная матрица размерностью 13 13, (m m) , составленная из коэффициентов перед внутренними усилиями;
S – вектор внутренних усилий размерностью т,
|
|
|
|
|
|
[S S |
|
S |
|
S |
|
.....S ]T ; |
||
S |
2 |
3 |
4 |
|||||||||||
|
|
|
|
|
|
|
1 |
|
|
13 |
||||
|
|
– вектор внешних сил размерностью т. |
|
|||||||||||
P |
|
|||||||||||||
|
|
|
|
[x |
y |
0 |
0 |
F |
F |
.....]T . |
||||
|
|
P |
||||||||||||
1 |
1 |
|
|
|
3x |
3 y |
|
|||||||
36
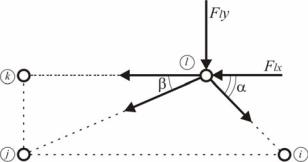
Для того чтобы ЭВМ могла сформировать уравнения равновесия узлов фермы, следует ввести в нее необходимые данные. Рассмотрим некоторый узел l.
Уравнение равновесия для этого узла имеет вид:
Рис. 1.50. Узел фермы
Fkx 0;
Sl k cos180 Sl j cos(180 ) Sl i cos Flx 0.
Fky 0;
Sl j sin(180 ) Sl i sin Fly 0.
Т.е. длясоставленияуравненийпроекцийдолжныбытьизвестны:
1)проекции действующих на узел l внешних сил;
2)узлы, с которыми узел l соединен стержнями;
3)узлы наклона стержней к осям.
Кроме того, должно быть известно общее количество стержней и узлов. Эту информацию можно дать следующим образом: пронумеруем все узлы фермы в последовательности, соответствующей порядку расчета методом вырезания узлов. Составим матрицу связей С, в которой показывается, какие узлы связаны между собой. Например, для фермы, представленной на рис. 1.51: n 6, m 9 .
1 |
2 |
|
|
|
|
3 |
|
1 |
|
||
|
2 |
|
|
|
3 |
||
|
2 |
4 |
|
3 |
4 |
|
|
C |
|
5 |
. |
3 |
|
||
|
4 |
5 |
|
|
4 |
6 |
|
|
|
||
5 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Размерностьэтойматрицы2 m. Сформируемвектор-столбецнагрузок
D F1x F1y x2 y2 0 0... T .
Компоненты этого вектора – проекции внешних сил на оси. Размерность его равна т.
37
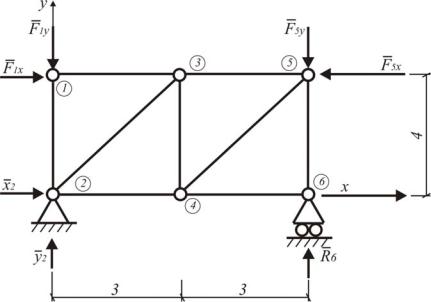
Рис. 1.51. Расчетная ферма
Нанесем на ферму декартову систему координат. Сформируем матрицу координат узлов размерностью (п узлов) (2 координаты):
xk |
yk |
|
|
|
|
|
|
0 |
4 |
1 |
|
|
0 |
|
|
0 |
|
2 |
|
|
4 |
|
3 |
B 3 |
|
||
3 |
0 |
|
4 |
6 |
4 |
|
5 |
|
0 |
|
6 |
6 |
|
||
|
|
|
|
|
|
|
|
С помощью этой матрицы и матрицы С определяются углы наклона стержней к осям.
Таким образом, исходная информация для ЭВМ содержит числа m, n и три указанные матрицы.
38
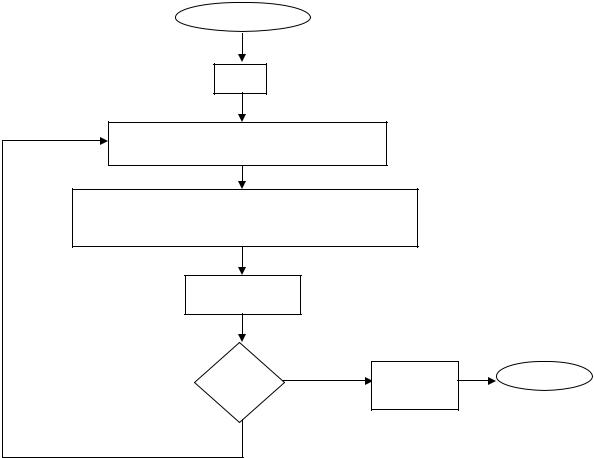
Алгоритм расчета может быть построен по следующей схеме:
начало
l 1
Определение углов наклона стержней l- го узла
Составление уравнений равновесия l-го узла. Определение неизвестных усилий.
l= l+1
l<n-1 |
Печатать |
Конец |
|
результат |
|
Рис. 1.52. Блок-схема расчета фермы методом вырезания узлов
1.9.Cтатически определимые
истатически неопределимые задачи
Статически определимыми называются задачи, которые можно решать методами статики твердого тела, т.е. задачи, в которых число неизвестных не превышает числа уравнений равновесия сил.
Статически неопределимыми называют задачи с числом неизвестных, превышающим число уравнений равновесия сил, т.е. задачи, которые нельзя решать методом статики твердого тела. Для решения нужно учитывать деформацию тела под нагрузкой.
Для плоской произвольной системы сил можно для тела составить три уравнения равновесия. Следовательно, в этом случае задача статически разрешима при числе неизвестных сил не более трех.
Для системы сходящихся сил можно составить два уравнения равновесия. Значит, решение возможно при числе неизвестных не более двух.
Если рассматривается система п тел, загруженная силами, произвольно расположенными на плоскости, то общее число уравнений статики 3п.
39
Значит, количество |
неизвестных сил в задачах статики для п тел |
m 3n. |
|
а |
б |
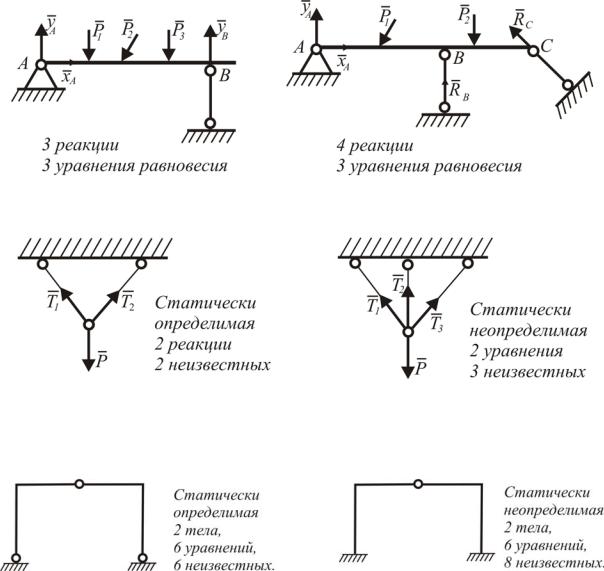
Рис. 1.53. Статическиопределимая(а) истатическинеопределимая(б) балки
а |
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.54. Статически определимая (а) и статически неопределимая (б) подвески
а |
|
б |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.55. Статически определимая (а) и статически неопределимая (б) рамы
1.10. Устойчивость при опрокидывании
Для тела, нежестко закрепленного наложенными на него связями, возникает важный вопрос об устойчивости равновесия.
Рычагом называется твердое тело, имеющее неподвижную ось вращения и находящееся под действием сил, лежащих в плоскости, перпендикулярной этой оси. Такой рычаг изображен на рис. 1.56. Через опорную точку О проходит ось вращения. На рычаг действуют силы P1, ..., Pn.
40
