
2351
.pdf
1.2.2. Условия равновесия плоской системы сходящихся сил
Очевидно, что для равновесия необходимо, чтобы равнодействующая равнялась нулю. В векторном виде
R 0 , |
(1.2.5) |
||
или |
|
|
|
Fk 0 , |
(1.2.6) |
||
т.е. силовой многоугольник должен быть замкнут.
Условия равновесия в аналитическом виде, или в виде проекций, на координатные оси можно записать на основе уравнения (1.2.3). Подкоренное выражение, содержащее сумму квадратов двух величин, может быть равно нулю, если одновременно равны нулю оба слагаемых под корнем, т.е.
Rx Fkx 0, |
|
|
|
(1.2.7) |
|
|
|
|
Ry Fkx 0. |
|
|
Итак, уравнения (1.2.7) выражают условия равновесия плоской системы сходящихся сил в аналитическом виде.
1.3. Теорема о трех непараллельных силах
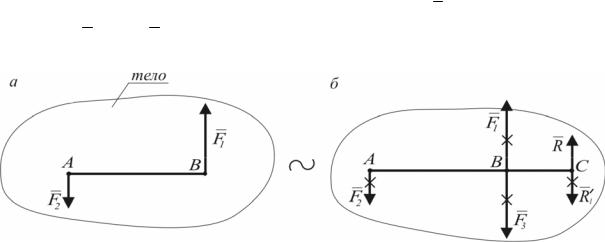
Теорема: если тело находится в равновесии под действием трех непараллельных сил, то линии действия этих сил пересекаются в одной точке.
Доказательство .
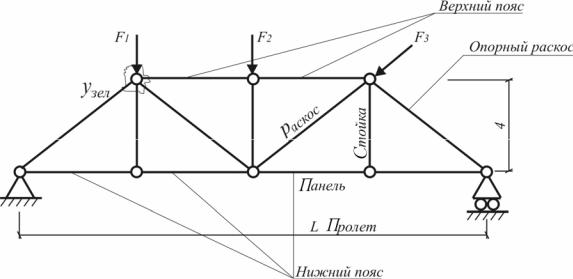
Пусть тело находится в равновесии под действием трех сил – F1 , F2 и F3 (рис.
1.10,а). Перенесем силы F2 и F3 в точку
пересечения их линий действия – точку О. Сложим две силы F2 и F3 (рис. 1.10,б).
Получаем, что тело находится в рав- новесии под действием двух сил – F и F1
(рис. 1.10, в). Следовательно, по первой аксиоме, эти силы направлены вдоль одной прямой. То есть сила F1 также прохо-
дит через точку О.
а
б
в
Рис. 1.10. Преобразование системы трех сходящихся сил
11
1.4. Расчет шарнирных ферм методом вырезания узлов
1.4.1. Понятие о ферме и терминология
Шарнирные фермы – это неизменяемые (жесткие) конструкции, образованные прямыми стержнями, соединенными по концам шарнирами. Если все стержни лежат в одной плоскости, ферма называется плоской. Места соединения стержней фермы называют узлами.
Рис. 1.11. Расчетная схема шарнирной фермы
Все внешние нагрузки к ферме прикладываются только в узлах. Будем считать стержни фермы невесомыми, а шарниры идеальными, т.е. без трения. Тогда можно считать, что на каждый из стержней фермы действуют две силы, приложенные к его концам, которые при равновесии могут быть направлены только вдоль стержня. Таким образом, стержни таких идеальных ферм работают только на растяжение или сжатие.
Все стержни, образующие ферму, разделяются на поясные и решетку. Поясными называются стержни, расположенные по внешнему контуру фермы. Они подразделяются на верхний пояс, очерчивающий верхнюю часть контура фермы, и нижний пояс, очерчивающий нижнюю часть контура фермы. Узловые шарниры на схемах ферм часто не показывают.
Решеткой называются внутренние стержни, служащие для соединения верхнего и нижнего поясов фермы. В решетке различаются вертикальные стержни или стойки и раскосы.
По характеру очертания контура фермы подразделяются на:
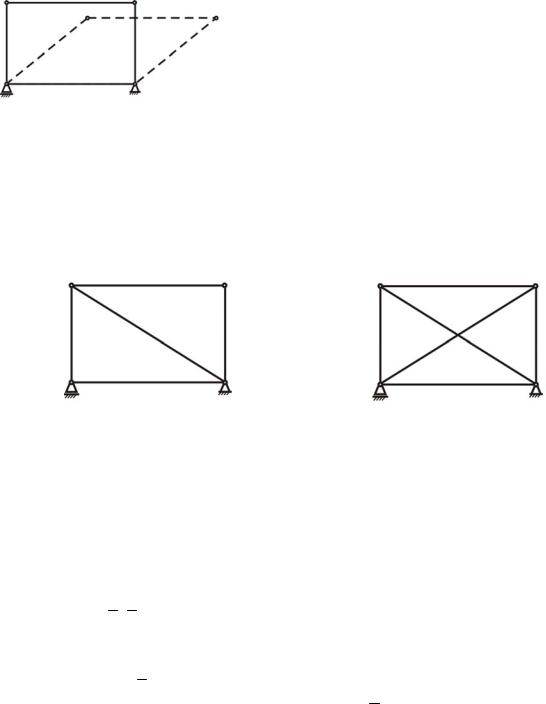
1) фермы с параллельными поясами, в которых оба пояса образованы двумя параллельными прямыми (рис.1.12):
12
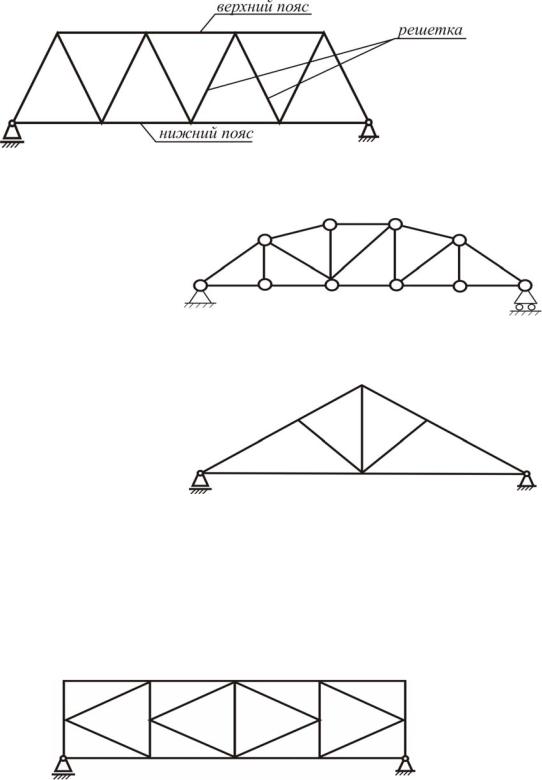
Рис. 1.12. Ферма с параллельными поясами
2) фермы с ломаным поя-
сом(рис. 1.13):
Рис. 1.13. Ферма с ломаным поясом
3) стропильные фермы
(рис. 1.14):
По виду решетки фермы подразделяются на:
1) решетчатые, в кото- Рис. 1.14. Стропильная ферма
рых решетка состоит из стоек или вертикалей и раскосов между ними (рис. 1.11).
2)раскосные, в которых решетка состоит только из наклонных стержней (см. рис. 1.12);
3)с полураскосной решеткой (рис. 1.15) (в панели вместо одного длинного раскоса делается два полураскоса):
Рис. 1.15. Полураскосная ферма
Все рассмотренные фермы известны под названием простых ферм, они получаются путем последовательного построения многоугольника из треугольников.
13
Зависимость k = 2n – 3 между числом шарниров п и числом стержней k устанавливает число возможных уравнений равновесия, необходимых для определения связевых усилий между шарнирами.
Если число стержней k < 2n – 3, то это соотношение показывает, что число стержней, служащих связью между шарнирами, меньше, чем это нужно для обеспечения неподвижности п шарниров; следовательно, ферма изменяема.
Примером изменяемой системы служит четы-
|
рехугольник, |
в |
котором k=4, 4 < 2 4–3=5 |
|
(рис. 1.16); приведение ее к неизменяемому |
||
|
виду может быть сделано путем дополнения |
||
|
пятого стержня – диагонали. Такая неизменя- |
||
Рис. 1.16. Изменяемая |
емая статически определимая система (k=5) |
||
приведена на рис. 1.17. Введение второй диа- |
|||
система |
гонали (рис. |
1.18) |
будет служить только для |
|
|||
лишнего закрепления и без того неизменяемой системы. Однако теперь число стержней k < 2n – 3, а число уравнений, необходимых для определения равновесия усилий в ферме, не изменится, и их будет недостаточно для определения усилий во всех стержнях.
Рис. 1.17. Неизменяемая статически |
Рис. 1.18. Неизменяемая статически |
определимая система |
неопределимая система |
1.4.2. Применение теоремы о трех силах к определению реакций опор ферм
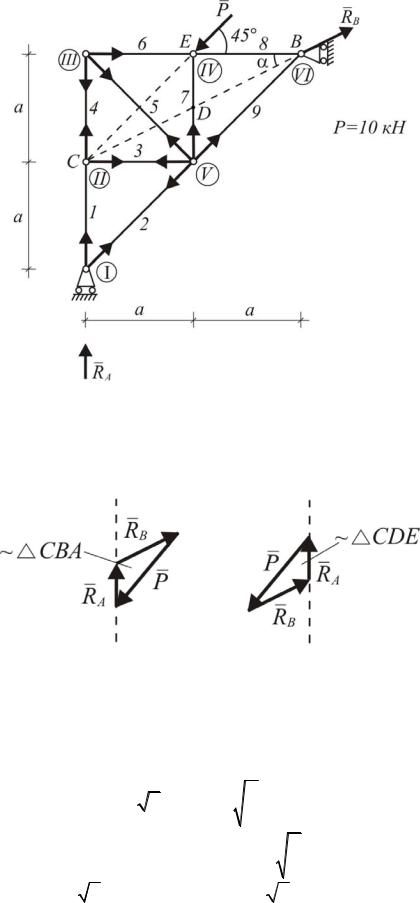
Если на ферму действует одна внешняя сила, опорные реакции можно определить с помощью теоремы о равновесии трех непараллельных сил
(рис. 1.19) – P, RA и RB .
Определим реакции в опорах. Так как опора А – подвижная, то линия действия RA известна, она направлена перпендикулярно основанию опоры
А. Направление RB определим по теореме о трех силах – она направлена из т. В в точку пересечения сил линий действия RA и Р – точку С.
14
А
Рис. 1.19. Расчетная схема фермы
Строим замкнутый силовой треугольник (рис. 1.20). Его построение начнем с силы Р.
а |
б |
Рис. 1.20. Силовой треугольник
Из подобия силового многоугольника треугольнику CDE находим опорные реакции RA и RB:
|
|
|
|
|
|
P |
|
RA |
|
|
|
RB |
; |
|
|
|
|
|
|
|
|
|
CE |
DE |
CD |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
EC a 2, |
CD a |
5 , |
|
ED a |
; |
|||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
|
2 |
|
||
R |
A |
|
P a2 |
3,535 кH, R |
|
P a |
54 |
7,906 кH. |
||||||||
|
|
|
||||||||||||||
|
|
a |
2 |
|
|
|
B |
|
|
a |
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
15
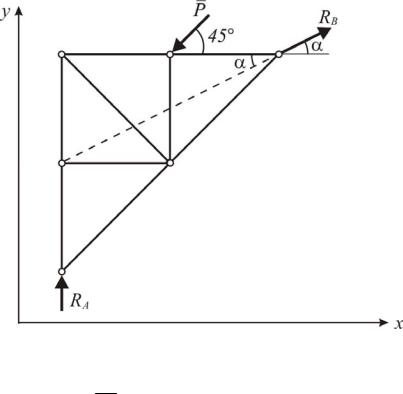
Аналитическое определение реакций. Условия равновесия всей фермы под действием трех сходящихся сил приведены на рис. 1.21.
Рис. 1.21. Равновесие фермы как твердого тела
tg 2aa 0,5; arctg 0,5 26,565 ; sin 0,447; cos 0,894.
|
|
|
RB cos 0, |
|
FKX 0, |
P cos 45 |
|||
|
F 0, |
P sin 45 |
R |
sin 0. |
|
||||
|
KY |
|
B |
|
RB P cos 45 7,07 7,905 кH. 0,894 0,894
RA 10 0,707 7,905 0,447 3,536 кH.
Далее определяем усилия в стержнях фермы.
1.4.3. Определение усилий в стержнях методом вырезания узлов
Этим методом удобно пользоваться, если надо найти усилия во всех стержнях фермы. Пронумеруем узлы римскими цифрами, а стержни – арабскими. Искомые усилия обозначим S1, S2 и т.д. соответственно номеру
стержня. Отрежем мысленно все узлы со сходящимися в них стержнями от остальной фермы. Действие отброшенных частей стержней заменим силами, которые будут направлены вдоль соответствующих стержней и численно равны искомым усилиям S1, S2 …
16
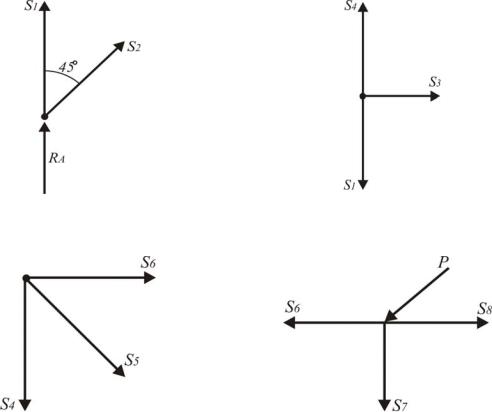
Изображая силы «вырезанного» узла на рисунке, направляем их от узлов, т.е. считая все стержни растянутыми. Если в результате расчета величина усилия в каком-нибудь стержне получается отрицательной, это означает, что данный стержень не растянут, а сжат.
Для сил, сходящихся в каждом узле, составляем уравнение равновесия
Fкх 0, |
Fкy 0 . |
Первым вырезается тот узел, в котором сходится не более двух стержней.
Начинаем с узла I:
Fkx 0, S2 sin 45 0, S2 0.
Fky 0, RA S1 0, S1 RA 3,535 кH.
Зная S1, переходим к узлу II:
Fkx 0, S3 0.
Fky 0, S1 S4 0.
S4 S1 3,535 кH.
Рис.1.22. Узел I |
Рис. 1.23. Узел II |
Дальнейший расчет (узел III, узел IV и т.д.) производим аналогично.
Рис.1.24. Узел III |
Рис.1.25. Узел IV |
Порядок вырезания узлов должен быть таким, чтобы в рассматриваемом узле было не более 2 неизвестных усилий.
17
Если в узле, не загруженном внешними силами, сходятся три стержня, из которых два направлены вдоль одной прямой, то усилие в третьем стержне равно нулю (например, S3=0 узел II).
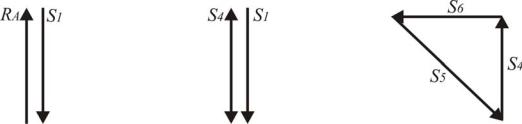
Расчет методом вырезания узлов может производиться графически в той же последовательности. Для этого, отсекая от фермы каждый из ее узлов, находят усилия в стержнях и строят соответствующие замкнутые силовые многоугольники. Построения производятся в определенном масшта-
бе (рис. 1.26, 1.27, 1.28).
Рис. 1.26. Векторный |
Рис. 1.27. Векторный |
||||||||||||||||||||
многоугольник |
многоугольник для уз- |
||||||||||||||||||||
для узла I |
|
|
|
|
|
|
|
A |
|
|
ла II |
|
|
|
|
|
|
|
|
|
|
|
S1 |
|
R |
|
|
S4 |
|
S1 |
|||||||||||||
Рис. 1.28. Векторный многоугольник для узла III
Xi 0; |
|
|
n |
|
|
|||
X0 Xi |
0; |
|||||||
|
|
|
|
|
n |
i 1 |
|
|
Yi |
|
|
|
|
|
|
||
0; |
Y0 Yi 0; |
|
||||||
|
|
|
|
|
i 1 |
|
|
|
|
M |
|
0; |
n |
M |
|
0. |
|
|
0 |
|
io |
|
||||
|
|
|
|
|
||||
|
|
|
|
i 1 |
|
|
|
|
Значение усилий определяется измерением соответствующего отрезка в силовом многоугольнике. Знак усилия находится сравнением направления вектора на силовом многоугольнике и на исходном вырезанном узле. Если направление совпадает – знак «+», не совпадает – знак «–».
Окончательныерезультатырасчетасводятсявтаблицу(табл. 1.1).
|
|
|
|
|
Таблица 1 . 1 |
||
|
Таблица усилий в стержнях фермы |
|
|
|
|||
|
|
|
|
|
|
|
|
№ стержня |
1 |
2 |
3 |
4 |
|
… |
п |
Усилия, кН |
-3,535 |
0 |
0 |
-3,535 |
|
|
|
18
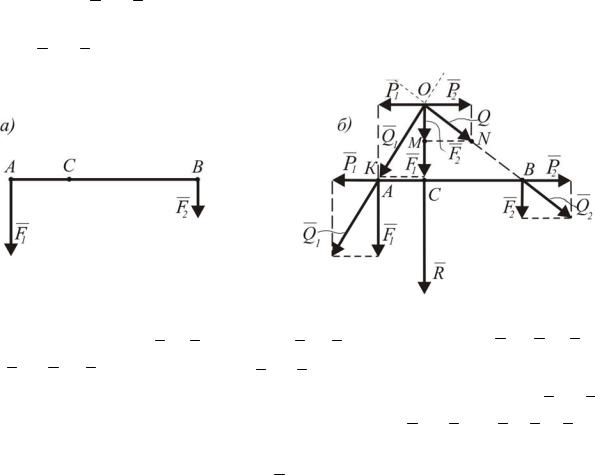
1.5.Система параллельных сил
1.5.1.Параллельные силы, направленные в одну сторону
Пусть F1 и F2 параллельные силы, приложенные в точках А и В, при-
чем F1>F2 (рис. 1.29). Приложим в точках А и В уравновешенную систему сил P1 и P2 ( P1 P2 ).
Рис. 1.29. Сложение параллельных сил, направленных в одну сторону
Сложим силы P1 и F1 , а также P2 и F2 . Получим силы Q1 F1 P1 и Q2 F2 P2 . Перенесем силы Q1 и Q2 в точку пересечения их линий действия О и разложим их на прежние составляющие. Отбросим силы P1 и P2 как взаимно уравновешенные и сложим силы F1 и F2 . R F1 F2 , и
R F1 F2 ,
Перенесем полученную силу R по линии ее действия в точку С, лежащую на пересечении линии действия этой силы с отрезком АВ. Таким образом, система параллельных сил заменяется одной силой – равнодействующей. Величина равнодействующей равна сумме модулей слагаемых сил.
Определим местоположение точки приложения равнодействующей – точки С.
AOC ~ KOL ,
COB ~ MON .
Из подобия треугольников следует:
AC |
OC |
, |
(1.5.1) |
|
P |
||||
F |
|
|
||
1 |
1 |
|
|
|
BC |
OC |
, |
(1.5.2) |
|
P |
||||
F |
|
|
||
2 |
2 |
|
|
19
или
P1 OC F1 AC, |
(1.5.3) |
||
|
|
|
|
P2 OC F2 BC. |
|
||
Выражая из обоих уравнений ОС и приравнивая полученные правые |
|||
части, запишем |
|
|
|
F1 AC F2 BC, |
(1.5.4) |
||
или |
|
|
|
|
F1 |
BC . |
(1.5.5) |
|
F |
||
|
AC |
|
|
2 |
|
|
|
Т.е. точка приложения равнодействующей делит отрезок между силами
всоотношении, обратно пропорциональном к этим силам.
1.5.2.Параллельные силы, направленные в противоположные стороны
Примем для определенности F1 F2 . Пусть сила F1 приложена в точке В, а сила M0 r F – в точке А (рис. 1.30).
Рис. 1.30. Сложение параллельных сил, направленных в разные стороны
Приложим в некоторой точке С, лежащей на продолжении прямой АВ со стороны большей силы, уравновешенную систему сил R и R . Пусть
уравновешенные силы по величине составляют:
|
|
|
R F2 F1 , |
(1.5.6) |
||||||
аположениеточкиСприложения |
|
|
и |
|
подчиняетсясоотношению |
|||||
R |
R |
|||||||||
|
|
|
|
|
R |
|
AB . |
(1.5.7) |
||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
BC |
|
|
|
|
|
|
F |
|
|
|
|
|
2 |
|
|
|
|
||||||
Силы |
|
и F2 можно заменить их |
равнодействующей F3: |
|||||||
R |
||||||||||
F3=R’+ F2= F1– F2+ F3= F1; причем сила F3, согласно соотношению (1.5.7),
20
