
2351
.pdf
Разделяя переменные v и x, получим: vdv k2 xdx .
Проинтегрируем это уравнение:
12 v2 12 k2 x2 c1.
Постоянную интегрирования определим из начальных условий: при t = 0
x = a ,
значит,
c1 12 k2a2 ,
v k a2 x2 .
Учитывая, что v dx / dt , произведем вторичное интегрирование уравнения:
dx |
k a2 |
x2 ; |
||
dt |
dx |
|
|
|
|
|
kdt. |
||
|
|
a2 x2 |
||
|
|
|
||
kt arccos ax c2.
При t = 0
x = a ,
значит,
c2 arccos1 0.
kt arccos |
x |
; |
x |
cos kt; |
|
a |
a |
||||
|
|
|
x a cos kt.
131
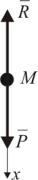
3.4.2. Сила, зависящая от скорости (Падение тела при учете силы сопротивления движению)
Примем силу сопротивления пропорциональной скорости движения:
R v.
Исходное дифференциальное уравнение движения имеет вид
mx Fkx.
Для нашей задачи это уравнение примет вид:
mx mg x . |
|
Рис. 3.10. Падение |
|
|
тела при учете силы |
||
Сокращая на массу и вводя обозначение k / m , |
сопротивления |
||
движению |
|||
получим: |
|
|
|
|
x g kx , |
|
|
или |
|
|
|
|
dv g kv. |
|
|
|
dt |
|
|
Разделяя переменные, получим: |
|
|
|
|
dv |
dt . |
(*) |
|
g kv |
||
|
|
|
|
Введем обозначение:
U g kv.
Тогда
dU kdv, dv dUk .
Теперь уравнение (*) можно переписать в виде:
|
dU kdt. |
||
|
|
U |
|
Интегрируя, получаем: |
|||
|
lnU kt C1, |
||
|
ln(g kv) kt C1. |
||
При t 0 v0 0, |
C1 ln g. |
||
|
ln |
g kv |
kt. |
|
|
||
|
|
g |
|
132
Потенцируя последнее выражение и делая элементарные преобразования, получаем:
gkv е kt , g
g kv gе kt ,
v g gе kt . k k
x gk t kg2 е kt С2.
Определим постоянную интегрирования С2: при t = 0 x 0, С2 kg2 .
Уравнение движения получает вид
x gk t kg2 (l kt 1).
Интерес представляет частный случай: при t v g / k, т.е. с течением времени скорость точки становится постоянной.
3.5. Колебания материальной точки
Колебательное движение материальной точки происходит при условии, если на точку, отклонен-
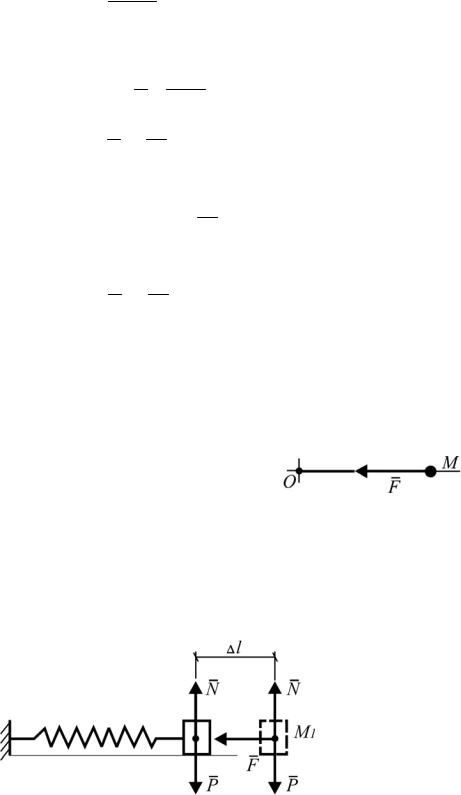
ную от положения покоя, действует сила, стремя- Рис. 3.10. Восстанавли- щаяся вернуть точку в это положение. Такая сила вающая сила
называется восстанавливающей (рис. 3.10).
Рассмотрим практически важный случай, когда восстанавливающая сила пропорциональна отклонению точки от положения покоя: F c OM ,
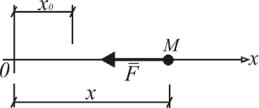
где с – коэффициент пропорциональности. Например, сила упругости пру-
жины (рис. 3.11).
Рис. 3.11. Сила упругости пружины Fупр с l
133
Определим физический смысл коэффициента с для упругой пружины. Этот коэффициент называется жесткостью пружины. Восстанавливающая сила, или сила упругости, F c l, где l – удлинение или укоро-
чение пружины. При l=1, F=c. Следовательно, жесткость пружины численно равна силе, необходимой для растяжения или сжатия пружины на единицу длины.
В зависимости от характера и совокупности переменных сил, действующих на материальную точку, различают четыре основных вида колебательного движения точки:
1)свободные колебания – под действием только восстанавливающей
силы;
2)затухающие колебания – под действием восстанавливающей силы и силы сопротивления движению;
3)вынужденные колебания – под действием восстанавливающей силы
исилы периодического характера, называемой возмущающей силой;
4)вынужденные колебания при наличии сопротивления движению. Здесь действуют восстанавливающая сила, сила сопротивления движению, возмущающая сила.
3.5.1. Свободные колебания
Поместим начало координат в положение покоя точки О, а ось х направим вдоль прямолинейного отклонения ОМ точки М, тогда восстанавливающая сила (рис. 3.12)
F c OM с x . |
(3.5.1) |
Рис. 3.12. Восстанавливающая сила |
|
Дифференциальное уравнение движения будет иметь вид |
|
mx F. |
(3.5.2) |
Подставив восстанавливающую силу, выраженную через координату, получим:
mx cx, |
(3.5.3) |
|||
или |
|
|
||
x |
c |
x 0. |
(3.5.4) |
|
m |
||||
|
|
|
||
134
Введем обозначение |
|
|
||
k2 |
c |
, |
(3.5.5) |
|
m |
||||
|
|
|
||
тогда уравнение движения примет вид |
|
|
||
x k2 x 0. |
(3.5.6) |
|||
Это уравнение называется дифференциальным уравнением свободных колебаний.
Его решение ищем в виде:
x ezt . |
|
(3.5.7) |
||||
Подставив это выражение в уравнение движения, получим: |
|
|||||
z2ezt k2ezt 0, |
|
|||||
ezt (z2 k2 ) 0. |
(3.5.8) |
|||||
Выражение в скобках называется характеристическим уравнением. Его |
||||||
решение |
z1 ik, |
|
|
|||
|
|
|
||||
|
z2 ik |
|
|
|||
или |
|
|
|
|
|
|
z1,2 ik, |
|
|
||||
где 0 . |
|
|
|
|
|
|
Таким образом, имеем два независимых решения: |
|
|||||
x |
|
e( ik )t , |
|
|
||
1,2 |
|
|
|
|
|
|
или |
|
|
t |
|
|
|
x1 |
e |
sin kt, |
|
|||
|
|
(3.5.9) |
||||
x |
|
|
|
|
|
|
e t cos kt. |
|
|||||
2 |
|
|
|
|
|
|
Общее решение дифференциального уравнения можно представить в |
||||||
виде линейной комбинации двух независимых решений |
|
|||||
x Ax1 Bx2 , |
|
(3.5.10) |
||||
или |
|
|
|
|
|
|
x Asin kt Bcos kt . |
(3.5.11) |
|||||
Взяв производную по времени, получим выражение для скорости дви- |
||||||
жения: |
|
|
|
|
|
|
x Ak cos kt Bk sin kt . |
(3.5.12) |
|||||
При t 0
x x0 , x v0 .
135
Подставив эти начальные условия в уравнения (3.5.11) и (3.5.12), получим:
x0 B, |
|
, |
(3.5.13) |
||
|
|
|
|
||
v0 Ak, |
|
|
|||
A |
v0 |
. |
|
|
(3.5.13) |
|
|
|
|||
|
k |
|
|
|
|
Подставив в уравнение (3.5.11) вместо А и В их значения, выраженные
через начальные условия, получим окончательно: |
|
||
x |
v0 |
sin kt x cos kt. |
(3.5.14) |
|
|||
|
k |
0 |
|
|
|
|
|
Уравнению (3.5.11) можно придать другой, амплитудный вид, сделав
замену постоянных А и В другими постоянными и : |
|
А a cos , |
(3.5.15) |
B asin . |
(3.5.16) |
Тогда |
|
x a cos sin kt asin cos kt, |
(3.5.17) |
или |
|
x asin(kt ) . |
(3.5.18) |
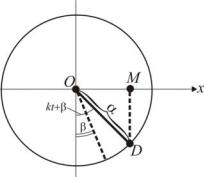
Рис. 3.13. Круговая аналогия
Если колебания совершаются по закону синуса (или косинуса), то такое движение называется гармоническими колебаниями; следова-
тельно, свободные колебания – гармонические колебания.
Здесь можно увидеть аналогию с вращательным движением отрезка ОD вокруг точки O.
Значение координаты x точки D x OM asin(kt ) .
Здесь – начальный угол движения, или начальная фаза колебаний;
а– максимальная координата x точки D, или амплитуда колебаний;
kt+ – фаза колебаний;
k – угловая скорость вращения, или круговая частота колебаний.
136
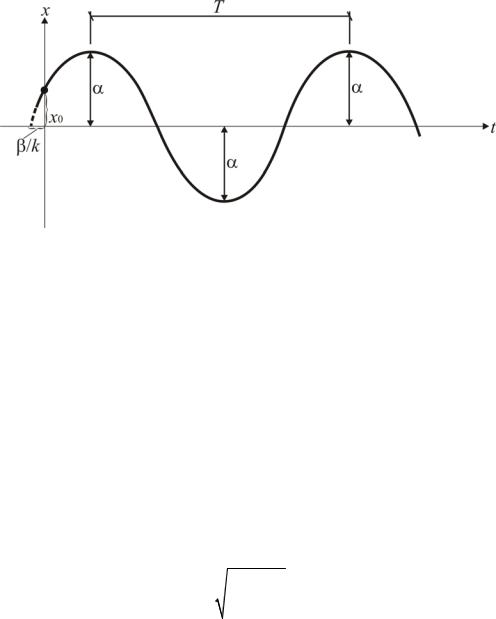
Период колебаний (время, за которое точка приходит в одно и то же положение с одной и той же стороны), или время одного оборота отрезка ОD, определим из соотношений
kt1 kt2 2 , k(t1 t2 ) 2 ,
kT 2 ,
T |
2 |
. |
(3.5.19) |
|
|||
|
k |
|
|
Рис. 3.14. График свободных колебаний
Постоянные а и определим из начальных условий: при t=0 x x0 , x v0 .
Выражение для скорости точки получим из уравнения (3.5.18), дифференцируя его по времени:
x аk cos(kt ) . |
(3.5.20) |
Подстановка начальных условий в уравнение (3.5.18) и выражение для скорости (3.5.20) дает:
x0 v0
Таким образом, постоянные а
a
sin x0 / a,
asin , |
(3.5.21) |
||||
|
|
|
|
||
ak cos . |
|
||||
и можно представить в виде |
|
||||
x |
2 |
|
v2 |
|
|
|
|
0 |
, |
(3.5.22) |
|
|
|
||||
0 |
|
k2 |
|
||
|
|
|
|
||
cos v0 / (ak). |
(3.5.23) |
||||
137
При свободных колебаниях частота и период определяются из соотношений
|
c |
|
|
||
k |
, |
|
|||
m |
|||||
|
(3.5.24) |
||||
|
|
||||
T |
|
2 |
. |
||
|
|
||||
|
c / m |
||||
|
|||||
Эти соотношения показывают, что период и частота свободных колебаний от начальных условий не зависят.
Пример . Груз массой m=10 кг, подвешенный на пружине жесткостью с=1960 Н/м, отвели на 2 см вниз и отпустили. Найти уравнение колебательного движения груза.
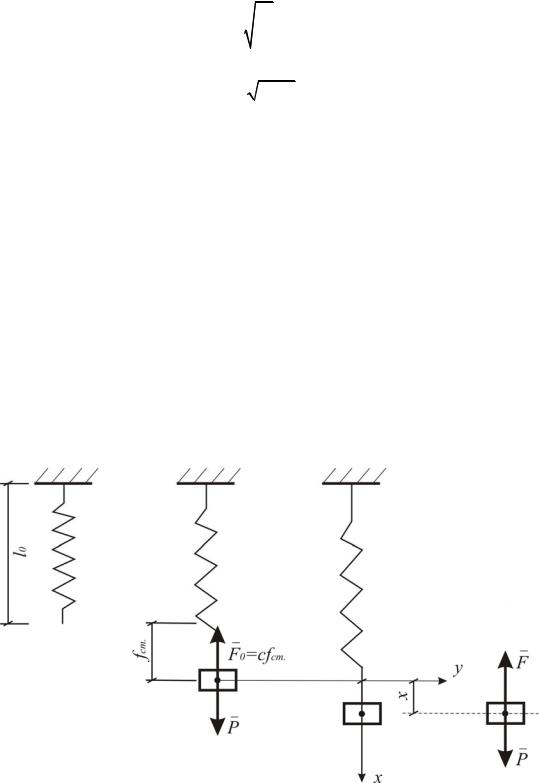
Решение. На рис. 3.15 изображены: а) недеформированная пружина; б) груз в положении статического равновесия; в) промежуточное положение колеблющегося на пружине груза; г) силы, действующие на колеблющуюся массу в промежуточном положении.
По рис. 3.15,г составим уравнение движения:
|
mx P F, |
где |
F c( fст x). |
|
Следовательно, |
|
mx P cfст cx. |
а |
б |
в |
г
Рис. 3.15. Иллюстрация положений груза
138
В положении статического равновесия P Fуп сfст ; следовательно, mx cx 0,
x mc x 0.
Введем обозначение:
k2 mc .
Тогда
x k 2 x 0.
Это дифференциальное уравнение свободных колебаний. Его решение: x asin(kt ) .
a |
x |
2 |
|
v2 |
|
2 |
|
|
|
|
|
0 |
|
0,02 |
|
0 |
0,02 м. |
||
|
|
|
|||||||
|
0 |
|
k2 |
|
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
tg , |
. |
|
|||
|
|
|
|
|
|
|
|
2 |
|
|
k |
1960 / 10 14 |
c 1. |
||||||
Таким образом, уравнение движения принимает вид
x0,02sin 14t .
2
Период свободных колебаний T 2 6,28 0,45 c. 14 14
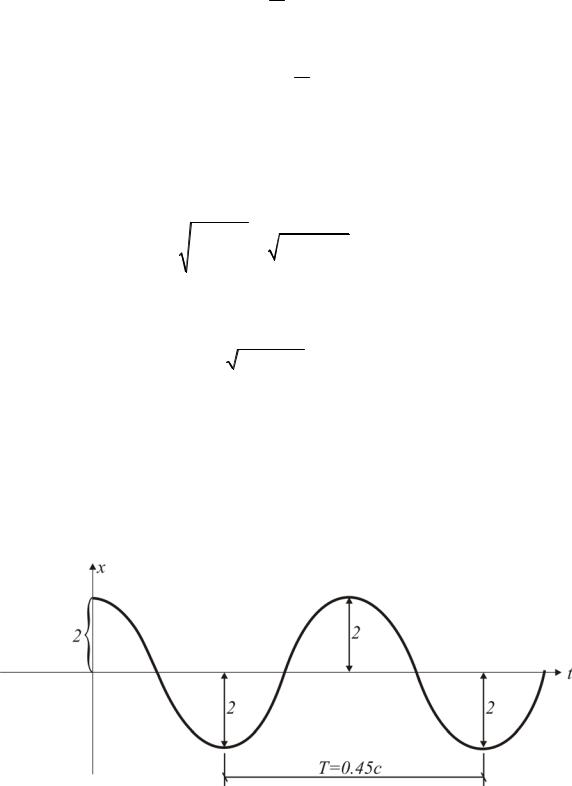
График колебательного движения представлен на рис. 3.16.
Рис. 3.16. График свободных колебаний груза для данного примера
139
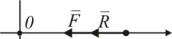
3.5.2. Затухающие колебания материальной точки
Рассмотрим влияние сил сопротивления на колебательное движение точки, а также выясним характер этого движения в зависимости от величины силы сопротивления.
В реальных условиях колебательный процесс всегда проходит при сопротивлении движению (трение, сопротивление воздуха и т.д.). Это означает, что кроме восстанавливающей силы, направленной к центру колебаний, на точку действует сила сопротивления, направленная в сторону, противоположную движению. Закон изменения величины силы сопротивления зависит от природы этой силы. Например, модуль силы трения скольжения можно принять постоянным, а величину силы сопротивления воздуха или жидкости при невысоких скоростях – пропорциональной скорости движения.
|
|
|
|
|
Рассмотрим последний случай, ко- |
|||
x |
|
гда сила сопротивления |
движению |
|||||
Рис. 3.17. На движущую точку дей- |
|
пропорциональна скорости: |
|
|||||
ствуют восстанавливающая сила и |
|
|
|
|
|
|
R v. |
(3.5.25) |
сила сопротивления движению |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Дифференциальное уравнение движения mx Fkx примет вид |
||||||||
|
mx F R , |
(3.5.26) |
||||||
или |
|
|
|
|
|
|
|
|
mx cx x, |
(3.5.27) |
|||||||
x |
|
x |
|
c |
x 0. |
(3.5.28) |
||
|
|
|
||||||
|
m |
|
m |
|
||||
Введем обозначения: |
|
|
|
|
|
|
|
|
|
|
|
|
2n, |
(3.5.29) |
|||
|
|
m |
||||||
|
|
|
|
|
|
|||
|
|
c |
|
k2. |
(3.5.30) |
|||
|
|
m |
||||||
|
|
|
|
|
|
|||
Таким образом, дифференциальное уравнение движения приобретет |
||||||||
вид |
|
|
|
|
|
|
|
|
x 2nx k2 x 0. |
(3.5.31) |
|||||||
Решение этого дифференциального уравнения будем искать в виде:
x ezt . |
(3.5.32) |
140
