2314

их, затрачивая на ионизацию определенную энергию. Вследствие локального выделения тепла, в которое переходит теряемая электронами энергия, в жидкости образуются паровые пузырьки. Если давление в жидкости больше давления насыщенных паров при данной температуре, то паровые пузырьки, порождаемые ионизирующими частицами высоких энергий, будут быстро исчезать. Кавитация на паровых зародышах развивается, либо когда давление в жидкости длительное время меньше давления насыщенных паров, либо за счет пульсации давления.

В жидкости, вследствие броуновского движения, имеют место флуктуации внутренней структуры – области пространства с молекулами низкой энергии и молекулами высокой энергии. В областях с молекулами высокой энергии, которые называют областями повышенной микро-темпе- ратуры, звуковые волны могут обеспечить значения напряжений, достаточных для разрыва сплошности жидкости [128].

Стабильное существование парогазовых пузырьков объясняется тем, что на поверхности пузырька имеются равномерно распределенные одноименные заряды, обусловленные находящимися в жидкости ионами. Отталкивание этих зарядов предотвращает смыкание пузырька [198, 227].

Условие равновесия парогазового пузырька в жидкости записывается в виде

При распространении в жидкости гармонических колебаний без учета Рэ и диффузии газа через поверхность пузырька, но с учетом изотермичности процесса роста пузырька с радиусом R, уравнение равновесия записывается как [6]:

где Р0 – начальное давление в пузырьке, Па; Ра – акустическое давление, Па; R0 – начальный радиус пузырька, м; Р – статическое давление в жидкости, Па.

Пузырек устойчив, пока Ра не достигает критического значения Ркр. При Ра > Ркр пузырек начинает быстро расти, что приводит к разрыву сплошности жидкости.

Значение критического радиуса определяется по формуле:

С учетом того, что давление насыщенных паров значительно меньше гидростатического давления, уравнение для кавитационной прочности

32

жидкости в зависимости от начального радиуса пузырька записывается в виде

R03 R02 2 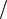P 32 3 27P P Pкр 2 0. (2.5)

Для заданного переменного давления и частоты звукового поля существует минимальный и максимальный радиус пузырьков, способных вызвать кавитацию. Максимальный соответствует резонансному радиусу, который определяется по формуле Миннерта [6]:

где = cp / сv – соотношение удельных теплоемкостей для газа и пара в пузырьке.

Формула (21.6) может быть использована для гармонических колебаний пузырька при небольших амплитудах, для низких частот звукового поля и крупных пузырьков. Для высоких частот более применима формула, выведенная Хабеевым при учете фазовых переходов и поверхностного натяжения, которая описывает зависимость резонансного радиуса

где Ар – функция, зависящая от теплоты парообразования, плотности, теплопроводности и температуры жидкости. По мере увеличения частоты акустического поля, кавитацию вызывают только пузырьки с большей fp, т.е. пузырьки меньшего радиуса, чем Rp.

Порог кавитации и его частотная зависимость определяются объемом жидкости. Величина кавитационной прочности жидкости зависит от наибольшего зародыша из всех имеющихся в объеме жидкости. Вероятность попадания в озвучиваемую зону зародыша большего размера возрастает с увеличением объема озвучиваемой жидкости [9].

Нелинейное дифференциальное уравнение, описывающее простую модель сферически-симметричной пульсации газовой полости радиусом r = R(t) в поле плоской звуковой волны, имеет вид:

Аналитическое решение этого уравнения, получено Рэлеем при простейших условиях: P Pa ; P(R) = 0. В этом случае уравнение (2.8) перехо-

дит в уравнение захлопывания пустой полости под действием гидростатического давления:

33

ВремязахлопыванияпустойполостиопределяетсяизформулыРэлея[6]:

Уравнение, описывающее изменения радиуса кавитационной полости в поле ультразвуковой волны известно, как уравнение Нолтинга-Неппайреса:

Уравнение (2.11) достаточно хорошо описывает поведение кавитационного пузырька в поле ультразвуковой волны, но допущения о несжимаемости жидкости не позволяют правильно оценить конечную стадию захлопывания кавитационного пузырька.

Динамику кавитационного пузырька с учетом сжимаемости описывает уравнение Херринга-Флинна (2.12). Уравнение (2.12) более точно описывает динамику кавитационного пузырька с учетом сжимаемости, но неаде-

кватно при скоростях движения, сравнимых со скоростью звука c0 , что характерно для конечной стадии захлопывания пузырька.

Этот недостаток устранен в уравнении Кирвуда-Бете, выведенного с допущением о сферичности волн конечной амплитуды, образующихся при захлопывании полости:

34

A = 300 МПа, B = 300 МПа, n = 7.

Уравнения (2.11), (2.12) и (2.13) не решаются в общем виде. Их численные решения получают для конкретных частных случаев с определенными значениями частоты и амплитуды звукового поля и величиной начального размера пузырька. Исследование этих уравнений сделано подробно в [9, 227, 294] и показывает, что при амплитудах звукового давления Ра < Pкр газовые пузырьки не захлопываются и пульсируют линейно. Пузырьки с R < Rр пульсируют с частотой акустической волны, а при размере пузырька R > Rр период пульсации близок к периоду собственных колебаний. При Ра > Pкр движение полости становится неустойчивым и она захлопывается в первом положительном полупериоде. При дальнейшем увеличении Ра инерционные силы препятствуют захлопыванию пузырька, и он совершает одно или несколько колебаний, а затем схлопывается. Все эти результаты достаточно хорошо согласовываются с экспериментом [9, 198, 294].

При расширении кавитационного пузырька в жидкость излучается сферическая волна. Без учета вязкости и теплопроводности давление в волне определяется по формуле Джилмора:

При очень большой скорости захлопывания пузырька излучаемая волна может перейти в ударную, давление в которой изменяется обратно пропорционально расстоянию от полости r [6]. Расстояние, на котором образуется ударная волна, определяется значением максимального давления в полости и соответствует соотношению:

где Рmax составляет сотни мегапаскалей.

Динамика парогазовой полости с учетом теплообмена и частично – динамики газа в пузырьке рассматривалась в работах М.А. Маргулиса [128, 129]. Для описания движения стенки пузырька использовалось дифференциальное уравнение (2.8). Скорость газа Vг(R, t) в пузырьке определялась из уравнения неразрывности. Масса газа m(R, t) в пузырьке радиусом R считалась неизменной.

35

Давление в пузырьке равно

где 0 Ri R0.

Уравнение теплопроводности для газа внутри кавитационного пузырька имеет вид:

где гcп T (Ri ,t) 1 .

По результатам численных решений этих уравнений был сделан вывод, что теплообмен в процессе схлопывания пузырька оказывается весьма существенным, значительно понижающим максимальные параметры парогазовой смеси внутри кавитационного пузырька: скорость и температуру – более чем в 2 раза, а давление – более чем на порядок по сравнению с адиабатическим схлопыванием. Время схлопывания в адиабатическом режиме и с учетом теплообмена незначительно отличается от рэлеевского времени для пустого пузырька.

Минимальный радиус пузырька Rmin и радиус Rc, при котором достигается максимальная скорость при учете теплообмена, почти вдвое превышают соответствующие величины для адиабатического схлопывания. Максимальная скорость движения стенок пузырька при учете теплообмена (не более 600 м/с) значительно меньше скорости звука в жидкости (с0 1500 м/с), поэтому вклад слагаемых, содержащих dR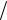dtc0 в уравне-

ниях Херринга-Флинна и Кирквуда-Бете, должен быть значительно меньше, чем для модели адиабатического схлопывания [129]. Эти выводы подтверждаются экспериментальными исследованиями [100, 146], согласно которым конечный радиус кавитационного пузырька всего в 3–5 раз меньше исходного.

В большинстве исследований кавитации, особенно теоретических, рассматривают поведение единичного пузырька. В реальных условиях необходим целый комплекс мер, чтобы добиться существования одиночного пузырька. Даже при давлении, ненамного превышающем порог кавитации, сразу появляется множество кавитационных пузырьков, занимающих определенную часть пространства, которую называют кавитационной областью [181]. При импульсных растягивающих напряжениях в жидкости зародыши кавитации начинают расти, образуя кавитационный кластер, форма и длина которого определяются начальным спектром размеров кавита-

36

ционных зародышей, характером прикладываемого напряжения и граничными условиями. Все зародыши достигают максимального размера одновременно, и среда может считаться практически монодисперсной, содержащей пузырьки только одного размера [151].

При малых расстояниях между пузырьками в плотном кавитационном кластере кавитационные пузырьки взаимодействуют друг с другом в процессе пульсаций. В этом случае в уравнение (2.11) необходимо ввести слагаемое, выражающее давление, генерируемое соседними пузырьками. Запишем уравнение (2.11), учитывая давление, генерируемое всеми кавитационными пузырьками Pкав:

Рассмотрим отдельную область кавитационных пузырьков, равномерно распределенных в пространстве с постоянной плотностью п [170]. Каждое схлопывание пузырька производит волну давления и делает свой вклад во вторичное давление Pкав в уравнении (2.19). Точное решение уравнения (2.19) требует решения отдельного уравнения для каждого кавитационного пузырька.

Произведем некоторые упрощения. Примем, что все пузырьки имеют одинаковый размер и внешние условия одинаковы для всех пузырьков. Следовательно, каждый из пузырьков кавитационного кластера схлопывается в момент времени tс и излучает волну давления Pкав1, одинаковую для всех пузырьков. Общее вторичное давление Pкав находится как суперпозиция всех волн давления, взятых в количестве, ограниченном временем распространения волны. Выделим в кавитационном кластере сферу радиусом r, включающую множество кавитационных пузырьков. В центре сферы находится рассматриваемый пузырек. В пределах ограниченного объе-

ма вклад всех пузырьков будет составлять пPп(t tс r c) Rmin dr , при d 4 r2dr . Интегрируя по всему объему, получаем:

Pкав(t) пRmin Pп(t tс r c) dr

или

где t tс cr .

37

При = 0, t > tс уравнение (2.19) принимает вид:

(воздух) эта величина равна B = 0,953; Г – гамма-функция. Для t < tc вторичное давление равно нулю.

В развитой кавитационной области количество кавитационных пузырьков превышает количество зародышей примерно в 105 раз. Это объясняется тем, что процесс возникновения кавитационных пузырьков является цепной реакцией [196]. Кавитация, возникшая на единичном зародыше, за время в несколько десятков периодов ультразвуковых колебаний развивается в стабильную область, состоящую из множества кавитационных пузырьков.

Процесс развития кавитационной области представляется следующим образом. При захлопывании кавитационный пузырек может терять устойчивость и распадаться на части, а так как давление и температура в этот момент в пузырьке максимальны, то давление и температура парогазовой смеси в образовавшихся «осколках» тоже повышены. В фазе растяжения они легко расширяются и становятся новыми зародышами кавитации, менее прочными, чем постоянно имеющиеся в жидкости. Кавитационные полости, возникшие на этих зародышах, порождают новые. Внутри кавитационной области идет непрерывный процесс размножения и коагуляции кавитационных пузырьков, причем кавитационный порог несколько уменьшается, так как в установившемся режиме роль кавитационных зародышей начинают выполнять равновесные пузырьки, объем и газосодержание у которых больше, чем у зародышей [181].

Акустическая кавитация в жидкостях инициирует различные физикохимические явления; сонолюминесценцию (свечение жидкостей); химические эффекты (звукохимические реакции); эрозию твердого тела (разрушение поверхности); диспергирование (измельчение твердых частиц в жидкости) и эмульгирование (смешивание и гомогенизация несмешивающихся жидкостей).

Сонолюминесценция и звуковые химические реакции являются генетически связанными процессами, могут оказывать взаимное влияние, но в принципе они могут осуществляться независимо один от другого [128, 129]. Ультразвуковая люминесценция и свечение, возникающее при гидродинамической кавитации, являются близкими по своей природе процессами.

38

При экспериментальном исследовании кавитации в низкочастотных звуковых полях была выявлена аналогия по физико-химическим эффектам между низкочастотной и ультразвуковой кавитацией [128, 129].

Модель физико-химических процессов, происходящих в кавитационном пузырьке и прилегающем к нему объеме жидкости, представляют в следующем виде [128]. В кавитационную полость могут проникать пары воды, растворенные газы, а также вещества с высокой упругостью пара и не могут проникать ионы или молекулы нелетучих растворенных веществ. Выделяющейся в процессе схлопывания пузырька энергии достаточно для возбуждения, ионизации и диссоциации молекул воды, газов и веществ с высокой упругостью пара внутри кавитационной полости. На этой стадии любой из присутствующих газов является активным компонентом, участвуя в передаче энергии возбуждения, перезарядке и других процессах. Действие звукового поля на вещества, проникающие в полость, является непосредственным, прямым, причем действие активных газов О2, Н2 и N2 в кавитационной полости двойственное: во-первых, О2 и Н2 участвуют в реакциях трансформирования радикалов:

Н О2 НО2 , ОН Н2 Н Н2О,

а N2 – в газовых звукохимических реакциях, конечным результатом которых является фиксация азота:

N2 O2 )))NO2 , N2 H2 )))NH3 ;

во-вторых, химически активные газы, проникая в кавитационную полость, участвуют, так же как и благородные газы, в передаче энергии электронного возбуждения молекулам воды, а также в процессе перезарядки. Здесь символом))) обозначено химическое действие звука.

При схлопывании кавитационного пузырька в раствор переходят радикалы Н+, ОН-, ионы и электроны малой энергии, образовавшиеся в газовой фазе при расщеплении молекулы Н2О и веществ с высокой упругостью пара, продукты их взаимодействия и частичных рекомбинаций, а также метастабильные возбужденные молекулы Н2О.

Суммарную схему кавитационного расщепления молекул воды представляют в следующем виде:

H2O )))H , OH , H2 , H2O2.

возникающие в системе активные частицы после перехода в раствор сольватируются и реагируют с растворенными веществами. На этой стадии, когда осуществляются косвенные действия акустических колебаний, на ход процесса могут оказывать влияние практически только химически активные газы – О2 и Н2.

39

Вконечном счете, воздействие кавитации на водные растворы сводится

кединственному процессу – расщеплению молекул воды в кавитационных пузырьках. Независимо от природы растворенных веществ, звук действует на одно вещество – на воду, что приводит к изменению ее физико-хими- ческих свойств: увеличению рН, электропроводности воды, увеличению числа свободных ионов и активных радикалов, структуризации и активации молекул.

2.2. Электрическая и дипольно-ориентационная гипотеза природы кавитационных явлений

Различные исследования процесса кавитации и выдвигаемые многочисленные гипотезы, объясняющие эти явления, позволяют сделать только один вывод: природа первичной активации молекул внутри кавитационного пузырька является либо электрической, либо дипольно-ориента-

ционная модель [128, 129, 202, 204].

Исторический обзор электрических гипотез кавитации проведен в работе М.А. Маргулиса [130]. Электрические гипотезы основаны на идее возникновения электрического разряда в газовой фазе. Кратко остановимся лишь на последних версиях таких гипотез – гипотезе Маргулиса [129, 130] и Липсона [122].

Основные положения теории Маргулиса сводятся к следующему. В жидкости у поверхности раздела с кавитационным пузырьком образуется двойной электрический слой. Согласно схеме Штерна – Гельмгольца, можно условно выделить близкую к поверхности плотную часть двойного слоя и более удаленную диффузную часть, где адсорбционными силами можно пренебречь и ионы могут перемещаться в жидкости. Независимо от способа создания кавитации при движении кавитационных пузырьков происходит многократное и быстрое обновление поверхности раздела фаз. Образование поверхностного потенциала может быть обусловлено либо ориентационным эффектом, либо присутствием ионов примесей. Примеси могут присутствовать в столь ничтожном количестве (~ 7·108 см-3), что их практически невозможно определить аналитически, они не влияют на физико-химические свойства жидкости, но участвуют в образовании поверхностного заряда. Образование двойного слоя на поверхности раздела фаз является общим свойством жидкостей (не обязательно воды).

Нескомпенсированный электрический заряд образуется в результате возникновения акустических потоков, которые смывают часть диффузного двойного слоя. Пульсация кавитационных пузырьков приводит к потере устойчивости их сферической формы, при этом возникают деформации и как предельный случай – расщепление пузырьков.

40