
2175
.pdf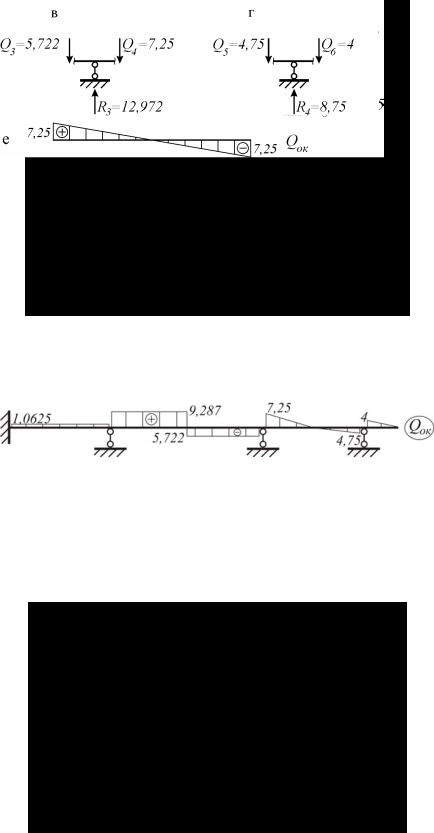
Эту формулу для участка, ограниченного параболой представим графически (рис. 8.2):
Рис.8.2
Определяем опорные реакции, которые равны «скачку» на эпюре Qок
(рис. 8.3).
Рис. 8.3
Проверка Qок . Найденные опорные реакции должны уравновесить внешнюю нагрузку (рис. 8.4):
Fky 0 F g 8 R1 R2 R3 R4
15 2 8 1,0625 8,2245 12,972 8,75 0.
Рис. 8.4
111

Расчет неразрезной балки от действия временной нагрузки
Рис. 8.5
От временной нагрузки расчет выполняем, используя фокусные отношения.
При загружении одного пролета в неразрезной балке эпюра моментов в незагруженных пролетах имеет нулевую точку, которая называется моментным фокусом. Положение этой точки постоянно и не зависит от интенсивности и вида нагрузки загруженного пролета, а зависит от соотношения жесткости и длины пролетов (рис. 8.5).
Различают левые и правые моментные фокусы. Левым (правым) моментным фокусом называется нулевая точка эпюры моментов данного пролета при загружении пролетов, расположенных правее (левее) рассматриваемого. Поскольку фокусные точки в каждом пролете имеют постоянное положение, то отношение моментов незагруженного пролета является постоянной величиной.
Левое фокусное отношение K лев |
|
Mn 1 |
bn 1 . |
|||
|
|
|||||
n 1 |
|
|
Mn 2 |
|
an 1 |
|
|
|
|
|
|||
Правое фокусное отношение K пр |
|
|
Mn |
|
аn 1 . |
|
|
|
|
||||
n 1 |
|
|
Mn 1 |
bn 1 |
||
|
|
|
|
|||
Для определения левых и правых фокусных отношений используются следующие формулы:
где l
n
ln
In I0
лев |
|
|
|
|
l |
|
|
|
1 |
|
|
|
|||
Kn 1 |
2 |
|
|
n |
|
|
2 |
|
|
|
|
; |
|||
|
|
|
лев |
||||||||||||
|
|
|
|
|
|
|
|
kn |
|
|
|
||||
|
|
|
|
ln 1 |
|
|
|
|
|||||||
пр |
|
|
|
|
l |
|
|
|
1 |
|
|
||||
Kn 1 |
2 |
|
|
n |
|
2 |
|
|
|
, |
|||||
|
|
пр |
|||||||||||||
|
|
|
|
|
|
|
|
|
kn |
|
|
||||
|
|
|
|
|
ln 1 |
|
|
|
|
||||||
– приведенная длина l l |
|
|
I0 |
; |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||
|
n |
|
n In |
|
|
|
|
|
|
|
|
||||
– геометрическая длина пролета,
– момент инерции сечения n-пролета;
– момент инерции сечения любого пролета (лучше взять наименьшее сечение).
112
|
|
|
EI0 EI; |
|
|
|
|||
|
l |
l EI0 6 EI |
6; |
||||||
|
1 |
1 EI |
|
EI |
|
|
|
||
|
|
|
1 |
|
|
|
|
|
|
l |
l |
EI0 9 |
EI |
|
|
3; |
|||
3EI |
|
|
|||||||
|
2 |
|
2 EI2 |
|
|
|
|
||
l |
l |
EI0 6 |
|
EI |
|
|
4. |
||
1,5EI |
|||||||||
3 |
|
3 EI3 |
|
||||||
Определяем левые фокусные отношения, рассматривая балку слева
направо. Для жесткой заделки фокусное отношение равно 2, |
kлев 2. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
лев |
|
|
|
l |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
6 |
|
|
|
|
|
1 |
|
|
k2 |
2 |
|
1 |
|
, |
|
2 |
|
|
|
|
2 |
|
|
|
2 |
|
2 3 5; |
||||||||
|
|
|
лев |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
k1 |
|
|
|
|
|
|
3 |
|
|
|
|
|
2 |
|
||
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
k лев 2 |
l |
|
|
|
|
|
1 |
|
|
2 |
3 |
|
|
|
1 |
|
2 1,35 3,35. |
|||||||||
|
2 , |
|
2 |
|
|
|
|
|
|
2 |
|
|
||||||||||||||
|
|
|
лев |
|
|
|
|
|
|
|||||||||||||||||
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
k2 |
|
|
|
|
|
4 |
|
|
|
5 |
|
|
||||||
|
|
l3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Правые фокусные отношения определяем, рассматривая балку справа
налево, для шарнирной опоры фокусное отношение равно , |
kпр . |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
пр |
|
l |
|
|
|
1 |
|
|
4 |
|
1 |
|
|
8 |
|
|
||||
k2 |
2 |
3 |
|
2 |
|
|
|
2 |
2 |
|
|
|
|
2 |
|
4,67; |
|
|||
|
пр |
|
|
|
|
|||||||||||||||
|
|
|
|
|
k3 |
|
|
3 |
|
|
|
|
3 |
|
|
|||||
|
|
l2 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
k |
пр 2 |
l2 |
|
2 |
|
|
2 |
3 |
2 |
|
|
|
2,893. |
|
||||||
|
пр |
|
|
|
|
|||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
k2 |
|
|
6 |
|
|
4,67 |
|
|
|
|||||
|
|
|
l1 |
|
|
|
|
|
|
|
|
|||||||||
Для загруженного равномерно-распределенной нагрузкой n-го пролета моментынаопорахопределяютсяпоследующимформулам:
Mn 1 |
ql2 knпр 1 |
Mn |
ql2 knпр 1 |
||||
4 |
|
; |
4 |
|
. |
||
knл knпр 1 |
knл knпр 1 |
||||||
Временная нагрузка – равномерно-распределенная, действует по всей длине балки. Предполагаем, что временная нагрузка действует в первом
пролете: |
|
2 62 |
|
2,893 1 |
|
||
M0 |
|
7,12 кН м; |
|||||
4 |
2 2,893 |
1 |
|||||
|
|
|
|||||
M1 |
|
2 62 |
|
2 1 |
|
3,76 кН м. |
|
4 |
2 2,893 1 |
||||||
|
|
|
|||||
113
На других опорах находим моменты, используя фокусные отношения:
|
|
|
|
|
M2 |
M1 |
|
3,76 |
0,805 кН м; |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k2пр |
|
|
|
|
|
|
4,67 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
M3 |
|
M2 |
|
0,805 0. |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
k3пр |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Временная нагрузка во втором пролете см. расчет в таблице. |
||||||||||||||||||||||||||||||||||||||||||
Временная нагрузка в третьем пролете: |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
2 6 |
2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
18(1 0) |
|
18 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
M2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5,37 кН м; |
||||||||||||||||||||
4 |
3,35 |
1 |
|
|
3,35 |
|
|
1 |
|
|
3,35 |
0 |
3,35 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
М3 |
2 62 |
|
|
|
|
3,35 1 |
0; |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
3,35 |
1 |
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
М1 |
|
|
|
М2 |
|
|
5,37 |
1,075 кН м; |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
k2лев |
|
|
|
|
5 |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
М |
0 |
|
|
|
|
М1 |
|
|
1,075 0,537 кН м. |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
k лев |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Временная нагрузка на консоли: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М3 4 кН м; |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
М |
2 |
|
|
М3 |
|
|
|
4 |
1,194 кН м; |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k лев |
|
|
3,35 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
М1 |
|
|
|
М2 |
|
1,194 0,239 кН м; |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
k2лев |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
М |
0 |
|
М1 |
|
|
0,239 0,12 кН м. |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
лев |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Построение объемлющих (огибающих) эпюр M и Q.
Постоянная нагрузка действует всегда, а временная нагрузка может действовать, а может и не действовать. Необходимо найти такое сочетание постоянной и временных нагрузок, которые вызывают в сечениях наибольшие и наименьшие изгибающие моменты и поперечные силы.
Для определения максимального момента Мmax в данном сечении к моменту от постоянной нагрузки Mпост прибавляют все положительные
моменты от временной нагрузки Mвр в данном сечении. Для определения минимального момента Мmin в данном сечении к моменту от постоянной
114
нагрузки Mпост прибавляют все отрицательные моменты от временной нагрузки Mвр в данном сечении
Mmax Mпост Мвр; Мmin Mпост Мвр.
Аналогично этому строят Qmax и Qmin
Qmax Qпост Qвр;
Qmin Qпост Qвр.
Расчет Mmax |
и Mmin можно выполнить в табличной форме. |
|
|||||||
|
|
|
|
|
|
|
|
|
|
Номер |
Mпост |
|
|
М |
вр |
|
Мmax |
Мmin |
|
|
|
|
|
|
|
||||
сечения |
|
в 1-м |
во 2-м |
|
в 3-м |
На |
|||
|
|
пролете |
пролете |
|
пролете |
консоли |
|
|
|
|
|
|
|
|
|
||||
0 |
0,250 |
|
-7,12 |
3,375 |
|
-0,537 |
0,12 |
3,825 |
-7,694 |
a |
6,625/ |
|
3,560 |
-1,638 |
|
0,269 |
-0,060 |
10,454/ |
4,928/ |
|
-11,375 |
|
|
|
|
|
|
-7,546 |
-13,073 |
1 |
-5,000 |
|
-3,76 |
-6,650 |
|
1,075 |
-0,239 |
-3,925 |
-15,649 |
b |
22,830 |
|
-2,238 |
11,150 |
|
-1.075 |
0.239 |
34,219 |
19,517 |
c |
11,250 |
|
-1,478 |
13,300 |
|
2,148 |
0,478 |
27,176 |
7,624 |
2 |
-11,500 |
|
0,805 |
-7,250 |
|
-5,370 |
1,194 |
-9,501 |
-24,120 |
d |
1,250 |
|
0,403 |
-3,625 |
|
6,315 |
-1,403 |
7,968 |
-3,778 |
3 |
-4,000 |
|
0 |
0 |
|
0 |
-1,000 |
-4,000 |
-8,000 |
Эпюры моментов от последовательного загружения пролетов временной нагрузкой показаны на рис. 8.6, б,д. Окончательные (огибающие или объемлющие) эпюры моментов показаны на рис. 8.6,е.
115

Рис. 8.6
116

Варианты задания 8
117

118

119
Исходные данные к заданию 8
|
|
Длины, м |
|
|
Соотношение |
|
Постоянная нагрузка |
||||||||
№ |
|
|
жесткостей пролетов |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
п/п |
a |
l1 |
l2 |
l3 |
l4 |
n1EI |
n2EI |
n3EI |
n4EI |
F1 |
F2 |
q1 |
q2 |
M |
|
|
|
|
|
|
|
n1= |
n2= |
n3= |
n4= |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
10 |
11 |
12 |
13 |
14 |
15 |
1 |
2 |
6 |
9 |
12 |
6 |
1,5 |
3 |
3 |
|
1 |
8 |
12 |
4 |
2 |
18 |
2 |
2 |
9 |
9 |
6 |
6 |
1,5 |
1,5 |
2 |
|
1 |
24 |
12 |
3 |
4 |
20 |
3 |
1 |
12 |
9 |
6 |
9 |
2 |
3 |
2 |
|
3 |
6 |
18 |
1,5 |
3 |
36 |
4 |
1 |
9 |
12 |
6 |
9 |
3 |
3 |
1 |
|
1 |
12 |
18 |
4 |
1 |
12 |
5 |
3 |
6 |
12 |
9 |
12 |
1 |
2 |
3 |
|
3 |
24 |
6 |
1,5 |
3 |
6 |
6 |
3 |
12 |
6 |
12 |
6 |
2 |
1 |
3 |
|
1,5 |
28 |
12 |
2 |
2 |
20 |
7 |
2 |
6 |
9 |
6 |
12 |
1 |
1,5 |
1 |
|
2 |
30 |
10 |
4 |
3 |
22 |
8 |
2 |
12 |
9 |
6 |
6 |
3 |
1,5 |
1 |
|
1,5 |
6 |
12 |
4 |
1 |
27 |
9 |
1 |
9 |
9 |
6 |
12 |
1 |
1,5 |
2 |
|
3 |
36 |
12 |
2 |
3 |
14 |
10 |
1 |
12 |
6 |
9 |
6 |
3 |
1 |
1,5 |
|
1 |
10 |
30 |
1,5 |
4 |
24 |
11 |
3 |
9 |
6 |
12 |
9 |
1,5 |
1 |
2 |
|
1 |
30 |
12 |
4 |
2 |
16 |
12 |
3 |
6 |
12 |
12 |
6 |
2 |
2 |
3 |
|
1 |
12 |
16 |
3 |
1 |
28 |
13 |
2 |
12 |
12 |
6 |
6 |
3 |
2 |
1,5 |
|
1 |
8 |
18 |
4 |
1,5 |
16 |
14 |
2 |
9 |
12 |
9 |
6 |
1 |
2 |
1,5 |
|
1,5 |
8 |
10 |
1,5 |
2 |
12 |
15 |
1 |
9 |
6 |
6 |
12 |
1,5 |
1 |
1 |
|
2 |
12 |
24 |
2 |
3 |
14 |
16 |
1 |
6 |
12 |
12 |
3 |
1 |
3 |
2 |
|
1 |
6 |
8 |
3 |
1,5 |
10 |
17 |
3 |
9 |
6 |
6 |
12 |
1,5 |
1 |
1,5 |
|
3 |
10 |
18 |
4 |
3 |
18 |
18 |
3 |
9 |
9 |
12 |
6 |
1 |
1,5 |
2 |
|
1,5 |
30 |
12 |
2 |
4 |
22 |
19 |
2 |
12 |
6 |
6 |
12 |
3 |
1,5 |
1 |
|
2 |
6 |
10 |
1,5 |
3 |
20 |
20 |
2 |
12 |
9 |
6 |
6 |
3 |
3 |
1,5 |
|
1 |
8 |
12 |
4 |
2 |
12 |
21 |
1 |
6 |
9 |
6 |
12 |
1 |
3 |
1,5 |
|
2 |
10 |
18 |
1,5 |
3 |
16 |
22 |
1 |
9 |
12 |
6 |
6 |
1 |
2 |
1,5 |
|
1 |
16 |
24 |
2 |
1 |
12 |
23 |
3 |
12 |
6 |
6 |
12 |
3 |
1 |
1,5 |
|
2 |
18 |
12 |
2 |
4 |
20 |
24 |
3 |
12 |
9 |
9 |
6 |
2 |
1 |
1,5 |
|
1 |
24 |
10 |
4 |
1,5 |
30 |
120
