
2074
.pdfПри выборе распределения Chi I (Хи-квадрат) строка df – число степеней свободы (целое положительное число), вероятность соответствия р=0,95. Нажав Compute в строке Chi I, увидим: 0,95 – квантиль хи- квадрат-распределение с df степенями свободы. Его используют при исследовании оценки дисперсии нормальной выборки, а также при проверке зависимостей в таблицах сопряженности и в критериях согласия.
При рассмотрении оценки среднего и неизвестной дисперсии выборки используют выборочную дисперсию и t-распределение. Данное распределение применяется в регрессионном анализе и анализе временных рядов. В списке распределений оно – t (Student) (t-распределение Стьюдента). Число степеней свободы – df. При степенях свободы более 30 t-распределение практически совпадает со стандартным нормальным распределением.
F-распределение возникает в регрессионном, дисперсионном и дискриминантном анализе, а также при многомерных анализах данных. Степень свободы 1 – df1, степень свободы 2 – df2.
Аналогично работают и с другими распределениями. Более подробно данные вопросы рассмотрены в специальной литературе.
3.1.3. Построение гистограмм
Вдоль правого края панели имеются кнопки с графиками. Верхняя кнопка обозначена красным графиком и гистограммой. После нажатия на нее появляется панель (Возле строки 5). На ней кнопка с красными графиками. Нажимаем на нее (под клавишей ОК).
Появляется панель Grafics Gallery (рис. 3.10). Выделяем строки, как показано на рис. 3.10. Нажимаем ОК. Появившаяся панель (рис. 3.11) позволяет выбрать необходимый закон распределения. При нажатии кнопки Variables выбираем тип графика Graf type (у нас факторы S и Т). Так как два фактора, то выбираем Multiple. Вид распределения выбираем в Fit Tup. В левом нижнем углу кнопки дополнительных возможностей: Cumulative counts; Breaks between counts; Shov percentages. Количество интервалов задается цифрой у правого края (у нас 13). ОК. Появляется график гистограмм (рис.3.12). По совпадению с законом распределения выбранного закона визуально судится о правомочности выбора.
161
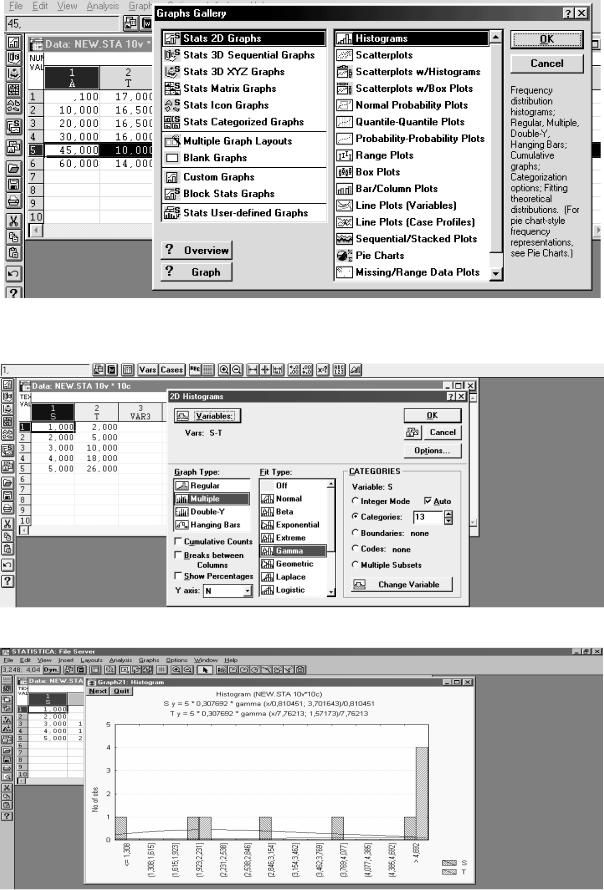
Рис.3.10. Панель выбора графика
Рис.3.11. Панель выбора закона распределения
Рис.3.12. Панель с графиком закона распределения выборки
162
3.2. Обработка данных модулем «Нелинейное оценивание»
Nonlinear Estimation
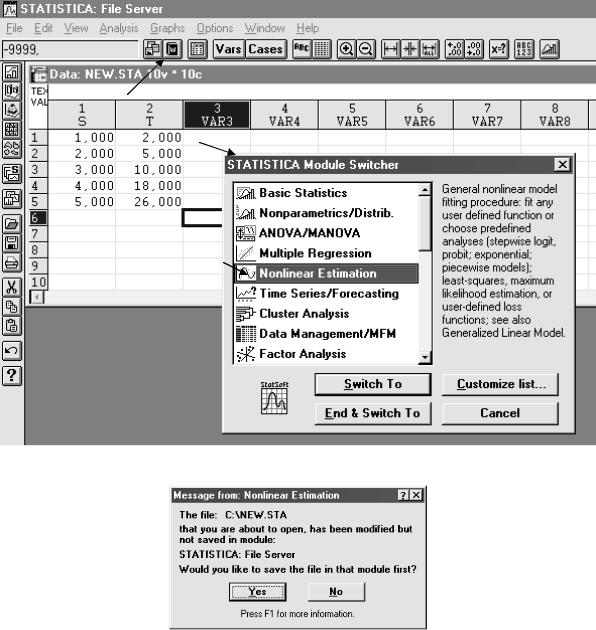
После подготовки базы данных запускается соответствующий модуль расчета: вторая строка, вторая кнопка слева (три зеленых листочка с графиками), называемая (желтым текстом) STATISTICA Module Swicher.
После нажатия на кнопку появится экран (рис. 3.13). Выбирается нелинейное оценивание (как на рис. 3.13) – нажимаем Enter. Появится запрос на использование данных из файлов сервера (рис. 3.14). Нажать Yes.
Рис. 3.13. Выбор модуля обработки данных STATISTICA Module Swicher
Рис. 3.14. Выбор источника данных
Выбираем вид функции уравнения регрессии: User-specified regression – Определенная пользователем регрессия; Logistic regression –
163
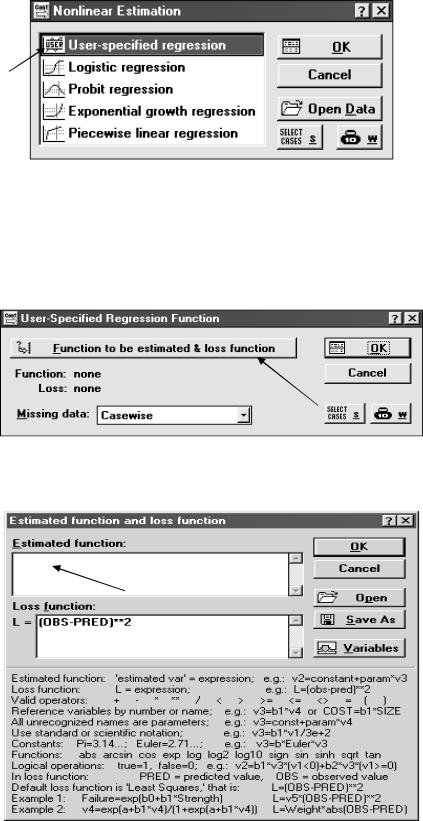
Логистическая регрессия; Exponential growth regression – Регрессия экспоненциального роста; Piecewise linear regression – Кусочно-линейная регрессия. Принимаем функцию, задаваемую пользователем (рис. 3.15).
Рис.3.15. Стартовая панель модуля Нелинейное оценивание
Появляется окно (рис.3.16). Кнопка Select Cases – Выбрать случаи – задаются условия выбора случаев. Кнопка 10-W позволяет приписать разные веса переменным. Мы ее не используем. Нажимаем клавишу с зеленой стрелкой Function to be…
Рис.3.16. Запуск окна для выбора уравнения регрессии
Появляется окно для набора уравнения функции (рис.3.17).
Рис.3.17. Запуск окна для набора уравнения регрессии
164
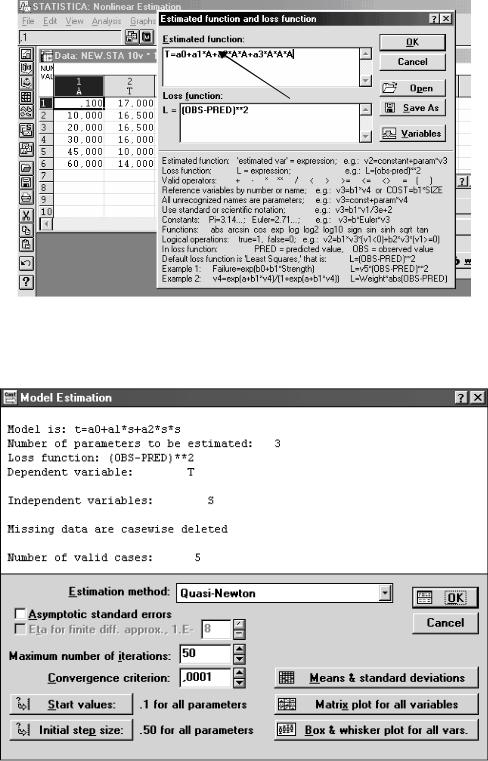
Вводим уравнение предполагаемой функции (рис.3.18). При этом можем в качествепримеравыбиратьфункции, расположенныевнижнейчастиокна.
Нажимаем ОК. Потом еще раз ОК.
Рис.3.18. Окно для набора уравнения регрессии
Если нет математической ошибки в наборе функции, то появляется окно (рис.3.19).
Рис. 3.19. Окно выбора процедуры оценивания и установки начальных значений
По нему можно выбрать при необходимости: максимальное значение итераций – Maximum number of iterations, допустимую погрешность –
165
Asymptotic standard errors, стартовое значение факторов – Start values и
настройку размера шага – Initial step size (левая половина) Как правило, можно обойтись без этого. Для предварительной оценки даются медиана и стандартная ошибка; матрица корреляции факторов; интервалы изменения значений факторов (в правом нижнем углу три кнопки). Нажимаем ОК.
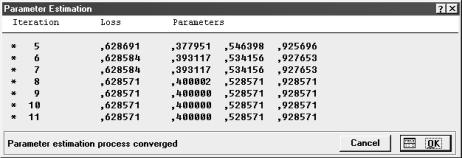
После итерации подбора функций (рис.3.20) должна промелькнуть красная лента и появится надпись Parameter estimation process converged –
Процесс оценки параметров сошелся. Если нет, может быть не подходит уравнение функции. Первая колонка – номера итераций, далее – значения функции потерь, а далее оценки коэффициентов. Увеличение количества итераций при моделировании– нежелательный процесс и симптом низкого качества модели.
Рис. 3.20. Окно итераций подбора коэффициентов функций
Вынуждены повторно нажать ОК. Появляются результаты расчета (рис. 3.21):
Модель: t=а0+а1*s+a2*s*s
Зависимый фактор: Т Независимых факторов: 1
Метод: наименьших квадратов
Финальный остаток: 0,628571429 Доля объясненной дисперсии (мера множествен. определенности): 0,998366498
Множественный коэффициент корреляции: R=0,999182915,
а также кнопки: Левый ряд сверху – Parameter estimates – оценка параметров.
Ранее указанные результаты расчета представлены в виде табл. 3.8. Наличие только численных значений коэффициентов (рис. 3.22 в центре) при отсутствии значений коэффициентов Стьюдента, уровней значимости факторов говорит о том, что данная модель (а скорее матрица для данной модели) не совсем корректна. (Однако иногда применяют и данную модель, используя показатели Быстрых основных статистик). Поэтому придется уточнять исходную функцию. Для этого следует нажать кнопку Cancel и изменить исходную модель.
166
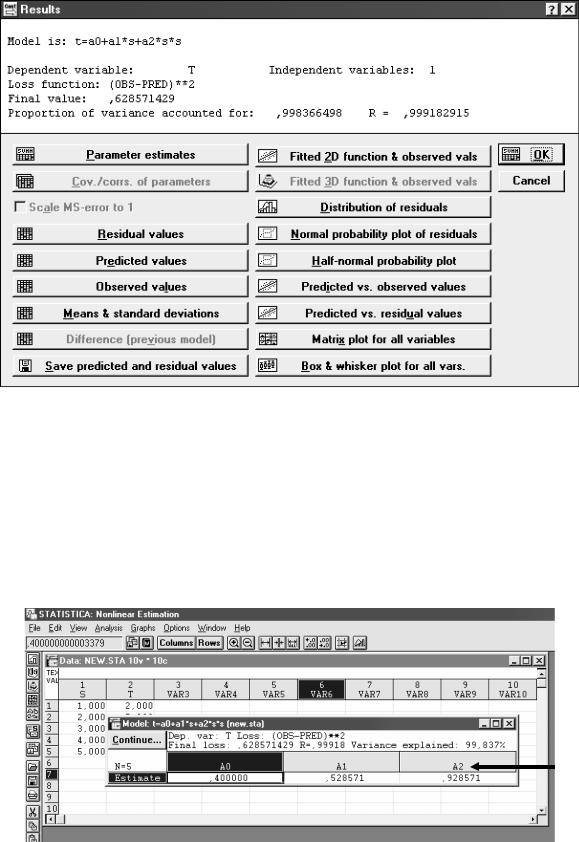
Рис. 3.21. Окно результатов оценивания параметров модели
Таблица 3 . 8
Результаты оценивания
Показатели |
N |
Const А0 |
Const А1 |
Estimate / численное значение коэффициента |
0,004761 |
-7,91822 |
2,074394 |
Std.Err / стандартная ошибка |
0,026792 |
22,12701 |
2,77872 |
t(1) / значение коэф. Стьюдента для 1-й степ.свободы |
0,177694 |
-0,35785 |
0,746529 |
p-level / уровень значимости ошибки фактора |
0,888045 |
0,781223 |
0,591701 |
(желательно не более чем: 1-0,95=0,05) |
|
|
|
Рис.3.22. Окно результатов оценивания параметров модели
Кнопки: Residual values – Результаты расчета значений: разность между опытным и расчетным значением; Predicted values – расчетное зна-
167
чение; Observed values – опытное (исходное) значение. Позволяют оценить сходимость опытных значений и расчетных, полученных по модели. По ним в Excel можно найти F-тест – он возвращает F-распределение вероятности. Используют, чтобы определить, имеют ли обе выборки данных различные степени плотности, т.е. сравнивают их степени разброса. Чем ближе значение F-теста к 1, тем лучше.
Кнопка Means & standard deviations позволяет найти у фактора: mean – среднее; st.dev. – стандартное отклонение; minimum; maximum.
Правый ряд кнопок (сверху)
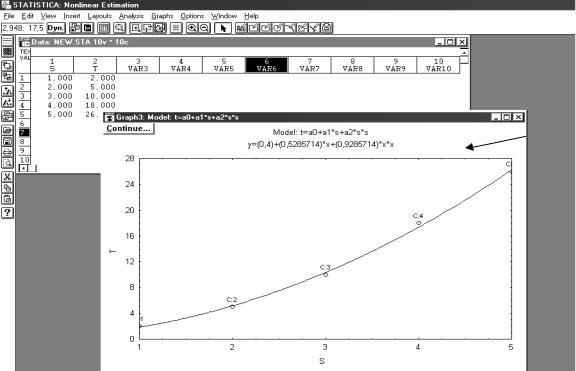
Две верхних – графики (двумерные или трехмерные в зависимости от функции и исходных факторов) с указанием уравнения функции. При числе независимых факторов более двух графики не строятся. В таком случае придется воспользоваться возможностями Mathcad. Для нашего варианта см. рис.3.23. С просмотра данных графиков начинается оценивание моделей.
Рис.3.23. Окно с графическими результатами модели
Порядок редактирования графиков приведен в специальной литературе.
Гистограмма остатков Distribution of residuals (разности между начальными значениями и расчетными значениями) и их соответствие нормальному закону (красная кривая) показаны на рис. 3.24. Чем меньше
168
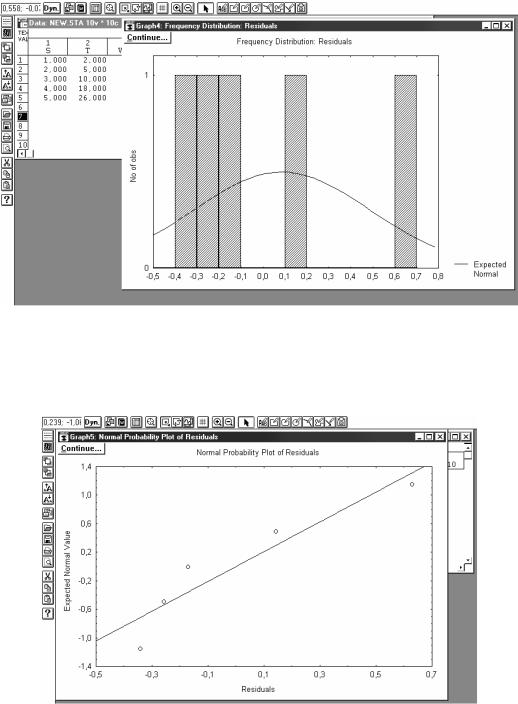
числовой интервал разброса абсолютных значений (у нас от -0,5 до +0,8) и ближе к нормальному закону, тем лучше.
Рис.3.24. Окно с гистограммой остатков модели
Распределение остатков на нормальной бумаге – Normal probaliute – показаны на рис.3.25. Красная линия – нормальный закон.
Рис.3.25. Окно с распределением остатков на нормальной бумаге
Остатки – разности наблюдаемых величин и прогнозируемых моделью. При правильно подогнанной модели они ведут себя хаотически, напоминая белый шум. Данный график аналогичен гистограмме остатков, однако дополнительно дает возможность оценить влияние факторов: случайный ли разброс значений или если что-то не учитывается. У нас видно, что имеется какая-то зависимость (может быть, следует ввести дополнительный член
169
в функцию). Чем ближе значения к красной линии – тем лучше (с учетом абсолютных значений неучтенных остатков).
Когда интересуются лишь абсолютной величиной остатков, используют их график на полунормальной вероятностной бумаге – Half-normal probability plot.
При расхождении исходных данных с моделью либо изменяют критерий сходимости в методе (метод наименьших квадратов на другой), начальный шаг, начальное значение параметров и т.п. в настройках, либо выбирают другой метод оценивания параметров модели Model Estimation, либо переходят к более сложной модели, постепенно усложняя ее.
Кнопку Корреляционные матрицы Matrics plot of residuals (анало-
гично рис. 3.8) используют для предварительного анализа значимости факторов.
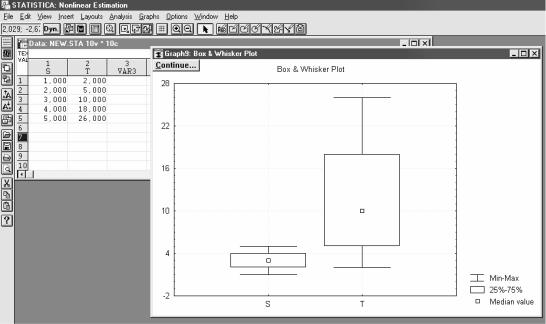
Для оценки разброса значений факторов используются графики на рис.3.26. Они позволяют также визуально оценить соответствие распределений плотности значений исходных и расчетных значений. В нашем случае по ширине размаха и расположению интервалов и медианы явно видна неадекватность показателей.
Рис.3.26. Величины крайних значений и медиана
Аналогична работа с другими модулями.
170
