2074
.pdf
В данном случае придется искать рациональные значения, а при обработке результатов качественных показателей использовать обратные данные (единица, деленная на число) либо подвергнутые логарифмированию.
Model: v=a0+a2*d+a22*d*d+a12*n*d
|
|
|
z=(210,0837)+(-4,3141114)*x+(0,0261)*x*x+(-0,0186674)*y*x |
|
||||||
|
16 |
|
|
|
min=4,8 |
|
|
|
|
|
|
15 |
|
|
|
8 |
|
|
|
|
|
|
14 |
|
|
|
10.3 C:5 |
|
|
|
|
|
8,095 |
13 |
:2 |
|
|
|
|
17.1 |
C |
||
|
|
|
|
|
|
|
||||
10,367 |
|
|
|
|
|
|
|
|
|
|
12,638N |
|
|
17.1 |
|
12.6 |
|
|
|
19.5 |
|
14,909 |
12 |
|
|
|
|
|
|
|
||
17,18 |
|
19.5 |
|
|
|
|
|
21.7 |
|
|
19,451 |
11 |
|
|
|
|
|
|
|||
21,723 |
|
|
|
15 |
|
|
|
|
|
|
23,994 |
|
:3 |
|
|
C:6 |
|
|
24 |
C |
|
26,265 |
10 |
75 |
80 |
85 |
95 |
100 |
||||
28,536 |
70 |
90 |
105 |
110 |
||||||
|
|
|
|
|
|
D |
|
|
|
|
Рис.2.24. Влияние диаметра смесительной камеры D (мм) и частоты |
||||||||||
вращения n (с-1) на неравномерность смешивания компонентов |
||||||||||
|
|
|
(коэффициент вариации), % |
|
|
|
||||
Для описания поверхности отклика используется центральное композиционное планирование, в частности применяя ротатабельные, ортогональные и D-оптимальные планы.
Композиционное планирование отли-
чается равным количеством уровней у разных факторов (рис.2.25).
Для отыскания оптимума у полученной математической модели можно использовать численные методы (например, метод крутого восхождения), иногда методы классического анализа (берутся первые производные по каждой переменной и приравнивают их к нулю, а решение системы всех уравнений позволяет найти экстремум), графический анализдвумернымисечениями.
Нахождение точки выявленного экстремума модели вне исследуемой зоны по плану эксперимента говорит о неправильном нахождении зоны оптимума либо, что чаще, о несоответствии принятой модели реальному процессу (несмотря на статистическую достоверность результата).
Рис. 2.25. Точки факторного пространства, центрального композиционного планирования двухфакторной модели:
– точки ядра плана;
– звёздные точки;
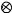– точки в центре плана
131
Планирование эксперимента при описании поверхности отклика полиномом второго порядка получается при добавлении некоторого количества специально расположенных точек к «ядру», образованных планированием для линейного приближения: «звездных» точек, расположенных от центра эксперимента на расстоянии звездного плеча , и центральной точки. Ядром плана может быть и не полный факторный эксперимент, а полуреплика от него. Такое планирование требует меньшего числа опытов, чем полный факторный эксперимент типа 3n. Пример трехфакторного центрального композиционного плана представлен в табл.2.8.
Таблица 2 . 8 Матрица трехфакторного центрального композиционного плана
|
|
|
|
|
|
|
|
|
|
№ п/п |
Х0 |
Х1 |
Х2 |
Х3 |
Х12 |
Х22 |
Х32 |
Y |
|
1 |
+1 |
-1 |
-1 |
-1 |
+1 |
+1 |
+1 |
|
|
2 |
+1 |
+1 |
-1 |
-1 |
+1 |
+1 |
+1 |
|
|
3 |
+1 |
-1 |
+1 |
-1 |
+1 |
+1 |
+1 |
Ядро |
|
4 |
+1 |
+1 |
+1 |
-1 |
+1 |
+1 |
+1 |
||
полнофакторного |
|||||||||
5 |
+1 |
-1 |
-1 |
+1 |
+1 |
+1 |
+1 |
эксперимента |
|
6 |
+1 |
+1 |
-1 |
+1 |
+1 |
+1 |
+1 |
||
|
|||||||||
7 |
+1 |
-1 |
+1 |
+1 |
+1 |
+1 |
+1 |
|
|
8 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
+1 |
|
|
9 |
+1 |
- |
0 |
0 |
|
|
|
|
|
10 |
+1 |
+ |
0 |
0 |
|
|
|
|
|
11 |
+1 |
0 |
- |
0 |
|
|
|
Звездные точки |
|
12 |
+1 |
0 |
+ |
0 |
|
|
|
||
|
|
|
|
||||||
13 |
+1 |
0 |
0 |
- |
|
|
|
|
|
14 |
+1 |
0 |
0 |
+ |
|
|
|
|
|
15 |
+1 |
0 |
0 |
0 |
|
|
|
Нулевая точка |
Широко используются в зависимости от критерия оптимизации ортогональное композиционное планирование и ротатабельное планирование.
План называют ортогональным, если скалярное произведение всех векторов – столбцов матрицы равно нулю. Величина звездного плеча при ортогональном планировании, количество точек куба (гиперкуба-ядра) Nc при полнофакторном эксперименте, число звездных точек N , число точек в центре эксперимента No и общее число точек факторного пространства N для n факторов приведены в табл.2.9. Матрица ортогонального планирования приведена в табл. 2.10. Проверка адекватности описания объекта полиномом 2-го порядка проводится с помощью критерия Фишера. Следует помнить, что точность предсказаний по различным направлениям неодинакова.
132
Таблица 2 . 9 Параметры ортогонального планирования
n |
|
N |
No |
Nc |
N |
2 |
1 |
4 |
1 |
4 |
9 |
3 |
1.215 |
6 |
1 |
8 |
15 |
4 |
1.414 |
8 |
1 |
16 |
25 |
5 |
1.547 |
10 |
1 |
32 |
43 |
Таблица 2 . 1 0 Матрица ортогонального планирования для трех факторов
№ |
|
|
|
|
0,73 |
0,73 |
0,73 |
2 |
3 |
3 |
|
0 |
1 |
2 |
3 |
Х |
Х |
Х |
Примечание |
||||
п/п |
Х |
Х |
Х |
Х |
- |
- |
- |
1 |
1 |
2 |
|
2 |
2 |
2 |
|||||||||
1 |
2 |
3 |
|
||||||||
|
Х |
Х |
Х |
Х |
Х |
Х |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
1 |
0,27 |
0,27 |
0,27 |
1 |
1 |
1 |
|
2 |
1 |
1 |
1 |
-1 |
0,27 |
0,27 |
0,27 |
1 |
-1 |
-1 |
|
3 |
1 |
1 |
-1 |
1 |
0,27 |
0,27 |
0,27 |
-1 |
1 |
-1 |
|
4 |
1 |
1 |
-1 |
-1 |
0,27 |
0,27 |
0,27 |
-1 |
-1 |
1 |
Ядро 23 |
5 |
1 |
-1 |
1 |
1 |
0,27 |
0,27 |
0,27 |
-1 |
-1 |
1 |
|
6 |
1 |
-1 |
1 |
-1 |
0,27 |
0,27 |
0,27 |
-1 |
1 |
-1 |
|
7 |
1 |
-1 |
-1 |
1 |
0,27 |
0,27 |
0,27 |
1 |
-1 |
-1 |
|
8 |
1 |
-1 |
-1 |
-1 |
0,27 |
0,27 |
0,27 |
1 |
1 |
1 |
|
9 |
1 |
-1,215 |
0 |
0 |
0,745 |
-0,73 |
-0,73 |
0 |
0 |
0 |
|
10 |
1 |
1,215 |
0 |
0 |
0,745 |
-0,73 |
-0,73 |
0 |
0 |
0 |
|
11 |
1 |
0 |
-1,215 |
0 |
-0,73 |
0,745 |
-0,73 |
0 |
0 |
0 |
Звездные точки |
12 |
1 |
0 |
1,215 |
0 |
-0,73 |
0,745 |
-0,73 |
0 |
0 |
0 |
|
13 |
1 |
0 |
0 |
-1,215 |
-0,73 |
-0,73 |
0,745 |
0 |
0 |
0 |
|
14 |
1 |
0 |
0 |
1,215 |
-0,73 |
-0,73 |
0,745 |
0 |
0 |
0 |
|
15 |
1 |
0 |
0 |
0 |
-0,73 |
-0,73 |
-0,73 |
0 |
0 |
0 |
Нулевая точка |
Симметричные информационные контуры можно получить с помощью ротатабельного композиционного планирования.
Ротатабельные планы не требуют ортогонализации вектор-столбцов. Все его точки расположены на концентрических гипосферах, число которых не менее двух. Одна из сфер может быть вырожденной – нулевой точкой. Планы, у которых внутренняя дисперсия предсказанного значения постоянна, т.е. не зависит от расстояния до центра плана, называются униформ-планированием. Композиционные центральные ротатабельные униформ-планы (табл.2.11) состоят из трех сфер: центральных точек No, точек куба Nc и звездных точек N . Общее число точек факторного пространства N для n факторов приведено в табл.2.12–2.13.
133
Таблица 2 . 1 1 Данные для построения униформ-ротатабельного плана 2-го порядка
n |
Nc |
No |
N |
|
N |
Примечание |
2 |
4 |
5 |
4 |
1,414 |
13 |
ПФЭ |
3 |
8 |
6 |
6 |
1,682 |
20 |
ПФЭ |
4 |
16 |
7 |
8 |
2,000 |
31 |
ПФЭ |
5 |
32 |
10 |
10 |
2,378 |
52 |
ПФЭ |
5 |
16 |
10 |
6 |
2,000 |
32 |
Полуреплика |
6 |
64 |
12 |
15 |
2,828 |
91 |
Полуреплика |
6 |
32 |
12 |
9 |
2,378 |
53 |
Полуреплика |
7 |
128 |
14 |
21 |
3,333 |
163 |
ПФЭ |
7 |
64 |
14 |
14 |
2,828 |
92 |
Полуреплика |
8 |
256 |
16 |
1 |
4,000 |
273 |
ПФЭ |
8 |
128 |
16 |
1 |
3,333 |
145 |
Полуреплика |
|
|
|
|
|
|
Таблица 2 . 1 2 |
|
|
Данные для построения ротатабельного плана 2-го порядка |
||||||
|
|
|
|
|
|
|
|
n |
|
Nc |
No |
N |
N |
|
Примечание |
2 |
|
4 |
3 |
4 |
11 |
|
ПФЭ |
3 |
|
8 |
2 |
6 |
16 |
|
ПФЭ |
4 |
|
16 |
2 |
8 |
26 |
|
ПФЭ |
5 |
|
32 |
3 |
10 |
45 |
|
ПФЭ |
5 |
|
16 |
1 |
10 |
27 |
|
Полуреплика |
6 |
|
64 |
3 |
12 |
79 |
|
ПФЭ |
6 |
|
32 |
2 |
12 |
46 |
|
Полуреплика |
7 |
|
128 |
1 |
14 |
143 |
|
ПФЭ |
7 |
|
64 |
3 |
14 |
81 |
|
Полуреплика |
8 |
|
256 |
0 |
16 |
272 |
|
ПФЭ |
Таблица 2 . 1 3 Центральное композиционное ротатабельное униформ-планирование
второго порядка
|
|
|
|
|
|
|
№ п/п |
Х0 |
Х1 |
Х2 |
Х3 |
Х4 |
Примечание |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
1 |
1 |
-1 |
-1 |
-1 |
-1 |
|
2 |
1 |
1 |
-1 |
-1 |
-1 |
|
3 |
1 |
-1 |
1 |
-1 |
-1 |
|
4 |
1 |
1 |
1 |
-1 |
-1 |
|
5 |
1 |
-1 |
-1 |
1 |
-1 |
|
6 |
1 |
1 |
-1 |
1 |
-1 |
|
7 |
1 |
-1 |
1 |
1 |
-1 |
|
8 |
1 |
1 |
1 |
1 |
-1 |
Ядро плана 24 |
9 |
1 |
-1 |
-1 |
-1 |
1 |
|
10 |
1 |
1 |
-1 |
-1 |
1 |
|
11 |
1 |
-1 |
1 |
-1 |
1 |
|
12 |
1 |
1 |
1 |
-1 |
1 |
|
13 |
1 |
-1 |
-1 |
1 |
1 |
|
14 |
1 |
1 |
-1 |
1 |
1 |
|
15 |
1 |
-1 |
1 |
1 |
1 |
|
16 |
1 |
1 |
1 |
1 |
1 |
|
134
Окончание табл. 2 . 1 3
1 |
2 |
3 |
4 |
5 |
6 |
7 |
17 |
1 |
-2 |
0 |
0 |
0 |
|
18 |
1 |
2 |
0 |
0 |
0 |
|
19 |
1 |
0 |
-2 |
0 |
0 |
|
20 |
1 |
0 |
2 |
0 |
0 |
Звездные |
21 |
1 |
0 |
0 |
-2 |
0 |
точки |
22 |
1 |
0 |
0 |
2 |
0 |
|
23 |
1 |
0 |
0 |
0 |
-2 |
|
24 |
1 |
0 |
0 |
0 |
2 |
|
25 |
1 |
0 |
0 |
0 |
0 |
|
26 |
1 |
0 |
0 |
0 |
0 |
|
27 |
1 |
0 |
0 |
0 |
0 |
|
28 |
1 |
0 |
0 |
0 |
0 |
Нулевые точки |
29 |
1 |
0 |
0 |
0 |
0 |
|
30 |
1 |
0 |
0 |
0 |
0 |
|
31 |
1 |
0 |
0 |
0 |
0 |
|
D-оптимальные планы. Основаны на теории совместных эффектив- |
|||||||||||
ных оценок, развитой американским математиком Кифером. Они позво- |
|||||||||||
ляют минимизировать обобщенную дисперсию, или объем эллипсоида |
|||||||||||
рассеяния оценок параметров за счет оптимального расположения точек в |
|||||||||||
пространстве факторов. Вторым достоинством является трехуровневое |
|||||||||||
планирование. Это важно при малом количественном значении факторов, |
|||||||||||
когда возможны только целые значения, например при количестве |
|||||||||||
лопастей менее 15. В то время как при ином планировании имеются |
|||||||||||
звездные точки, а соответственно и дополнительные значения – с дробным |
|||||||||||
значением |
факторов, |
при |
трехуров- |
|
|
+1 |
X2 |
|
|
||
невом значении их можно избежать. |
|
|
|
|
|||||||
|
|
|
|
|
|||||||
Некомпозиционное |
|
планирование |
|
5 |
|
3 |
|
|
|||
отличается |
различным |
количеством |
|
|
|
|
|||||
|
|
|
|
|
|
||||||
уровней у разных факторов. Они более |
|
|
|
|
|
|
|||||
эффективны по сравнению с компози- |
-1 |
2 |
|
7,8,9,10 |
1 +1 |
X1 |
|||||
ционными планами, если на основе |
|
|
|
|
|
||||||
априорной информации известно, что |
|
|
|
|
|
|
|||||
рассматриваемый |
процесс |
можно |
|
|
|
|
|
|
|||
описать полиномом второго порядка. |
|
6 |
|
4 |
|
|
|||||
Данный |
план |
для |
двух |
факторов |
|
|
|
-1 |
|
|
|
(рис.2.26) требует проведения десяти |
|
|
|
|
|
||||||
опытов (вместо тринадцати – при ком- |
|
Рис.2.26. Некомпозиционный |
|||||||||
позиционном плане), а кроме того, |
|
ротатабельный план второго |
|
||||||||
один фактор изменяется на трех уров- |
|
порядка для двух факторов |
|
||||||||
нях, а второй – на пяти. |
|
|
|
|
|
|
|
|
|
||
Это немаловажно, когда один из факторов может применять только |
|||||||||||
целые либо определенные значения. Планы для трех, четырех и пяти |
|||||||||||
факторов приведены в приложении. |
|
|
|
|
|
|
|||||
135
Пример 12
Обработка результатов плана оптимизации (листинг программы для Mathcad)
Реализован план оптимизации двухфакторного плана для определения показателей полинома второго порядка.
Максимальный размер матрицы у Mathcad составляет 10х10 ячеек.
В результате парного взаимодействия количество факторов для получения модели
составит: |
|
|
|
|
|
|
n (1 2 1 2) |
1 |
|
n 5 |
|
j 0 n |
||||||||||||||||||
Количество строк в опыте: |
|
|
N 8 |
|
|
|
|
|
|
|
|
|
|
i 1 N |
|
x0 i 1 |
|
|||||||||||||
Матрица плана эксперимента: |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
2 |
|
|
x |
|
2 |
||||||||
x |
1 |
1 |
x |
1 |
1 |
x |
|
1 |
x |
1 |
x |
1 |
x |
|
1 |
|
1 |
x |
1 |
1 |
||||||||||
1 |
|
2 |
|
3 |
|
1 |
|
2 |
|
4 |
|
|
1 |
|
5 |
2 |
|
|||||||||||||
x |
2 |
1 |
x |
2 |
1 |
x |
|
2 |
x |
2 |
x |
2 |
x |
|
2 |
x |
|
2 |
2 |
x |
2 |
x |
2 |
2 |
||||||
1 |
|
2 |
|
3 |
|
1 |
|
2 |
|
4 |
|
|
1 |
|
5 |
2 |
|
|||||||||||||
x |
3 |
1 |
x |
3 |
1 |
x |
|
3 |
x |
3 |
x |
3 |
x |
|
3 |
x |
|
3 |
2 |
x |
3 |
x |
3 |
2 |
||||||
1 |
|
2 |
|
3 |
|
1 |
|
2 |
|
4 |
|
|
1 |
|
5 |
2 |
|
|||||||||||||
x |
4 |
1 |
x |
4 |
1 |
x |
|
4 |
x |
4 |
x |
4 |
x |
|
4 |
x |
|
4 |
2 |
x |
4 |
x |
4 |
2 |
||||||
1 |
|
2 |
|
3 |
|
1 |
|
2 |
|
4 |
|
|
1 |
|
5 |
2 |
|
|||||||||||||
x |
5 |
1 |
x |
5 |
0 |
x |
|
5 |
x |
5 |
x |
5 |
x |
|
5 |
x |
|
5 |
2 |
x |
5 |
x |
5 |
2 |
||||||
1 |
|
2 |
|
3 |
|
1 |
|
2 |
|
4 |
|
|
1 |
|
5 |
2 |
|
|||||||||||||
x |
6 |
1 |
x |
6 |
0 |
x |
|
6 |
x |
6 |
x |
6 |
x |
|
6 |
x |
|
6 |
2 |
x |
6 |
x |
6 |
2 |
||||||
1 |
|
2 |
|
3 |
|
1 |
|
2 |
|
4 |
|
|
1 |
|
5 |
2 |
|
|||||||||||||
x |
7 |
0 |
x |
7 |
1 |
x |
|
7 |
x |
7 |
x |
7 |
x |
|
7 |
x |
|
7 |
2 |
x |
7 |
x |
7 |
2 |
||||||
1 |
|
2 |
|
3 |
|
1 |
|
2 |
|
4 |
|
|
1 |
|
5 |
2 |
|
|||||||||||||
x |
8 |
0 |
x |
8 |
1 |
x |
|
8 |
x |
8 |
x |
8 |
x |
|
8 |
x |
|
8 |
2 |
x |
8 |
x |
8 |
2 |
||||||
1 |
|
2 |
|
3 |
|
1 |
|
2 |
|
4 |
|
|
1 |
|
5 |
2 |
|
|||||||||||||
|
|
|
|
|
|
x0 1 |
x1 1 |
x2 1 x3 1 x4 1 |
x5 1 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
x0 2 |
x1 2 |
x2 2 x3 2 x4 2 |
x5 2 |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
x |
3 |
x |
|
|
x |
3 |
x |
3 |
x |
3 |
x |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
0 |
1 3 |
|
2 |
3 |
|
4 |
|
5 3 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
x |
|
x |
|
|
x |
|
x |
|
|
x |
|
x |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Xx |
0 |
4 |
1 4 |
|
2 |
4 |
3 |
4 |
|
4 |
4 |
|
5 4 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
x0 5 |
x1 5 |
x2 5 x3 5 x4 5 |
x5 5 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
x |
6 |
x |
|
|
x |
6 |
x |
6 |
x |
6 |
x |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
0 |
1 6 |
|
2 |
3 |
|
4 |
|
5 6 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
x0 7 |
x1 7 |
x2 7 |
x3 7 x4 7 |
x5 7 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
x1 8 |
x2 8 |
x3 8 x4 8 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
x0 8 |
x5 8 |
|
|
|
|
|||||||||||||||||||
Количество повторностей опыта: |
|
|
k 3 |
|
|
|
|
jj |
1 3 |
|
|
|
|
|
||||||||||||||||
Результаты проведения опыта: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
y1 1 |
58.5 |
|
y1 2 |
|
64.0 |
|
|
y1 3 |
64.1 |
|
|
|
y1 4 |
62.9 |
|
|
|
|
||||||||||
|
|
y1 5 |
58.0 |
|
y2 1 |
|
59.0 |
|
|
y2 2 |
64.9 |
|
|
|
y2 3 |
65.0 |
|
|
|
|
||||||||||
|
|
y2 4 |
63.8 |
|
y2 5 |
|
59.9 |
|
|
y3 1 |
59.4 |
|
|
|
y3 2 |
64.5 |
|
|
|
|
||||||||||
|
|
y3 3 |
64.8 |
|
y3 4 |
|
63.3 |
|
|
y3 5 |
58.6 |
|
|
|
y1 6 |
69 |
|
|
|
|
||||||||||
|
|
y1 7 |
63.3 |
|
y1 8 |
|
64.8 |
|
|
y2 6 |
69.5 |
|
|
|
y2 7 |
63.0 |
|
|
|
|
||||||||||
|
|
y2 8 |
65.7 |
|
y3 6 |
|
68.6 |
|
|
y3 7 |
63.6 |
|
|
|
y3 8 |
65.2 |
|
|
|
|
||||||||||
136
Среднее значение результата:
Корректированный отклик Yk (см. коррекция в конце) Дисперсия каждого опыта:
S2i |
1 |
|
yjj i Ycpi 2 |
N 1 |
|||
|
|
|
jj |
Наибольшее значение дисперсии: S2max max(S2) S2max 0.27
Количество степеней свободы:
k1 k 1 |
k1 2 |
k2 N 1 |
k2 7 |
|
|
yjj i |
||
Ycp |
jj |
|||
|
|
|
||
|
i |
k |
||
|
|
|||
|
Ycpi |
|
S2i |
|
|
58.967 |
|
0.058 |
|
|
|
|
|
|
|
64.467 |
|
0.058 |
|
|
|
|
|
|
|
64.633 |
|
0.064 |
|
|
|
|
|
|
|
63.333 |
|
0.058 |
|
|
|
|
|
|
|
58.833 |
|
0.27 |
|
|
|
|
|
|
|
69.033 |
|
0.058 |
|
|
|
|
|
|
|
63.3 |
|
0.026 |
|
|
|
|
|
|
|
65.233 |
|
0.058 |
|
|
|
|
|
|
Ycp1 |
|
|
|
|
|
|
|
Ycp2 |
|
|
|
Ycp |
|
|
|
|
3 |
|
|
Ycp |
|
Ykj |
|
Yi |
4 |
|
|
Ycp5 |
|
||
Ycp |
|
|
|
|
6 |
|
|
Ycp7 |
|
|
|
Ycp |
|
|
|
|
8 |
|
|
58.97
64.47
64.6363.33
58.8363.3
65.23
59
Определяемся в потребности коррекции отклика: |
Y Yi |
|||
Значение G-критерия Кохрена: |
G |
S2max |
G 0.415 |
|
S2i |
||||
|
||||
i
Табличное значение критерия Кохрена: Gтабл 0.8010 G Gтабл 1
Поскольку условие оказалось не ложным (равным 1, а не нулю), то гипотезу следует принять (не отвергнуть), то есть мы должны сделать вывод об однородности дисперсий и, следовательно, о достаточной достоверности (воспроизводимости) эксперимента.
S2i
Дисперсия воспроизводимости эксперимента: S2y |
i |
|
N |
||
|
Построение матрицы, транспонированной Хх: Умножим слева матрицу Хх на матрицу Хх': Умножим слева матрицу Хх на матрицу Y:
Обратная матрица Н:
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
1 |
1 |
1 |
1 1 1 |
0 |
0 |
|
|
||
|
|
|
||||||||
|
1 |
1 |
1 1 |
0 |
0 |
1 |
1 |
|
H |
|
Xx' |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
||||||||
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
|
|
|
|
1 |
1 |
1 |
0 |
0 |
1 |
1 |
|
|
1 |
|
|
||||||||
Значения коэффициентов регрессии: |
|
b |
||||||||
Xx' XxT H Xx' Xx Xy Xx' Y
C (Xx' Xx) 1
8 |
0 |
0 |
0 |
6 |
6 |
||
|
0 |
6 |
0 |
0 |
0 |
0 |
|
|
|
||||||
|
0 |
0 |
6 |
0 |
0 |
0 |
|
|
0 |
0 |
0 |
4 |
0 |
0 |
|
|
|
||||||
|
6 |
0 |
0 |
0 |
6 |
4 |
|
|
|
0 |
0 |
0 |
4 |
|
|
6 |
6 |
||||||
(C Xy)
S2y 0.081
|
507.8 |
|
|
14.4 |
|
|
|
|
|
6.467 |
|
Xy |
6.8 |
|
|
|
|
|
379.267 |
|
|
|
|
379.933 |
|
|
137
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
Расчетные значения по уравнению регрессии: Ypi b0 |
xj i b |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
1 |
1 |
1 |
|||
|
65.35 |
|
1.25 |
0 |
0 |
0 |
0.75 |
0.75 |
|
|
|
|
|
|
|
|
|
||
1 |
1 1 |
1 1 1 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
2.4 |
|
|
0 |
0.167 |
0 |
0 |
0 |
0 |
|
|
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
|
||||||||||||||||||
|
1.078 |
|
|
0 |
0 |
0.167 |
0 |
0 |
0 |
|
|
1 |
1 |
1 |
1 |
1 |
1 |
|
|
b |
|
C |
0 |
0 |
0 |
0.25 |
0 |
0 |
|
Xx |
|
||||||||
|
1.7 |
|
|
|
|
1 |
1 |
0 |
0 |
1 |
0 |
|
|||||||
|
1.417 |
|
|
0.75 |
0 |
0 |
0 |
0.75 |
0.25 |
|
|
1 |
1 |
0 |
0 |
1 |
0 |
|
|
|
|
|
|
|
0 |
0 |
0 |
0.25 |
0.75 |
|
|
|
|||||||
1.083 |
|
0.75 |
|
|
1 |
0 |
1 |
0 |
0 |
1 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|||||||
Визуальным анализом сверяем соответствие расчетных и опытных значений (учитывая смещение показателей).
Средние значения результатов: |
|
|
|
0 |
|
|
|
58.97 |
||||||
|
Ypj |
|
|
Yj |
|
57.67 |
|
|
|
64.47 |
|
|||
|
|
|
|
|
|
|
|
|||||||
Ypcp |
j |
|
|
Ycp |
|
j |
|
|
65.87 |
|
|
|
64.63 |
|
N |
1 |
|
N |
|
63.23 |
|
|
|
|
|
||||
|
|
|
|
|
63.33 |
|||||||||
Ypcp 44.705 |
Ycp 47.408 |
|
|
|
|
|
Y |
|
|
|||||
Остаточная сумма квадратов (финальный остаток): |
Yp |
64.63 |
|
58.83 |
|
|||||||||
|
k |
|
|
|
2 |
|
|
|
61.53 |
|
|
|
69.03 |
|
S2R Ypi 1 Yi |
S2R 5.627 |
|
|
|
|
|
|
|||||||
|
|
66.33 |
|
|
|
63.3 |
|
|||||||
|
i 1 |
|
|
|
|
|
|
|
63.19 |
|
|
|
|
|
j 0 n |
|
|
|
|
|
|
|
|
65.34 |
|
|
|
65.23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты ковариации, характеризующие статистическую зависимость факторов:
Сov |
C S2y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсии факторов: |
|
S2bij Cj j S2y |
|
|
|
|
|
|
|
|
|
|
|||
|
0.1 |
0 |
0 |
0 |
0.06 |
|
0.06 |
0.101 |
|
||||||
|
0 |
0.01 |
0 |
0 |
0 |
|
|
0 |
|
|
|
0.014 |
|
||
|
|
|
|
|
|
|
|||||||||
|
0 |
0 |
0.01 |
0 |
0 |
|
|
0 |
|
|
|
0.014 |
|
||
Сov |
0 |
0 |
0 |
0.02 |
0 |
|
|
0 |
|
|
S2bi |
0.02 |
|
||
|
|
|
|
|
|
|
|||||||||
|
0.06 |
0 |
0 |
0 |
0.06 |
|
0.02 |
|
|
0.061 |
|
||||
|
|
0 |
0 |
0 |
0.02 |
|
0.06 |
|
|
|
|
||||
0.06 |
|
|
0.061 |
|
|||||||||||
Ошибка коэффициентов регрессии: |
Sbi |
|
|
S2bi |
|
|
|
|
|||||||
|
|
N n |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Значения t-критерия для коэффициентов: tj |
|
bj |
|
|
|
|
|
|
|||||||
Sbij |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Уровень критерия проверки гипотезы (значимости ошибки): |
0.05 |
|
|||||||||||||
Количество степеней свободы: |
1 n 1 |
|
|
|
|
|
|
|
|
|
|
||||
138
Квантиль распределения Стьюдента: |
|
|
|
|
|
|
1 |
|
|
|
T 2.776 |
T qt |
2 |
1 |
|||
|
|
|
|
|
|
Проводим проверку значимости |
коэффициентов |
|
1.297 10 |
3 |
0.05 |
|
|||||
регрессии. Незначимые коэффициенты принимаем |
|
|
|
0.018 |
|
||||||
равными нулю: |
|
|
|
|
|
130.486 |
|
|
|
||
to 0 bj |
to |
if T |
|
tj |
|
|
58.598 |
|
|
0.018 |
|
|
bj |
otherwise |
t |
|
Sbi |
0.023 |
|
||||
|
|
75.467 |
|
|
|
||||||
Число значимых коэффициентов в уравнении: |
|
36.309 |
|
|
0.039 |
|
|||||
n 1 6 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
27.766 |
|
0.039 |
|
|
Дисперсия отклонения результатов расчета от опытов:
S2ад |
S2R |
S2ад 2.8134 |
N (n 1) |
Доверительный интервал для коэффициентов регрессии c 95 %-й вероятностью:
Число степеней свободы: |
bj |
tj S2y N 1 |
|
|
|
|
|
||
2 N 1 |
2 |
7 |
|
|
|
|
|
||
F-критерий Фишера: |
|
|
|
13.167 |
|
65.35 |
|
||
S0 S2ад |
S1 S2y |
|
|
1.324 |
|
|
2.4 |
|
|
|
|
|
|
|
|||||
max(S) |
|
|
|
0.595 |
|
|
1.078 |
|
|
F min(S) |
F 34.652 |
|
b |
|
b |
|
|||
Критическое значение F-критерия Фишера: |
|
0.766 |
|
|
1.7 |
|
|||
|
0.368 |
|
|
1.417 |
|
||||
Fkp qF 1 1 2 |
Fkp 4.12 |
|
|||||||
|
|
|
|
|
|
|
|||
F Fkp 0 |
|
|
0.282 |
|
1.083 |
|
|||
Поскольку условие оказалось ложным (равным нулю, а не 1), то гипотезу следует отвергнуть (не принять), то есть мы должны сделать вывод о неравноточности или неравнорассеянности дисперсий (различия представленных выборок значимы), значит, полученная модель неадекватно описывает результаты опытов и следует перейти к модели более высокого порядка.
При адекватной модели определяют скорректированные средние квадратичные отклонения результатов:
|
|
1 |
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
2 |
||||
Sx |
|
Ypcp Ypi |
|
Sy |
Ycp Ycpi |
||||||||||||
N 1 |
|
|
|
N 1 |
|
|
|||||||||||
Sx 20.266 |
i 1 |
|
|
|
Sy 17.498 |
i |
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||
Выборочный корреляционный момент: |
|
|
|
|
|
|
|
|
|
|
|
||||||
Kxy |
1 |
|
Ycp Ycpi Ypcp Ypi |
Kxy 352.704 |
|
|
|||||||||||
N 1 |
|
|
|||||||||||||||
|
|
|
|
i |
|
|
|
Kxy |
|
|
|
|
|
|
|||
Коэффициент корреляции: |
|
|
r |
|
|
r 0.9946 |
|||||||||||
|
|
Sy Sx |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Корреляционное отношение: |
|
|
|
|
|
|
|
|
S2ад |
|
0.167 |
||||||
|
|
|
|
1 S2y S2ад |
|||||||||||||
|
|
|
|
|
|
|
|
||||||||||
Множественная мера определенности: |
r2 0.989 |
|
|
|
|
|
|||||||||||
139
t-критерий коэффициента корреляции: tr |
|
r |
N 2 |
|
|
tr 23.492 |
||||||
|
|
|
1 r2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
Табличное значение t-критерия: Tr qt |
1 |
|
n 1 1 |
Tr |
2.571 |
|
tr |
|
Tr 0 |
|||
|
|
|||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Поскольку условие оказалось ложным (равным нулю, а не 1), то мы должны сделать вывод о существенности различий в представленных выборках, то есть вычисленное значение коэффициента корреляции достоверно.
Корректировка результатов
Коэффициент, значение которого недостоверно (например, b1): b1 2.4
Представим матрицу Хх в виде векторов: |
|
|
|
|
|
|||
|
X0 Xx 0 |
X1 Xx 1 |
X2 Xx 2 |
X3 Xx 3 |
X4 Xx 4 |
X5 Xx 5 |
||
|
|
|
|
|
|
|
|
|
Снимаем действие эффекта первого (данного b1) фактора для значений Xxi=+1: |
||||||||
|
Ykk1j Yj b1 |
Xb1 X1 |
Y'j |
|
Ykk1jif Xb1j |
0 |
||
|
|
|||||||
|
|
|
|
|
|
|
|
|
Ypcs d b0 b1 Xs b2 Zd b3 Xs Zd b4 Xs 2 b5 Zd 2
Полученные значения Y'j сравним с ранее принятыми результатами Yj.
Осуществим графический анализ (рис. 2.27) полученного уравнения регрессии. Перейдем к координатам X и Z, для этого введем векторизацию:
|
s 0 11 |
d 0 10 |
|
Xs |
1.2 0.2 s |
Zd 1 |
0.2 d |
Y'j |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
61.367 |
|
0 |
58.967 |
|
|
|
|
|
|
|
1 |
64.467 |
|
|
1 |
|
|
64.467 |
|
|
|
|||||
Y |
|
|
1 |
|
|
|||
|
|
|
|
|
|
|
||
|
|
|
|
|
||||
67.033 |
j |
2 |
64.633 |
Xb1 |
|
1 |
|
|
|
|
3 |
63.333 |
|
|
|||
63.333 |
|
|
|
1 |
|
|
||
|
|
4 |
58.833 |
|
|
|
|
|
61.233 |
|
|
|
|||||
|
|
|
0 |
|
|
|||
|
|
|
|
|
|
|||
69.033 |
|
5 |
69.033 |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
Построим трехмерный график Ypc: по горизонтали координата Х,
по вертикали координата Z (рис. 2.28).
В некоторых версиях Matchcad происходит смещение координатной сетки (вместо от -1 до +1 к участку от 0 до 10) при сохранении надлежащих числовых значений Ypc. Анализ полученного графика позволяет сделать вывод, что имеется экстремум в районе Х=-1 и Z=+5. Однако маловероятно, что экстремальное значение находится в плане эксперимента. Скорее всего, придется проводить дополнительные мероприятия по определению или уточнению месторасположения оптимума. Получаемые при этом значения включаются в план-матрицу эксперимента.
140