Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2074

.pdf

Скачиваний:

Добавлен:

16.06.2024

Размер:

4.62 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 4011 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

планирования экспериментов используются и средние значения уровня факторов (0).

Имеется возможность варьирования (изменения значений) сразу несколькими, а не одним фактором, что также сокращает объем экспериментальной работы без потери точности. Факторный эксперимент позволяет выявить значимость действия факторов. При этом эффект фактора – изменение отклика при изменении уровня данного фактора.

Если число исследуемых факторов не превышает трех, то применяют полный факторный эксперимент. При числе факторов от трех до пятнадцати используют дробные реплики. Когда количество факторов превышает 15, то осуществляется ранжирование (выявление значимости) факторов. Несущественные факторы отсеивают. Для этого используют априорный отсев факторов (на основе проведенных теоретических исследований, данных литературных источников, по аналогии с подобными системами и т.п.), априорное ранжирование факторов, иногда отсеивающий эксперимент. При этом у малозначащих факторов, отсеиваемых для дальнейших экспериментов, определяют их рациональное значение.

Нередко предварительно проводятся небольшие серии опытов для отыскания месторасположения области оптимума. При этом желательно двигаться наиболее коротким путем, например – методом восхождения по поверхности отклика в направлении градиента, под которым понимают наибольшую скорость изменения функции.

Участок, на котором значение функции почти не меняется (почти горизонтальная область) используется для реализации оптимальных планов (заключительный этап факторного планирования).

При выборе количества факторов для реализации планов эксперимента следует не забывать, что при росте числа факторов повышается вероятность расхождения существующих тенденций, наблюдающихся в получаемой модели и у реального процесса.

Причина такого расхождения объясняется несовершенством полученной трехфакторной математической модели. Дело в том, что математическая модель фактически не описывает реальный исследуемый процесс, а стремится пройти через опытные точки плана эксперимента. Это связано с тем, что в процессе же получения математической модели осуществляется подбор числовых значений коэффициентов регрессии выбранной функции, обеспечивающих максимальное приближение расчетных значений отклика к опытным данным в точках плана эксперимента. В связи с наличием аналогичных фактов полученные модели должны подвергаться не только статистическому, но и графическому, и логическому анализу.

101

Полученные опытные значения отклика представляются в виде некоторой математической функции (модели), описывающей его (отклика) поверхность (см. регрессионный анализ), анализируя уже которую находят оптимум (экстремум функции-модели), а после этого проводят экспериментальную проверку истинности полученного экстремума.

В качестве критерия оптимизации можно использовать экономический показатель, выход продукта, энергозатраты и т.п., главное, чтобы критерий имел ясный физический смысл и количественную оценку, а его выбор был должным образом обоснован. Иногда используется один критерий оптимизации и дополнительно осуществляется решение интерполяционной задачи для определения влияния факторов на ряд дополнительных показателей, играющих роль ограничений (например, степень выхода продукции из сырья – критерий оптимизации, а производительность оборудования, энергоемкость процесса и качество продукции – ограничения, характеризующие рабочий процесс). Иногда используют несколько критериев оптимизации – в этом случае требуется решить комплексную задачу. В общем случае выбор критерия оптимизации определяется конкретными особенностями объекта исследования, его физической природой, возможностями экспериментальной установки и интуицией исследователя.

Данный параметр должен обладать простым и ясным физическим смыслом, не зависеть от времени, быть эффективным с точки достижения поставленной цели, универсальным и всесторонне отражать свойства процесса, обладать количественной оценкой и отражаться числом (пусть даже баллами), быть статистически эффективным (иметь наименьшую при данных условиях дисперсию).

Прочие характеристики процесса (количественные, качественные и энергетические показатели) выступают как ограничения. Регистрация указанных данных в проводимых опытах позволит получить более объемную, красочную картину протекания исследуемого процесса. Анализ характера их изменения, наряду с критерием оптимизации, может оказаться полезным при решении ряда практических задач, а также позволит выявить (а иногда подтвердить) существующие внутренние тенденции.

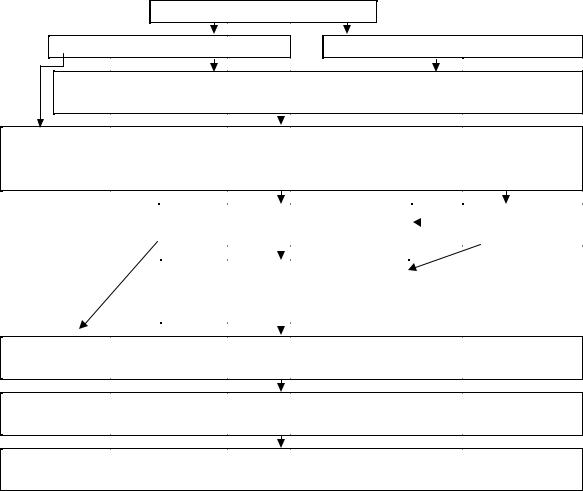
Желательно, чтобы отсеивающий эксперимент был проведен в тех же интервалах варьирования факторов, что и планы по оптимизации значений отклика. В противном случае нельзя будет утверждать, что значимость факторов сохранилась. Наиболее распространенные варианты реализации экспериментов приведены на рис.2.18.

102

Факторы

Априорныйотсевфакторов

Априорноеранжированиефакторов

Проведениелабораторныхипоисковыхисследованийповыявлению рациональныхзначенийрядафакторов

Определениезоныработоспособностиопытногообразца. Поисковыеопытыпо определениюориентировочногоместорасположениязоныоптимизации, натуральныхзначенийуровнейиинтервалаварьированияфакторов

	Полнофакторныйэксперимент					Отсеивающий
	илиегодробныереплики					эксперимент


	Методкрутоговосхождения
	(движенияпоградиенту)
	впоискезоныоптимизации

Реализацияпланаоптимизации. Получениефункциональноймодели. Поископтимальныхзначений

Проверкаоптимальностивыбранныхзначений. Уточнениефункциональнойзависимости

Производственнаяпроверкавыбранныхзначений. Получениетехнической характеристикиустройствапонормативнымиобщепринятымпараметрам

Рис.2.18. Общая схема проведения эксперимента при факторном планировании

Априорное ранжирование факторов (психологический эксперимент) –

формализация разрозненных сведений об изучаемом объекте, позволяющая сравнить различные факторы между собой для решения экспериментальной задачи. Суть данного метода сводится к следующему: что исследователям из различных научных школ предлагается расположить факторы, действующие в объекте, в порядке убывания величины вносимого ими вклада или влияния на критерий оптимизации, т.е. требуется проранжировать n потенциально возможныхфакторов, присвоивимпорядковыеномера(ранги): 1, 2, 3…n.

Каждому специалисту при опросе предлагается заполнить анкету с указанием предполагаемых факторов, их размерности и предполагаемых интервалов варьирования. Специалист назначает место каждого фактора, а также может дополнить анкету новыми факторами или изменить интервал варьирования. Количествоучастниковопросадолжнобытьповозможностимаксимальным.

103

По результатам опроса вычисляется коэффициент конкордации W (согласования), определяющий степень согласованности мнений специалистов:

W		12 S					,
W	m2 (n3 n)						,
где m – количество опрашиваемых специалистов;
n – количество факторов;
S – сумма квадратов отклонений:
n		m
S ( ai, j L)2 ,
i 1		j 1
здесь аi,j – ранг (порядковый номер				при			опросе)	i-го фактора у j-го
специалиста;
L – среднее значение сумм рангов по каждому фактору:
		n	m
		ai, j
L		i 1	j 1			.
L			n			.
			n
При наличии связанных рангов: W							S		.
При наличии связанных рангов: W					( 112) m2 (n3			m	.
					( 112) m2 (n3			n) m Ti
								j 1

Чем ближе к 1 значение W (или далее от 0), тем больше согласованность мнений у специалистов. Если специалист не может решить, кому отдать предпочтение – второму или третьему фактору, то каждому из них приписывается значение2,5. Данныефакторыобладаютсвязаннымирангами.

Проверка значимости коэффициента конкордации проводится по критерию 2:

2 W m (n 1) ( 112) mSn (n 1) .

Или для связанных рангов:

				2	S			,
				2		1		,
				( 1	) m n (n 1)	1	T
				( 1	) m n (n 1)	n 1	T
				12		n 1	i
		1	m
где Ti		1	(t 3j	t j ) ;
где Ti	12		(t 3j	t j ) ;
	12		j 1

tj – j-е количество одинаковых рангов в j-м ранжировании.

104

Если значение распределения больше табличного при соответствующем числе степеней свободы, то коэффициент конкордации значимо отличается от нуля и можно утверждать, что согласованность исследователей не является случайной.

Пример 8

Обработка результатов ранжирования факторов (листинг программы для Mathcad)

Количество факторов:		n 15		i	0 n 1
Количество опрошенных специалистов: m					10 j		0 m
Матрица плана опроса:
	8		7		9
	7		6			8
	7		6			8
	4		4			4
	1		3			1

	2		2		3
3		1			2
	5		5		2		a3
a0	6	a1	8	a2		6	a3
	9		10			7
	12		9			10
	12		9			10
	11		11			11
	10		12			12
	10		12			12
	13		14		13
	14		13			5

	15		15			14

412368710

9121115

1314

	14
	11
	11
	9
	6

	5
	4
	3
	3
a4	1
	2
	7
	7
	8
	10
	10
12
	13

	15

105

13		11		8		7		7
	11		10		10		8		8
	11		10		10		8		8
	6		3		7		6		6
	5		2		2		5		5

4		4		5		4		2
3		5		6		3		15
1		6		1		2		4
a5	2	a6	1	a7	4	a8	9	a9	3
	7		7		3		10		9
	8		8		9		1		8
	8		8		9		1		8
	9		9		11		12		10
	10		13		13		11		14
	10		13		13		11		14
	12		12		12		13		11
	15		14		14		15		12

	14		15		15		14		13

Количество связанных рангов, указанных каждым специалистом:

t0 0

t1 0

t2 2

t3 0

t4 0

t5 0

t6 0

t7 0

t8 0

t9 0

Среднее значение сумм рангов по каждому фактору:

a0i

a1i

a2i

a3i

a4i

a5i

a6i

a7i

a8i

a9i

Сумма квадратов квадратичных отклонений:

S1 a0i L0 2 a1i L1 2 a2i L2 2 a3i L3 2

S2 a4i L4 2 a5i L5 2 a6i L6 2 a7i L7 2

S3 a8i L8 2 a9i L9 2

S S1 S2 S3

S 2723.467

106

Коэффициент связанности факторов:

T 0.5

Коэффициент конкордации (согласования):

W 0.0973

m2 n3 n 12 1

при наличии связанных рангов:

W1 0.0973

12 1 m2 n3 n m T

Критерий 2:

14.111

12 1 m n (n 1)

(n 1) T

Уровень критерия проверки гипотезы (значимости ошибки): 0.05 Критическое значение 2 - критерия Пирсона, соответствующее уровню значимости ошибки 0.05 и числу степеней свободы m (n 1) 140

2т	qchisq		m (n 1)	2т 109.137
		2

2 2т 1

Поскольку 2 меньше табличного значения (неравенство равно единице), поэтому различия между сравниваемыми распределениями не существенны, а отклонения носят случайный характер.

Усредненное значение рангов:

Ai a0i a1i a2i a3i a4i a5i a6i a7i a8i a9i

Строим диаграмму рассеяния значений. Выбираем двумерный график и задаем тип линии bar (рис. 2.19).

150													0
150												0	89
												0	89
												1	83

												2	50
												2	50
100												3	32
												3	32
												4	34
												4	34

Ai												5	48
												5	48
											A	6	37


50												7	47
												8	74
												9	81
												9	81
												10	104
0												11	116
												11	116
		0	2	4	6	8		10	12	14
		0	2	4	6	8		10	12	14		12	127
												12	127
							i					13	128
	Рис. 2.19. Диаграмма усредненного значения рангов											14	144

107

Ранжирование факторов по их значимости (рис. 2.20): Ayi max(A) A

120

	100



Ayi	80
	80
	60


	40


	20


	0

		0	2	4	6	8		10	12	14
							i

Рис. 2.20. Диаграмма значимости факторов

Большая высота ранга говорит о преимущественности выбора фактора. Так, по мнению специалистов, наибольшее предпочтение отдается 3, 4 и 6 факторам.

Построим статистический ряд, расположив информацию в порядке возрастания данных

с помощью функции sort (рис. 2.21).						Ay sort(Ay)
120
120
100



80
80
	Ayi 60



40
40
20


0

		0	2	4	6		8		10	12	14
								i
			Рис. 2.21. Диаграмма значимости факторов

108

По результатам расчета строится диаграмма рангов факторов, отражающая коллективное мнение специалистов. В случае неравномерного убывания диаграммы (наподобие экспоненты) – для дальнейших опытов отбирают небольшую часть наиболее «главных» факторов, а остальные исключают. При монотонном убывании следует включать в дальнейшие опыты по возможности большее количество факторов.

Метод случайного баланса (отсеивающий эксперимент) используется для выявления влияния отдельных факторов и исключения в последующих опытах малозначащих факторов. Он проводится с целью сокращения последующего количества проводимых опытов. Не следует забывать, что при отсеивающих экспериментах дается грубая, приближенная оценка влияния факторов. Поэтому при сомнении относительно влияния какоголибо фактора желательно все же включить его в последующий план опытов, а не отбросить.

Вначале проводят серию опытов по специальной матрице (взяв случайное сочетание уровней факторов «+» и «–» либо используя случайное смешивание двух полуреплик), а затем строят диаграммы рассеяния для визуальной оценки, влияния того или иного фактора для количественной оценки. В первой половине списка факторов стараются поместить наиболее значимые факторы по априорному ранжированию для построения первой полуреплики, во вторую полуреплику включают оставшиеся факторы, распределяя их значения случайным образом. Матрица считается пригодной (табл. 2.3), если в ней нет двух однотипных столбцов (с одинаковыми или неодинаковыми знаками). Наличие столбцов с одинаковыми знаками не позволит различить их эффекты. Также должны отсутствовать столбцы, скалярное произведение которых на любой другой столбец дает столбцы из одинаковых знаков (+ или –). Записывают также значения отклика по повторностям и среднее значение. Обязательной строкой (для контроля линейности модели) является наличие значений факторов в центре интервала варьирования, т.е. при значениях уровней, равных нулю.

Для анализа результатов строят диаграммы рассеяния. Для этого по оси абсцисс наносят все факторы с их уровнями, а по оси ординат – опытные значения критерия оптимизации (отклика). Каждый фактор и его уровень подразделяют на группы, а для каждого из них в отдельности указывают величину отклика. Степень влияния того или иного фактора оценивают визуально (либо в цифровой величине) по значению разности между средними значениями критерия оптимизации, вычисленного для каждого уровня фактора.

109

Таблица 2 . 3

Матрица отсеивающего эксперимента

№

Факторы

п/п

Х1

Х2

Х3

Х4

Х5

Х6

Х7

Х8

–

В качестве среднего значения отклика для одного уровня принимается медиана (использование среднего арифметического значения в инженерных исследованиях может привести к абсурду). Учитывается также количество «выделяющихся» точек.

Для каждого фактора определяется величина эффектов и проверяется их значимость по t-критерию. Вычисленное значение критерия должно быть больше табличного.

После выделения нескольких эффектов производится корректировка результатов для выделения эффектов менее сильных факторов и их взаимодействий. Для этого прибавляем с обратным знаком эффекты выделенных факторов к результатам отсеивающих экспериментов. Факторы бывают иногда незначимы, но оказываются сильны их парные взаимодействия.

Часто встречается случай, когда часть факторов значима, а часть нет. Если данный фактор включался в план из осторожности, то его можно отсеять. Обычно же расширяют интервал варьирования в следующей серии опытов. При повторении результата – фактор можно отсеять. Иногда, когда нельзя расширить интервалы варьирования факторов, рекомендуется многократное повторение той же серии эксперимента, что позволяет при статистическом усреднении выделить значимые коэффициенты.

110

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 1011 / 4011 12 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.06.2024227.61 Кб0207.pdf
#
16.06.20244.6 Mб12070.pdf
#
16.06.20244.61 Mб12071.pdf
#
16.06.20244.62 Mб12072.pdf
#
16.06.20244.62 Mб02073.pdf
#
16.06.20244.62 Mб12074.pdf
#
16.06.20244.63 Mб02075.pdf
#
16.06.20244.64 Mб02076.pdf
#
16.06.20244.65 Mб02077.pdf
#
16.06.20244.67 Mб02078.pdf
#
16.06.20244.68 Mб22079.pdf

13		11		8		7		7
	11		10		10		8		8
	11		10		10		8		8
	6		3		7		6		6
	5		2		2		5		5

4		4		5		4		2
3		5		6		3		15
1		6		1		2		4
a5	2	a6	1	a7	4	a8	9	a9	3
	7		7		3		10		9
	8		8		9		1		8
	8		8		9		1		8
	9		9		11		12		10
	10		13		13		11		14
	10		13		13		11		14
	12		12		12		13		11
	15		14		14		15		12

	14		15		15		14		13

13		11		8		7		7
	11		10		10		8		8
	11		10		10		8		8
	6		3		7		6		6
	5		2		2		5		5

4		4		5		4		2
3		5		6		3		15
1		6		1		2		4
a5	2	a6	1	a7	4	a8	9	a9	3
	7		7		3		10		9
	8		8		9		1		8
	8		8		9		1		8
	9		9		11		12		10
	10		13		13		11		14
	10		13		13		11		14
	12		12		12		13		11
	15		14		14		15		12

	14		15		15		14		13

13		11		8		7		7
	11		10		10		8		8
	11		10		10		8		8
	6		3		7		6		6
	5		2		2		5		5

4		4		5		4		2
3		5		6		3		15
1		6		1		2		4
a5	2	a6	1	a7	4	a8	9	a9	3
	7		7		3		10		9
	8		8		9		1		8
	8		8		9		1		8
	9		9		11		12		10
	10		13		13		11		14
	10		13		13		11		14
	12		12		12		13		11
	15		14		14		15		12

	14		15		15		14		13