
2074
.pdf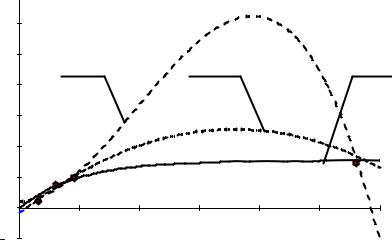
Однако это не соответствует действительности. Более реальна экспоненциальная модель. С увеличением высоты столба материала масса уравновешивающего груза асимптотически приближается к некоторой величине. Тем более, что данная модель хорошо согласуется с теоретическими положениями. Поэтому, как правило, получаемые эмпирические зависимости справедливы только на исследуемых участках факторов. Использование экстраполяции (переноса зависимостей за пределы значений аргумента) весьма ограничено.
|
120 |
|
|
|
|
|
|
|
100 |
a |
|
|
б |
|
в |
|
|
|
|
|
|||
Р |
80 |
|
|
|
|
|
|
|
60 |
|
|
|
|
|
|
|
40 |
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
0 |
50 |
100 |
150 |
200 |
250 |
300 |
|
20 |
|
|
Н |
|
|
|
Рис.2.14. Влияние высоты столба материала Н на давление Р: полином третьего порядка (а), второго порядка (б) и экспоненциальная модель (в)
Экстраполяция – метод, при котором принимается, что развитие процесса во времени или изменение показателя с изменением основного параметра будут изменяться в соответствии с полученной зависимостью.
2.3.2. Методики проведения экспериментальных исследований
Планирование эксперимента – это процедура выбора числа и условий проведения опытов, необходимых и достаточных для решения поставленной задачи с требуемой точностью. Необходима разработка такой стратегии планирования эксперимента, которая позволила бы, проводя минимальное число опытов при одновременном варьировании всеми факторами, получить необходимые данные как для выявления искомых зависимостей, так и для определения оптимального (или по крайней мере рационального) значения конструктивнотехнологических параметров исследуемого процесса.
Входные воздействия в процессе проведения эксперимента принято называть факторами (независимыми переменными), а реакцию на них –
откликом (зависимой переменной). Значения отклика характеризуются изменением (приращением) соответствующего выходного показателя. Данный параметр подлежит оптимизации, и его называют параметром
91
оптимизации. Уравнение, связывающее параметр оптимизации с факторами, называют функцией отклика, а геометрическое ее представление – поверхностью отклика. Топографическое изображение поверхности отклика осуществляют линиями равного выхода, каждая из которых соответствует определенному значению параметра отклика.
Факторы бывают количественные и качественные. Качественные факторы– различные вещества, технологические способы, типы рабочих органов. Если фактор можно оценить количественно (взвесить, замерить и т.п.), то его называют количественным. Фактор должен быть управляемым – в процессе опыта иметь постоянное значение или изменяться по соответствующему закону.
Числовые значения исследуемых факторов называют уровнем фактора. Как правило, в опытах для упрощения и удобства обозначения и облегчения ручной обработки результатов вводят кодированные значения факторов, при этом минимальное значение фактора условно принимают равным «–1», максимальное значение принимают «+1». Иногда используют и промежуточные значения.
Величина изменения числовых значений фактора от минимальных до максимальных исследуемых значений называется интервалом варьирования. Интервал изменения численных значений факторов между соседними уровнями называется шагом варьирования. Интервал варьирования фактора должен быть больше удвоенной среднеквадратической ошибки его определения. Используют узкие (при сильно выраженной кривизне отклика), средние и широкие интервалы варьирования факторов (при низкой точности фиксирования факторов, малой кривизне поверхности отклика, узком диапазоне изменения интервала).
Ориентировочно можно считать, что узкие интервалы варьирования факторов должны составлять не более 10 % от интервала изменения соответствующих факторов, а средние – не более 30 %.
Современные компьютерные технологии позволяют обрабатывать опытные данные и получать функциональные зависимости как при использовании кодированных, так и натуральных значений факторов.
Используемая лабораторная установка должна позволять экспериментатору придавать каждому фактору любое возможное значение в пределах выбранного интервала и поддерживать или изменять по заданному закону его (значение) до конца опыта.
Проводимые опыты могут быть как пассивными, так и активными. При пассивном наблюдении исследователь лишь регистрирует раз-
личные интересующие его стороны развития явления. Для регистрации используют самые разнообразные средства измерений и отметок. Пассивное наблюдение можно чередовать (во времени) с активным (экспериментом, опытом). Наблюдение становится активным, когда исследователь
92
сам определяет условия развития явления и видоизменяет эти условия в желаемом направлении для получения ясных закономерностей.
При планировании эксперимента широко используются методы подобия и размерностей; построение математических моделей; планирование эксперимента. Например, проводится экспериментальное исследование лабораторной установки с малыми габаритами, а результаты используются в производстве на агрегате, имеющем большие габариты. При этом дополнительно уточняется величина поправочного коэффициента.
Первой ступенью активного наблюдения являются поисковые опыты. Их проводятнестолькодляраскрытияимеющихсязакономерностей, сколько:
–для проверки отдельных частей разработанной методики и приспособленности приборов к предполагаемым замерам;
–для обоснования количества замеров в опытах;
–для проверки общей работоспособности исследуемого опытного образца устройства с одновременным ориентировочным выявлением уровней и интервала изменения ряда факторов;
–для проверки варианта рабочей гипотезы и выбора направления элементов исследований с целью сокращения общего количества опытов (например, выбор типа рабочего органа).
Проводиться они могут как на лабораторных установках, так и непосредственно на опытном образце.
Если проверяют направление процесса, то обычно достаточно двух опытов. Если устанавливают, какие факторы обусловливают развитие явления, то минимальное количество опытов – удвоенное количество изучаемых факторов. При более детальном изучении фактора ставится небольшая серия (3–5) опытов.
При проведении экспериментальных исследований наибольшее распространение получили традиционные (классические) планы проведения эксперимента и теория факторного эксперимента. Каждый из вариантов имеет свои положительные и отрицательные моменты.
При этом задачи, решаемые в процессе исследований, бывают интерполяционные (только для выявления существующих связей между факторами и откликом) и экстремальные (когда требуется найти условия, при которых отклик, он же параметр оптимизации, достигает экстремального значения: максимума или минимума).
С целью устранения ошибок, при проведении опыта проводят рандомизацию – чередование опытов (сочетание значений – уровней факторов)
вслучайном порядке, по жеребьевке или по таблицам случайных чисел таким образом, чтобы в процессе опытов постоянно изменялось значение уровня конкретного фактора (по строкам плана). В случае отсутствия проведения рандомизации по экономическим или иным причинам, она может не проводиться. Однако это неизбежно скажется на точности полу-
93
чаемого результата. Чем меньше влияние фактора, тем больше положительное влияние рандомизации. В случае проведения опытов на нескольких машинах следует помнить, что если рандомизированный план и усредняет эффекты воздействия от конкретных особенностей машин, то не устраняет разницы между машинами.
При классическом планировании всем независимым переменным (факторам), кроме одной, придается постоянное значение. Переменную изменяют, придавая различные значения (варьируя уровень) во всем интервале изменений, а по результатам эксперимента находят функциональную зависимость (пример 7). Затем придают различные значения следующей переменной при постоянстве других факторов и также находят функциональную зависимость. Аналогично поступают со всеми независимыми переменными. По результатам проделанной работы устанавливают функциональную зависимость от всех независимых переменных.
Многофакторные эксперименты при классическом планировании проводятся также, как и однофакторные. Число факторов, как правило, небольшое (чаще всего до трех).
Недостатком указанной методики является высокая трудоемкость проведения экспериментальных работ. Положительный момент – четко прослеживаются имеющиеся тенденции изменения отклика.
Пример 7
Обработка результатов однофакторного плана и нахождение экстремума (листинг программы для Mathcad)
В результате проведения опытов известны исходные значения уровней фактора и получены данные величины отклика.
Количество факторов: n1 1
Количество уровней фактора в опыте: |
N 7 |
|
i |
1 N |
|
||||||
Матрица плана эксперимента (в натуральных значениях): |
|
|
|||||||||
x1 12 |
x2 14 |
x3 16 |
x4 18 |
|
x5 20 |
x6 22 |
|||||
|
|
|
|
Xx x1 x2 x3 x4 x5 x6 x7 |
|
||||||
Количество повторностей опыта: |
|
k 3 |
|
jj 1 3 |
|
||||||
Результаты проведения опыта: |
|
|
|
|
|
|
|
||||
y1 1 |
|
91.2 |
y2 1 |
94.3 |
y3 1 |
96.4 |
|
y4 1 |
97.5 |
y5 1 |
|
y1 2 |
|
91.5 |
y2 2 |
94.0 |
y3 2 |
96.1 |
|
y4 2 |
97.4 |
y5 2 |
|
y1 3 |
|
91.8 |
y2 3 |
93.8 |
y3 3 |
95.8 |
|
y4 3 |
97.0 |
y5 3 |
|
y6 1 |
|
97.3 |
y6 2 |
97.0 |
y6 3 |
96.8 |
|
|
|
|
|
y7 1 |
|
95.5 |
y7 2 |
94.7 |
y7 3 |
94.5 |
|
|
|
|
|
|
|
|
|
|
|
|
yi jj |
|
|
||
Среднее значение результата: |
Ycpi |
jj |
|
|
|
|
|||||
k |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
x7 24
98.998.598.2
94
Дисперсия каждого опыта: |
|
|
|
1 |
|
|
|
2 |
|
S2i N 1 yi jj Ycpi |
|
||||||
|
|
|
||||||
Наибольшее значение дисперсии: |
|
|
|
|
jj |
|
|
|
S2max max(S2) |
|
|||||||
Количество степеней свободы: 1 |
S2max 0.093 |
|
|
|||||
k 1 |
|
1 |
2 |
|
||||
|
2 N 1 |
|
2 |
6 |
|
|||
Значение G-критерия Кохрена: |
G |
S2max |
|
G 0.359 |
|
|||
S2i |
|
|
||||||
|
|
|
||||||
|
|
|
i |
|
|
|
|
|
Табличное значение критерия Кохрена: |
Gтабл 0.9985 |
|
||||||
Ycpi |
S2i |
91.50.03
94.033 0.021
96.10.03
97.3 0.023
98.533 0.041
97.033 0.021
94.90.093
G Gтабл 1
Поскольку условие оказалось не ложным (равным 1, а не нулю), то гипотезу следует принять (не отвергнуть), то есть мы должны сделать вывод об однородности дисперсий и, следовательно, о достаточной достоверности (воспроизводимости) эксперимента.
Укажем координату дополнительной (нулевой точки): |
|
|
|
|
|
|
||||||
x0 x1 x2 x1 |
|
x0 10 |
|
|
|
|
|
|
||||
Дисперсия воспроизводимости эксперимента: |
|
|
|
|
|
|
|
|||||
|
|
S2i |
|
|
|
|
|
|
|
|
||
S2y |
|
i |
|
|
|
S2y 0.037 |
|
|
|
|
||
|
|
N |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
Поиск линейного уравнения регрессии (k=1) |
|
|
|
x1 |
Ycp1 |
|
||||||
Для получения исходной матрицы data используем значения |
|
|
|
|||||||||
векторов Xx и Ycp. |
|
|
|
|
|
|
|
|
|
x2 |
Ycp2 |
|
Выполняем математические преобразования для получения |
x |
Ycp |
|
|||||||||
коэффициентов уравнения регрессии в виде полинома: |
|
|
|
3 |
3 |
|
||||||
|
|
k 1 |
|
|
|
|
|
data x4 |
Ycp4 |
|
||
Выделяем столбцы факторов:0 |
|
|
1 |
|
|
|
|
|
Ycp5 |
|
||
|
|
|
|
|
|
x5 |
|
|||||
X data |
|
|
Y data |
n 7 |
|
|
|
x |
Ycp |
|
||
Количество строк матрицы: |
n rows (data) |
|
|
|
6 |
6 |
|
|||||
Поиск коэффициентов регрессии: C |
regress(X Y k) |
T |
|
x7 |
Ycp7 |
|||||||
coeffs submatrix(C 3 length(C) 1 0 0) |
|
(89.639 0.333 ) |
|
|||||||||
coeffs |
|
|||||||||||
Значения коэффициентов регрессии: |
|
b0 89.639 |
|
b1 0.333 |
|
|||||||
Уравнение регрессии: |
|
|
|
|
|
Y' ( x) |
b0 |
b1 x |
|
|
||
Расчетные значения по уравнению регрессии: |
Ypi b0 |
b1 xi |
|
|
|
|||||||
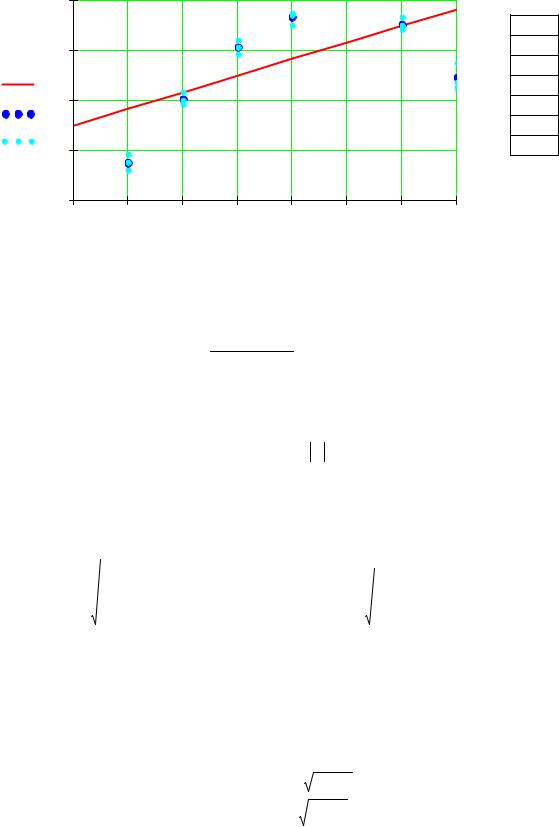
Строим график опытных данных. Выбираем двумерный график и для Yp задаем тип линии lines, а для Ycp – points (рис. 2.15).
|
Ypi |
|
Ycpi |
||
Средние значения результатов: Ypcp |
i |
|
Ycp |
i |
|
N |
N |
||||
|
|
||||
Ypcp 95.633 |
Ycp 95.629 |
||||
Остаточная сумма квадратов (финальный остаток):
95
|
|
|
k |
|
|
|
|
|
|
|
S2R Ypi Ycpi 2 |
|
|
S2R 4.558 |
|
||
|
|
|
i 1 |
|
|
|
|
|
|
98 |
|
|
|
|
|
|
Ypi |
|
|
|
|
|
|
|
|
93.635 |
|
96 |
|
|
|
|
|
|
94.301 |
Y'(x) |
|
|
|
|
|
|
94.967 |
|
|
|
|
|
|
|
|
||
Ycp |
|
|
|
|
|
|
|
95.633 |
94 |
|
|
|
|
|
|
96.299 |
|
y |
|
|
|
|
|
|
|
96.965 |
|
92 |
|
|
|
|
|
|
97.631 |
|
|
|
|
|
|
|
|
|
|
90 10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
|
|
|
|
x |
|
|
|
|
|
|
|
Рис. 2.15. Влияние величины Х на Y |
|
||||
Уровень критерия проверки гипотезы (значимости ошибки): 0.05 Дисперсия отклонения результатов расчета от опытов:
S2R
S2ад N (n1 1) S2ад 0.9116
F-критерий Фишера: S0 S2ад |
S1 S2y |
F max (S) |
F 24.544 |
|
|
min(S) |
|
Критическое значение F-критерия Фишера: |
Fkp qF 1 1 2 |
||
|
|
F Fkp 0 |
Fkp 5.143 |
Поскольку условие оказалось ложным (равным нулю, а не 1), то гипотезу следует отвергнуть (не принимать), то есть мы должны сделать вывод о неравноточности или неравнорассеянности дисперсий (значимы различия представленных выборок), следовательно, полученная модель неадекватно описывает результаты опытов.
Скорректированные средние квадратичные отклонения результатов:
|
|
1 |
|
N |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
1 |
Ycp Ycpi 2 |
|||||
Sx |
|
Ypcp Ypi 2 |
|
Sy |
|||||||||||
|
|
N 1 |
|
N 1 |
|||||||||||
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
i |
|
Sx 1.439 |
|
|
|
|
Sy 2.365 |
||||||||||
Выборочный корреляционный момент: |
|
|
|
|
|
|
|
|
|
||||||
Kxy |
1 |
Ycp Ycpi Ypcp Ypi |
Kxy 2.068 |
||||||||||||
N 1 |
|||||||||||||||
|
|
|
|
|
i |
|
|
|
Kxy |
|
|
|
|||
Коэффициент корреляции: |
r |
|
r 0.608 |
||||||||||||
Sy Sx |
|||||||||||||||
|
|
|
|
|
|
||||||||||
t-критерий коэффициента корреляции: tr |
|
r N 2 |
|
tr 1.712 |
|||||||||||
|
1 r2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
96

Табличное значение t-критерия: |
Tr |
|
|
1 |
|
|
k 1 1 |
|
qt |
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
tr |
Tr 1 |
|
Tr 12.706 |
||||
Поскольку условие оказалось не ложным (равным 1, а не 0), то мы должны сделать вывод о несущественности различий в представленных выборках, то есть вычисленное значение коэффициента корреляции недостоверно.
Поиск уравнения регрессии второго порядка (k=2)
Для получения исходной матрицы data используем значения векторов Xx и Ycp. k 2
Выполняем математические преобразования для получения коэффициентов уравнения
регрессии в виде полинома: |
|
|
|
x1 |
Ycp1 |
|
|
Выделяем столбцы факторов: |
|
|
|
||||
|
X data 0 |
Y data 1 |
|
|
|
|
|
Количество строк матрицы: n rows(data) |
n 7 |
x2 |
Ycp2 |
||||
x |
Ycp |
|
|||||
Поиск коэффициентов регрессии: |
C regress(X Y k) |
3 |
3 |
|
|||
coeffs |
submatrix(C 3 length(C) 1 0 0) |
data x4 |
Ycp4 |
|
|||
|
T |
4.736 |
0.122 ) |
|
|
|
|
coeffs (51.964 |
x5 |
Ycp5 |
|||||
Значения коэффициентов регрессии: |
|
|
|||||
|
|
x6 |
Ycp6 |
|
|||
b0 51.964 |
b1 4.736 |
b2 0.122 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x7 |
Ycp7 |
|
Уравнение регрессии: |
|
|
|
|
Y(x) b0 b1 x b2 (x)2 |
|||
Расчетные значения по уравнению регрессии: |
Ypi b0 |
b1 xi b2 xi 2 |
||||||
Строим график опытных данных. Выбираем двумерный график и для Yp задаем тип |
||||||||
линии lines, а для Ycp – points (рис. 2.16). |
|
|
|
|
||||
|
98 |
|
|
|
|
|
|
Ypi |
|
|
|
|
|
|
|
|
91.228 |
Y(x) |
96 |
|
|
|
|
|
|
94.356 |
|
|
|
|
|
|
|
96.508 |
|
Ycp |
94 |
|
|
|
|
|
|
97.684 |
|
|
|
|
|
|
97.884 |
||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
97.108 |
|
|
92 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
95.356 |
|
|
|
|
|
|
|
|
|
|
|
90 10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
|
|
|
|
x |
|
|
|
|
|
|
|
Рис. 2.16. Влияние величины Х на Y |
|
||||
|
|
Ypi |
|
Ycpi |
||
Средние значения результатов: |
Ypcp |
i |
|
Ycp |
i |
|
N |
N |
|||||
|
|
|
||||
|
Ypcp 95.732 |
Ycp 95.629 |
||||
97
Остаточная сумма квадратов (финальный остаток):
|
k |
|
|
|
|
|
|
S2R Ypi Ycpi 2 |
S2R 4.558 |
|
|||||
|
i 1 |
|
|
|
|
|
|
Дисперсия отклонения результатов расчета от опытных данных: |
|
||||||
S2ад |
S2R |
|
|
S2ад 0.0356 |
|
||
N (n1 1) |
|
||||||
F-критерий Фишера: S0 |
S2ад |
S1 |
S2y |
F max(S) |
F 1.043 |
||
|
|
|
|
|
|
min(S) |
|
Критическое значение F-критерия Фишера: |
Fkp qF 1 1 2 |
||||||
|
|
|
|
|
F |
Fkp 1 Fkp |
5.143 |
Поскольку условие оказалось не ложным (равным 1, а не нулю), то гипотезу следует |
|||||||
принять (не отвергнуть), то есть мы должны сделать вывод о равноточности или равнорассеянности дисперсий (различия представленных выборок незначимы), следовательно, полученная модель адекватно описывает результаты опытов.
Скорректированные средние квадратичные отклонения результатов:
|
|
|
1 |
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
2 |
||||||
Sx |
Ypcp |
Ypi |
|
Sy |
|
|
|
Ycp |
Ycpi |
|||||||||||
|
|
N 1 |
|
|
|
|
|
N 1 |
|
|||||||||||
Sx 2.354 |
i 1 |
|
|
|
|
Sy 2.365 |
i |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
Выборочный корреляционный момент: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Kxy 5.479 |
|
|
|||
Kxy N 1 Ycp Ycpi Ypcp Ypi |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
i |
|
|
|
|
|
Kxy |
|
|
|
|
|
|
|
|
|
Коэффициент корреляции: |
r |
|
|
|
|
|
r 0.9843 |
|
|
|||||||||||
|
Sy Sx |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
t-критерий коэффициента корреляции: |
tr |
|
r N 2 |
|
|
|
tr 12.453 |
|
||||||||||||
|
1 r2 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Табличное значение t-критерия: |
|
|
|
|
|
|
|
k 1 1 |
|
|
|
|||||||||
Tr qt 1 |
2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
tr |
Tr 0 |
|
|
|
Tr 4.303 |
|
|
||||
Поскольку условие оказалось ложным (равным нулю, а не 1), то мы должны сделать вывод о существенности различий в представленных выборках, то есть вычисленное значение коэффициента корреляции достоверно.
Оптимизация значений (поиск экстремума) функции
Начальное приближение: |
Xn x5 |
Xn 20 |
Ключевое слово начала вычислительного блока: |
Give |
|
Поиск максимума с помощью функции maximize (минимум – minimize): P MaximizeY( Xn)
Вычисленное значение x, соответствующее максимуму: P 19.41
Значение искомой функции, соответствующее экстремуму: Y(19.41) 97.926
98
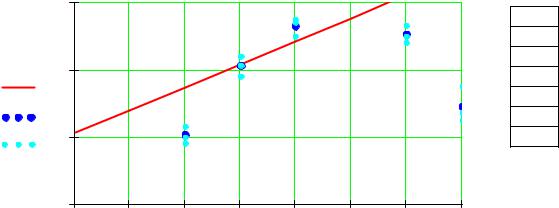
Преобразуем исходные данные в соответствии с используемой |
x1 |
s1 |
|
|||
функцией, сделав замену переменной: |
|
|
|
|
||
1 |
|
|
x2 |
s2 |
||
si |
|
|
|
x |
s |
|
Ycp |
|
|||||
|
i |
|
3 |
3 |
|
|
Для получения исходной матрицы data используем значения |
data x4 |
s4 |
||||
векторов S и Ycp. |
|
x |
s |
|
||
k 1 |
|
|||||
|
5 |
5 |
|
|||
Выполняем математические преобразования для получения |
x |
s |
|
|||
коэффициентов уравнения регрессии в виде полинома. |
6 |
6 |
|
|||
Выделяем столбцы факторов: X data 0 |
Y data 1 |
x7 |
s7 |
|||
Количество строк матрицы: |
n rows(data) |
|
|
|
|
n 7 |
|
|
|
||||||||
Поиск коэффициентов регрессии: |
C regress(X Y k) |
|
|
|
|
|
|
|
|
||||||||
coeffs submatrix(C 3 length(C) |
1 0 0) |
coeffsT 0.011 3.731 10 5 |
|||||||||||||||
Значения коэффициентов регрессии: |
|
|
b0 0.011 |
|
|
b1 3.731 10 5 |
|||||||||||
Уравнение регрессии после преобразования: |
Y'(x) |
|
b |
0 |
b |
1 |
x |
|
1 |
||||||||
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||
Расчетные значения по уравнению регрессии: Ypi |
|
|
|
|
|
|
|
|
|
|
|
||||||
b0 b1 xi |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
Ycpi |
|
|
|
|
|
|
|
Ypi |
||||||
Средние значения результатов: |
Ycp |
|
i |
|
|
|
|
Ypcp |
|
|
i |
|
|
|
|||
|
N |
|
|
|
|
|
|
|
N |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Ycp 95.629 |
|
|
Ypcp 95.732 |
|||||||||||||
Остаточная сумма квадратов (финальный остаток): |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S2R Ypi Ycpi 2 |
|
|
|
|
|
|
S2R 10.668 |
||||||||||
i 1
Строим график опытных данных. Выбираем двумерный график и для Yp задаем тип линии lines, а для Ycp – points (рис. 2.17).
|
98 |
|
|
|
|
|
|
Ypi |
|
|
|
|
|
|
|
94.766 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
95.441 |
Y'(x) 96 |
|
|
|
|
|
|
96.126 |
|
|
|
|
|
|
|
96.82 |
||
Ycp |
|
|
|
|
|
|
|
97.525 |
|
|
|
|
|
|
|
98.24 |
|
y |
|
|
|
|
|
|
|
|
94 |
|
|
|
|
|
|
98.965 |
|
|
|
|
|
|
|
|
||
|
92 10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
x
Рис. 2.17. Влияние величины Х на Y
99

Уровень критерия проверки гипотезы (значимости ошибки): |
0.05 |
|||
Дисперсия отклонения результатов расчета от опытов: |
|
|||
S2ад |
S2R |
|
S2ад 0.0356 |
|
N (n1 1) |
|
|||
F-критерий Фишера: S0 S2ад |
S1 S2y |
F max(S) |
F 57.445 |
|
|
|
|
min(S) |
|
Критическое значение F-критерия Фишера: Fkp qF 1 1 2 |
||||
|
|
F |
Fkp 0 |
Fkp 5.143 |
Поскольку условие оказалось ложным (равным нулю, а не 1), то гипотезу следует отвергнуть (не принимать), то есть мы должны сделать вывод о неравноточности или неравнорассеянности дисперсий (различия представленных выборок значимы), следовательно, полученная модель неадекватно описывает результаты опытов.
Скорректированные средние квадратичные отклонения результатов:
|
|
1 |
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||
Sx |
|
Ypcp Ypi 2 |
|
|
|
Sy |
|
Ycp Ycpi 2 |
|||||||||
|
|
N |
1 |
|
|
|
|
N 1 |
|||||||||
Sx 1.512 |
|
i 1 |
|
|
|
Sy 2.365 |
|
i |
|||||||||
|
|
|
|
|
|
|
|||||||||||
Выборочный корреляционный момент: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Kxy |
1 |
Ycp Ycpi Ypcp Ypi |
|
|
Kxy 2.138 |
||||||||||||
N 1 |
|
|
|||||||||||||||
|
|
|
|
|
i |
|
|
|
Kxy |
|
|
|
|
|
|
|
|
Коэффициент корреляции: |
r |
|
|
|
|
|
|
|
r 0.5982 |
||||||||
|
Sy Sx |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
t-критерий коэффициента корреляции: |
tr |
|
|
r N 2 |
|
|
|
|
tr 1.669 |
||||||||
|
|
1 r2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Табличное значение t-критерия: |
|
|
|
|
1 |
|
k |
|
|
||||||||
Tr qt |
2 |
1 1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
tr |
Tr |
1 |
|
|
|
|
|
Tr 12.706 |
|||
Поскольку условие оказалось не ложным (равным 1, а не 0), то различия представленных выборок не существенны, а коэффициент корреляции не достоверен.
Проведение факторного эксперимента осуществляется по заранее намеченной стратегии исследования для изучения влияния одновременно нескольких факторов. При обработке данных вид формальной математической модели задается до проведения эксперимента, а в ходе его определяются только значения коэффициентов.
Проведение экспериментов, как правило, производится только на двух уровнях факторов: нижнем (–1) и верхнем (+1) или сокращенно «–, +» уровнях, что сокращает объем экспериментальной работы. В ряде способов
100
