Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пензенский Государственный Университет Архитектуры и Строительства

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2286

.pdf

Скачиваний:

Добавлен:

16.06.2024

Размер:

6.42 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 118 9 10 11 > Следующая >>>

Уравнение метода сил примет вид:

11 Х1 1 1 .

Здесь:

1EI 1 dx

1 l 3

;

3EI

1 1 l ; 1 0.

Тогда:

Х1 1 l 0

1 3EI

3EI .

3EI

l l

Окончательная эпюра моментов (рис. 7.2, г) получается путем исправления единичной эпюры: Mок M1 X1 .

Аналогично строятся эпюры моментов и определяются концевые реакции и для других случаев загружения или перемещения одного из узлов балки. Найденные решения приведены в таблице метода перемещений (табл. 7.1).

	Таблица метода перемещений	Таблица 7.1
	Таблица метода перемещений

№	Схемы балок и эпюры изгибающих моментов	Формулы моментов
п/п	Схемы балок и эпюры изгибающих моментов	и реакций

1	2			3

1				i	EI
				i
					l	3i
			M A			3i
						l
		V	A	V		3i
			A		B		l2
							l2
2			M A 3i
		V	A	V		3i
			A		B		l
							l

Продолжение табл.

7.1

M A ql

5 ql

3 ql

M A

Fl v(1 v2 )

VA Fv

(3 v2 )

(3 u)

M A

m(l

)

2l2

3m(l2 b2 )

2l3

M A

Pab

M B

Pa2b

Pb2

Pa2

Окончание табл. 7.1

1	2				3

7		M A		mb		2l 3b
					l2
		M B		ma 2l 3a
					l2		6ab
		R	A	R			6ab	m
		R		R				m
					B		l3
							l3

8		M A			M B 6i
							l
		V		A	V	12i
				A	B		l2
							l2

M A 4i

M B 2i

VA VB 6li

10	M A M B				ql	2
	M A M B				ql
					12
	V	A	V	ql
		A	B		2
					2

7.2.Расчет кинематически неопределимой системы

содним неизвестным методом перемещений

Пример №1.

Построить эпюры внутренних усилий для рамы с помощью метода перемещений (рис. 7.3, а).

Найдем соотношение погонных жесткостей для стержней рамы:

i	EI	i ;
i		i ;
1	6
	6
i 2EI			EI	EI EI 6 6 EI 3i .
2	4		2	2 6 EI 2 6
	4		2	2 6 EI 2 6

1) Количество неизвестных:

n nу nл .

где nу – количество угловых перемещений, равно количеству жестких узлов: nу=1;

nл – количество линейных перемещений, равно количеству степеней свободы шарнирной схемы.

Шарнирная схема получается из заданной системы путем введения шарниров во все узлы, включая опорные:

nл Wш.с. 3Д 2Ш СО 3 2 2 1 4 0 .

nnу nл 1 0 1.

2)Основная система метода перемещений (О.С.М.П.) получается из заданной системы путем введения дополнительных связей (рис. 7.3, б).

Рис. 7.3. Расчетная схема и основная система метода перемещений

3) Уравнение метода перемещений с одним неизвестным имеет вид:

r11 Z1 R1р 0 .

4) Единичная эпюра строится в основной системе с использованием таблицы метода перемещений (табл. 7.1) от единичного перемещения

Z1 1 (рис. 7.4, а,б).

Рис. 7.4. Единичная и грузовая эпюры

5) Вычисление коэффициента при неизвестном выполняется статическим способом (для реакций в дополнительно введенных защемлениях используется метод вырезания узлов):

M узл 0 : 9i 4i r11 0 ; r11 9i 4i 13i .

6)Грузовая эпюра (рис. 7.4, в) строится в основной системе с помощью таблицы метода перемещений от действия внешней нагрузки.

7)Вычисление свободного члена уравнения статическим способом:

M узл 0 : 52 R1p 0 ;

R1 p 52 .

8) Решение уравнения метода перемещений: 13i Z1 52 0 ;

Z1 1352i 4i .

9) Исправленная эпюра M1и M1 Z1 (рис. 7.5, а).

10) Окончательная эпюра моментов (рис. 7.5, б) строится в заданной системе и получается путем сложения грузовой и исправленной эпюр:

Mок M p M1и .

Рис. 7.5. Исправленная и окончательная эпюры

Статическая проверка окончательной эпюры моментов заключается в равновесии вырезанного жесткого узла (рис. 7.5, в):

M узл 0 :

16 16 0;

0 0, верно.

11) Эпюры поперечных (рис. 7.6, а) и продольных (рис. 7.6, б) сил, статическая проверка (рис. 7.6, в).

Рис. 7.6. Эпюры поперечных и продольных сил, статическая проверка

Fkx 0 : 4 4 0 ; 0=0, верно.

Fky 0 : 56 26 4 48 0 ; 0=0, верно.

M A 0 : 26 4 2 4 6 48 4 8 0; 0=0, верно.

Mmax 48 1,846 26 1,846 1,8462 44,308.

7.3.Расчет кинематически неопределимой системы

сдвумя неизвестными методом перемещений

Пример №1.

Построить эпюры внутренних усилий для рамы с помощью метода перемещений (рис. 7.7, а).

Рис. 7.7. Расчетная схема и основная система метода перемещений

Найдем соотношение погонных жесткостей для стержней рамы: i1 3EI6 3i ;

i2 2EI6 2i ; i3 E6I i .

1) Количество неизвестных:

n nу nл .

nу=1 (количество жестких узлов);

nл Wш.с. 3Д 2Ш СО 3 3 2 2 4 1. n nу nл 1 1 2 .

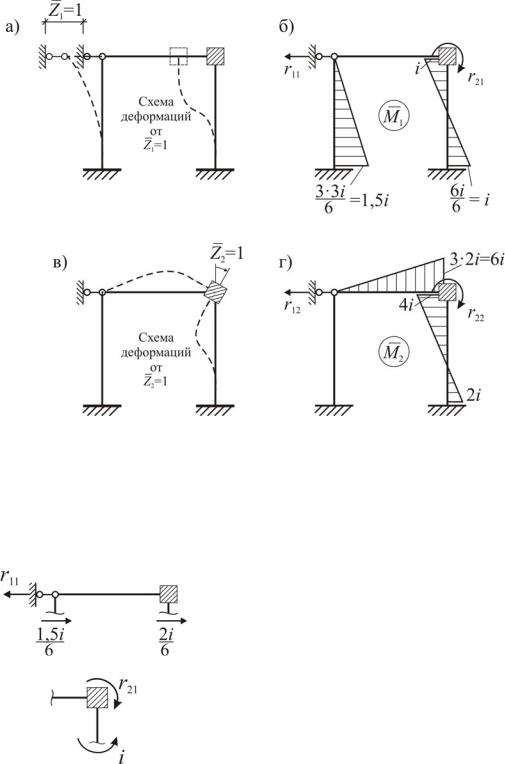
2)Основная система метода перемещений (О.С.М.П.) показана на рис. 7.7, б.

3)Система уравнений метода перемещений с двумя неизвестными:

r11 Z1 r12 Z2 R1 р 0

r21 Z1 r22 Z2 R2 р 0

4) Единичные эпюры (рис. 7.8).

Рис. 7.8. Единичные эпюры

5) Вычисление коэффициентов при неизвестных выполняется статическим способом (для реакций в дополнительно введенных защемлениях используется метод вырезания узлов; для реакций в дополнительно введенных линейных связях проводится сечение, параллельное реакции, так, чтобы в отсеченной части была только одна неизвестная сила):

x 0 : 1,56 i 26i r11 0 ; r11 1,56 i 26i 3,56 i .

M узл 0 : i r21 0 ; r21 i .

x 0 : i r12 0 ; r12 i .

M узл 0 : 6i 4i r22 0 ; r22 6i 4i 10i .

6) Грузовая эпюра (рис. 7.9, а) строится только от пролетной внешней нагрузки.

Рис. 7.9. Грузовая эпюра и вычисление свободных коэффициентов

7)Вычисление свободных коэффициентов уравнений статическим способом (рис. 7.9, б):

x 0 : 9 R1 p 10 0 ; R1 p 9 10 1.

M узл 0 : 27 R2 p 0 ; R2 p 27 .

8)Решение системы уравнений метода перемещений:

3,5i	Z1 i Z2 1 0					10				35i Z1			10i Z2						10 0
6	Z1 i Z2 1 0									6
6										6
i Z	10i Z	2		27	0						6i Z		10i Z				2		27 0
1		2				( 1)					6	1					2
29i Z 37 0; Z 37 6 7,6552 .											6
29i Z 37 0; Z 37 6 7,6552 .
6	1				1	29i	i
6						29i	i
	27 i Z				27 i 7,6552					3,4655
Z2			1			i						.
Z2	10i		1			10i					i	.
	10i					10i					i
9) Исправленные эпюры M и									Z ,		M и M				Z			(рис. 7.10, а, б).
9) Исправленные эпюры M и							M	1	Z ,		M и M			2	Z	2		(рис. 7.10, а, б).
						1		1		1	2			2		2
							79

10) Окончательная эпюра моментов (рис. 7.10, в) получается путем сложения грузовой и исправленных эпюр: Mок M p M1и M2и .

Рис. 7.10. Исправленные и окончательная эпюры

Статическая проверка окончательной эпюры моментов заключается в равновесии вырезанного жесткого узла:

M узл 0 : 6,207 6,207 0 ; 0 0, верно.

11) Эпюры поперечных (рис. 7.11, а) и продольных (рис. 7.11, б) сил, статическая проверка (рис. 7.11, в).

Рис. 7.11. Эпюры поперечных и продольных сил, статическая проверка

Fkx 0 : 13,086 0,914 4 6 10 0 ; 0=0, верно.

Fky 0 : 10,966 13,034 24 0 ; 0=0, верно.

M A 0 : 6,517 4 6 3 24 3 10 6 0,724 13,034 6 0 ;0,003 0 , верно.

<<< < Предыдущая 1 2 3 4 5 6 78 / 118 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.06.20246.35 Mб02281.pdf
#
16.06.20246.37 Mб02282.pdf
#
16.06.20246.39 Mб02283.pdf
#
16.06.20246.4 Mб02284.pdf
#
16.06.20246.41 Mб02285.pdf
#
16.06.20246.42 Mб02286.pdf
#
16.06.20246.42 Mб02287.pdf
#
16.06.20246.45 Mб02288.pdf
#
16.06.20246.45 Mб02289.pdf
#
17.06.2024241.76 Кб0229.pdf
#
17.06.20246.45 Mб02290.pdf