
2254
.pdf
Рассматривая узел B, найдем |
|
|
|
|
|
|
|
|
|
|
Y 0; SAB(P ) SBC(P ) cos45 SBD(P ) cos45 0 . |
|
|
|
|||||||
|
|
|
2 |
|
|
2 |
|
|
P |
|
Откуда SAB(P ) SBD(P ) SBC(P ) cos45 P |
2 |
|
|
P 2 |
|
|
|
|
|
. |
3 |
2 |
|
3 |
|||||||
|
|
|
|
|
|
|
|
|||
Поскольку окончательное усилие в стержне ВС должно равняться нулю, запишем условие:
SBC SBC(1) X1 SBC(P ) 0.
Решая это уравнение относительно Х1, получим:
|
S P |
2P |
2 3 |
|
|
X |
BC |
|
|
|
2P. |
|
|
|
|||
1 |
SBC(1) |
3 |
2 |
|
|
|
|
||||
Находим усилие в стержне АВ:
SAB SAB(1) X1 SAB(P ) 13 ( 2P) P3 P.
Пр и м е р 2 . 3 . Определить усилие в стержне АВ фермы, изобра$ женной на рис. 2.7.
Рис.2.7
Эта задача решается аналогично предыдущей.
Здесь следует убрать опорный стержень в точке А и ввести новый стержень ВЕ.
О т в е т : усилие S |
|
|
P |
2 . |
|
AB |
|
||||
|
|
2 |
|
||
П р и м е р |
2 . 4 . |
|
|
||
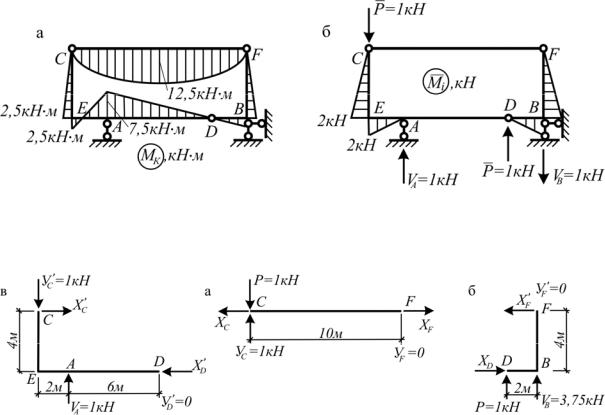
Построить эпюры внутренних усилий в раме |
|||||
(рис.2.8,а). |
|
|
|
|
|
Разложим |
нагрузку на |
симметричную и кососимметричную |
|||
(рис.2.8,б,в). |
|
|
|
|
|
21

Рис.2.8
Найдем реакции опор и силы взаимодействия шарниров только от нагрузки, показанной на рис.2.9,в. Расчленим раму 1 на звенья 2, 3, 4 (рис.2.9, г, д, е).
Рис.2.9
22

Из равновесия рамы I:
I. 1) MF 0; 60 2 6 40 2 40 6 Y G 8 0;
720 80 240 YG 8;YG 110 кН.
2) MG 0; YF 8 60 6 2 40 6 40 2 0; YF 100 кН.
II.1) MD 0; XAB 0;
2)MA 0; XD 60;
3)Y 0;YD 110;
III. 1) ME 0; XCB 120;
2)Mc 0; XE 180;
3)Y 0;YE 110.
Сучетом сил на рис. 2.9,г,д,е, строим эпюры на рис.2.9,а,б. Эпюру Mок (рис.2.10) построим как Mок Mc Mkc .
Рис.2.10
П р и м е р 2 . 5 . По консольному балочному однопролетному мосJ ту l = 24 м, а=2 м равномерно перемещаются 2 груза Р1=3 кН, Р2=4 кН со скоростью соответственно v1=2 м/с и v1=3 м/с. Второй груз въехал на мост через t=8 с после первого. Пренебрегая массой моста и грузов, определить максимальное давление моста на опору В.
При решении задачи воспользуемся теоремой о критическом положении системы подвижных грузов над полигональной линией влияния, в соответствии с которой одна из сил должна располагаться над одной из вершин линии влияния.
Построим линию влияния реакции VB (рис. 2.11) и расположим силу Р1 в точке D над максимальной ординатой этой линии влияния.
23

Рис.2.11
В начале движения расстояние между грузами было равно: а1 v1t 2 8 16 м.
Определим время, за которое первый груз переместился до точки D, начиная с того момента времени, когда второй груз въехал на балку:
S l 2a a1 28 16 12 м ;
t1 S 12 6 с . v1 2
Найдем расстояние а2 между грузами в критическом положении. За время t1 второй груз приблизился к первому на расстояние:
S v2 v1 t1 3 2 6 6 м .
Тогда a2 a1 S 16 6 10 м.
Таким образом, критическое положение системы грузов установлеJ но, причем соответствующие ему ординаты линий влияния Vв под грузами составят:
у |
|
х1 |
|
26 |
|
13 |
; |
y |
|
x2 |
|
l a a2 |
|
24 2 10 |
|
2 |
. |
|
|
|
|
|
|
|
|||||||||||
1 |
l |
24 12 |
|
2 |
l |
|
l |
24 |
3 |
|
|||||||
|
|
|
|
|
|
|
|||||||||||
Определяем реакцию VB в этом положении, равную по модулю передаваемому давлению на опору:
VB P1y1 P2 y2 3 1312 4 32 5,92 кН.
24

П р и м е р 2 . 6 . С помощью балочного передающего устройства, показанного на рис. 2.12, добиться уменьшения на опоре В изгибающего момента на 25 %. Выбрать длину передающего устройства 2х.
Задача решается путем построений линий влияния изгибающего момента в сечении В (МB) с учетом узловой передачи нагрузки в точках
D и Е.
Найдем величину МB по линии влияния без учета передающего устройства:
МB q 2l 32 l 12 38 ql 2 .
Рис.2.12
Ординаты уD, уЕ и уК (рис. 2.9) соответственно равны: |
|
|
|
|||||||||||||
y |
D |
|
l |
x ; y |
E |
|
l x |
; y |
K |
|
yD yE |
|
l / 2 x (l x) / 2 |
|
2l 3x |
. |
|
|
|
|
|
||||||||||||
|
2 |
|
2 |
|
2 |
2 |
4 |
|
||||||||
|
|
|
|
|
|
|
||||||||||
При узловой передаче нагрузки площадь линии влияния уменьJ шается на (площадь заштрихованного треугольника на рис. 2.9), величина которой составит:
|
1 |
l |
|
2l 3x |
|
3x2 |
|||
|
|
2x |
|
|
|
|
|
|
. |
2 |
2 |
|
4 |
||||||
|
|
|
4 |
|
|
||||
Площадь усеченной линии влияния будет
38 l 2 34 x2 38 l 2 2x2 .
При введении передающего устройства изгибающий момент МВ в точJ ке В должен составить 75 % от момента без учета этого устройства, т.е.
34 38 ql 2 38 q l 2 2x2 , или 0,75l 2 l 2 2x2 ; x2 0,125l 2 .
25

Решая это уравнение относительно х, найдем, что х=0,353l. Соответственно длина передающего устройства будет при этом
|
2x 0,706l . |
|
|
|
|
|
|
|
|
|
|
|
|
||
П р и м е р 2 . 7 . |
Построить линии влияния усилий в указанных |
||||||||||||||
стержнях фермы (рис. 2.13). |
|
|
|
|
|
|
|
|
|
|
|
|
|||
При решении задачи важно установить последовательность поJ |
|||||||||||||||
строения линий влияния. Сначала необходимо построить линию влияJ |
|||||||||||||||
|
ния усилия S2. Для этого проведем сечеJ |
||||||||||||||
|
ние IJI (см. рис. 2.13) и рассмотрим равJ |
||||||||||||||
|
новесие правой части фермы (рис. 2.14,а), |
||||||||||||||
|
считая, что груз Р=1 находится слева от |
||||||||||||||
|
указанной панели. Составим уравнение |
||||||||||||||
|
равновесия (узел D не загружен): |
|
|
||||||||||||
|
У 0; |
S2 sin 0; |
sin 0; S2 |
0. |
|||||||||||
|
При положении груза Р=1 в узле D |
||||||||||||||
|
рассмотрим равновесие той же части |
||||||||||||||
|
фермы. Тогда |
|
|
|
|
|
|
|
|
|
|
||||
|
У 0; |
|
Р S2 sin 0; |
|
S2 |
|
1 |
; |
|||||||
|
|
sin |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
sin |
AC |
|
|
4 |
|
1 |
; |
S |
|
1,8. |
|
|
||
|
|
|
|
1,8 |
2 |
|
|
||||||||
Рис.2.13 |
|
AB |
|
|
62 42 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
Рис. 2.14
Рис. 2.14,а,б,в соответствуют загруженным состояниям рассматриJ ваемых частей фермы. Чтобы построить линию влияния S3, вырежем узел А (см. рис. 2.14,б) и рассмотрим два положения груза Р=1.
26

При положении груза Р=1 за пределами панелей, смежных с узлом А, имеем:
У 0; |
S2 sin S3 0; |
S3 S2 sin ; |
S3 |
|
S2 |
. |
|
1,8 |
|||||||
|
|
|
|
|
|||
В случае, когда Р=1 находится в узле А, имеем:
У 0; |
S2 sin S3 P 0; |
S3 S2 sin 1; |
S3 |
|
S2 |
1 1. |
|
1,8 |
|||||||
|
|
|
|
|
|||
При построении линии влияния S1 проводим замкнутое сечение П (см. рис. 2.13) и вновь рассматриваем два положения единичного груза Р=1 (рис. 2.14,в). Когда Р=1 находится вне разрезанных панелей (слева или справа от узла Е):
У 0; |
S1 sin 0, |
sin 0, |
S1 0. |
При положении груза справа в узле Е:
У 0; |
Р S1 sin 0; |
S1 |
Р |
|
1,8 . |
||
sin |
|||||||
|
|
|
|
|
|||
Линии влияния усилий S1, S2 и S3 показаны на рис. 2.13. |
|||||||
П р и м е р |
2 . 8 . Построить линии |
|
|
|
|
||
влияния усилий в указанных стержнях |
|
|
|
|
|||
фермы (рис. 2.15). |
|
|
|
|
|
||
При решении задачи построение |
|
|
|
|
|||
линий влияния следует начинать с усиJ |
|
|
|
|
|||
лия S1, используя замкнутое сечение I, |
|
|
|
|
|||
а затем, проведя сечение IIJII, поJ |
|
|
|
|
|||
строить линии влияния усилий S2 и S3. |
|
|
Рис. 2.15 |
||||
П р и м е р |
2 . 9 . |
Найти взаимное |
сближение |
|
точек С и D по |
||
вертикали для системы, показанной на рис. 2.16. Считать сечение всех стержней одинаковым, т.е. EJ=const.
Взаимное сближение по вертикали точек С и D определяется по формуле Мора:
|
|
|
|
|
ik |
1 |
|
|
|
|
|
|
|
|
|
|
M |
i Mkdx , |
|
|
|||
|
|
|
|
|
EJ |
|
|
||||
|
|
|
|
|
|
|
(l ) |
|
|
||
где Мk – |
эпюра |
изгибающих |
моментов |
от заданной |
нагрузки |
||||||
|
|
|
|
(рис. 2.18,а); |
|
|
|
|
|
|
|
|
|
|
– |
эпюра |
изгибающих |
моментов в |
единичном |
состоянии |
|||
M |
i |
||||||||||
(рис. 2.18,б).
27

Рис.2.16
Для построения эпюры Мk в грузовом состоянии определим опорные реакции в точках А и В:
1. |
m(B) 0; |
VA 8 1 10 5 0; |
VA |
|
50 |
6,25кН. |
||||
8 |
||||||||||
|
|
|
|
|
|
|
32 2 |
|
||
2. |
m(A) 0; |
VB 8 1 2 1 1 8 4 0; |
|
|
VB |
|
3,75 . |
|||
|
|
8 |
||||||||
|
X 0; |
HB 0 . |
|
|
|
|
|
|
||
3. |
|
|
|
|
|
|
|
|||
Найдем также реакции в шарнирах С, D и F. Для этого расчленим систему на отдельные части (см. рис. 2.14а, б, в).
Рис.2.17
Из условия симметрии СF
|
|
Y Y |
9 10 |
5кН; |
||||||
|
|
|
||||||||
|
|
|
C |
F |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
X 0; |
XF XC 0; |
XC XF . |
||||||
Составим уравнения |
равновесия |
для |
правой части рамы DBF |
|||||||
(рис. 2.17,б): |
|
|
|
|
|
|
|
|
|
|
1. |
Y 0; |
YD VB YF |
0; |
|
|
YD 5 3,75 1,25кН; |
||||
2. |
m(B) 0; |
XF 4 YD 2 0; |
XF |
|
1,25 2 |
0,625 кН; |
||||
|
||||||||||
|
X 0; |
|
|
|
|
|
|
4 |
|
|
3. |
XD XF |
0; |
|
XD XF 0,625 кН. |
||||||
|
|
|
|
|
28 |
|
|
|
|
|
Рассматривая равновесие левой части рамы СЕАD (рис. 2.17,в), найдем
|
1. |
X 0; |
XС XВ 0; |
XС |
XВ |
0,625 ; |
||||||||
|
2. |
Y 0; |
VФ YС YD |
0; |
YD VA YC 6,25 5 1,25 кН. |
|||||||||
|
Вычислим изгибающие моменты в точках Е, В и К: |
|||||||||||||
|
|
|
q 102 |
|
|
|
|
|
|
|
|
|
||
M |
G |
|
|
12,5 кН·м; M |
EC |
M |
EA |
M |
BF |
M |
BD |
0,625 4 2,5 кН·м; |
||
8 |
||||||||||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
MAE 1,25 6 7,5 кН·м.
Эпюры изгибающих моментов Мk показаны на рис. 2.18,а.
Для построения эпюры изгибающих моментов в единичном состояJ нии определяем опорные реакции из условия равновесия рамы в целом.
1. m(А) 0; |
VB 10 1 8 1 2 0; |
VB 1; |
|
2. Y 0; |
VA VB 1 1 0; |
VA VB 1. |
|
Реакции в шарнирах С, F и D, как и в грузовом состоянии, определяютJ ся из условия равновесия отдельных частей рамы (см. рис. 2.19, а, б, в).
Рис.2.18
Рис.2.19
29

Из равновесия правой части DBF найдем:
m(B) 0; |
XF 4 1 2 0; |
XF |
0,5; |
XF XC XD XF |
0,5; |
||
X |
X |
X |
0,5. |
|
|
|
|
C |
D |
C |
|
|
|
|
|
Эпюра Mi показана на рис. 2.18,б.
Находим искомое перемещение по формуле Мора, вычисляя инJ теграл Мора по правилу Верещагина:
|
|
1 |
|
|
|
|
1 |
|
|
2,5 |
4 |
|
2 |
|
|
2,5 |
2 |
|
2 |
|
|
2 2 |
|
2 |
|
|
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
ik |
|
|
MiMkdx |
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2,5 |
|
|
7,5 |
|
|
|||
EJ (l ) |
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
3 |
||||||||||||||||||||
|
|
|
|
|
EJ |
|
2 3 |
|
|
|
2 3 |
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||
EJ1 403 13 53 15 кНEJ м3 .
Пр и м е р 2 . 1 0 . На каком расстоянии должны быть установлены шарнирные скобы А и В монтажной траверсы (рис.2.20), чтобы при подъеме грузов Р прогибы концов траверсы были равны половине выгиба
еесередины? Собственным весом траверсы пренебречь.
а) |
в) |
М2
б)
М1
Рис.2.20
Решение. На рис. 2.20,б,в, представлены единичные состояния и даны соответствующие эпюры изгибающих моментов Мi для определеJ ния, соответственно, удвоенного прогиба на концах консоли и прогиба в середине пролета. Ординаты грузовой эпюры Мр в Р раз больше
ординат эпюры М1 . Используя при вычислении перемещений правило
30
