2222

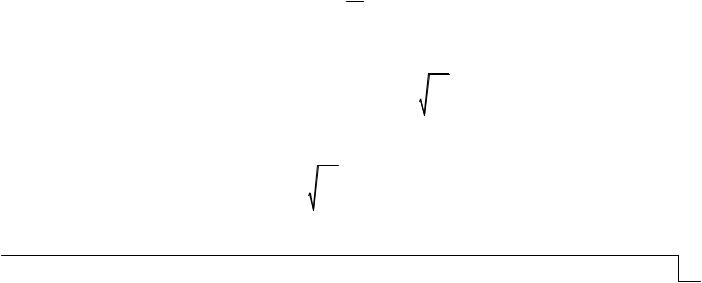
BUILDING STRUCTURES, BUILDINGS AND CONSTRUCTIONS

4AТр 4 17,94 71,8 см2 .

Момент инерции четырёх выкружек

Главные моменты инерции и сопротивления сечения нового профиля по сравнению с аналогом увеличились на 20 % каждый.

Момент инерции нового двутаврового профиля

JY 64 D4 d 4 12tсв bmax3 D3 .

В соответствии с действующими нормами назначается гибкость стенки, при которой не требуется проверка её устойчивости [5].

Ry= 230 МПа; Е=206000 МПа.

СТРОИТЕЛЬНЫЕ КОНСТРУКЦИИ, ЗДАНИЯ И СООРУЖЕНИЯ

Площадь сечения оставляется без изменений, она распределяется по сечению следующим образом. Высота сечения балки – 101,4 см. Высота стенки – 94,8 см. Момент сопротивления нового двутавра– 14827 см3.

Эффективностьнового балочного профиля 13,5 % (высокая).

Таким образом, новый прокатный профиль снижает материалоёмкость на 13,5 % по сравнению со стандартным профилем [4].

Особенно эффективен новый профиль для подкрановых балок, использующихся на предприятиях с тяжёлым режимом эксплуатации мостового крана [5], так как возникновение усталостной трещины в зоне выкружки невозможно, ввиду того что эффективный коэффициент концентрации напряжений близок к единице (Кэф ≈ 1), а толщина в зоне выкружки увеличена в 3,5 раза. Такой же эффективностью обладают и тавровые профили, полученные из предлагаемого двутаврового профиля.

Список литературы

1.Нежданов, К.К. Испытание неразрезных подкрановых балок на выносливость / К.К. Нежданов, И.Н. Гарькин // Региональная архитектура и строительство. – 2016.–

№2. – С.81–86.

2.Нежданов, К.К. Способ проката двутаврового профиля сечения из низколегированной стали / К.К. Нежданов, И.Н. Гарькин // Строительная механика и расчёт сооружений. – 2011. – №4. – С.51–55.

3.Нежданов, К.К. Эффективный способ проката уголкового профиля / К.К. Нежданов, Л.А. Железняков, И.Н. Гарькин // Строительная механика и расчёт сооружений. – 2014. – №1. – С.71–75.

4.СНиП II-23-81*. Стальные конструкции. Актуализированная редакция, Утверждён Министерством регионального развития Российской Федерации, 27.12.2010.

5.Управление безопасностью объектов повышенного риска / А.М. Данилов, О.А. Голованов, И.А. Гарькина, Э.В. Лапшин // Труды международного симпозиума

«Надёжность и качество».– 2007. – Т2.– С.109–112.

References

1.Nezhdanov, K.K. Testing of continuous crane beams for endurance / K.K. Nezhdanov, I.N. Garkin // Regional architecture and engineering. – 2016. – №.2. – P.81–86.

2.Nezhdanov, K.K. Method of rolling an I-section profile of low-alloyed steel / K.K. Nezhdanov, I.N. Garkin // Construction mechanics and calculation of structures. – 2011. – N4. – P.51–55.

3.Nezhdanov, K.K. Effective method of angle profile rolling / K.K. Nezhdanov, L.A. Zheleznyakov, I.N. Garkin // Construction mechanics and calculation of structures. – 2014. – No. 1. – P.71–75.

4.SNiP II-23-81 * Steel structures. Updated version, Approved by the Ministry of Regional Development of the Russian Federation, 27.12.2010.

5.Management of the safety of high-risk facilities / A.M. Danilov, O.A. Golovanov, I.A. Garkina, E.V. Lapshin // Proceedings of the International Symposium «Reliability and Quality». – 2007. – Vol.2. – P.109–112.

BUILDING STRUCTURES, BUILDINGS AND CONSTRUCTIONS

УДК 69.009 +37.07+331.108.4

УСЛОВИЯ ДЛЯ ИСПОЛЬЗОВАНИЯ КОЗЛОВОГО КРАНА ПРИ СЕЙСМИЧЕСКИХ ВОЗДЕЙСТВИЯХ

М.В. Арискин, И.Н. Гарькин

Дается обоснование возможности использования козлового крана при повышенных сейсмических воздействиях. Предлагается методика оценки с использованием проектновычислительного комплекса SCAD 11.5.

Ключевые слова: металлические конструкции, козловой кран, сейсмические воздействия, метод конечных элементов, вычислительный комплекс SCAD

CONDITIONS FOR THE USE OF A GANTRY CRANE UNDER

SEISMIC ACTION

M.V. Ariskin, I.N. Garkin

Feasibility of using a gantry crane under increased seismic action is given. The estimation technique is proposed using the SCAD 11.5 design-computing complex.

Keywords: metal structures, gantry crane, seismic actions, finite element method, computer complex SCAD

Козловой кран является одним из часто используемых в строительстве грузоподъёмных механизмов (ГПМ). Эффективность его применения определяется грузоподъемностью, высотой подъема груза, длиной пролета, районом строительства, а также особыми условиями эксплуатации. Ограничимся лишь сейсмическими воздействиями. Рассмотрим возможности использования крана при сейсмических воздействиях на основе специальных расчётов.

Приведём пример расчёта использования козлового крана К-651 в г.Керчи (условия эксплуатации на рис.1).

Расчет выполнен с помощью проектно-вычислительного комплекса SCAD [1]. Комплекс реализует конечно-элементное моделирование статических и динамических расчетных схем, проверку устойчивости, выбор невыгодных сочетаний усилий, проверку несущей способности стальных конструкций крана.

При моделировании [2, 3] крана (рис. 2, 3) использовались данные технического паспорта. С учётом неполной информации о работе элементов конструкции крана при моделировании принимались следующие допущения:

колесная база смоделирована по конфигурации крана объемными пространственными элементами без отверстий и с общей паспортной массой;

СТРОИТЕЛЬНЫЕ КОНСТРУКЦИИ, ЗДАНИЯ И СООРУЖЕНИЯ

аналогично колесной базе моделировался поворотный механизм и противовес;

сечения портала, башни, секций стрелы принимались по паспорту;

нагрузки колесной базы в общей работе крана не участвуют.

Рис.1. Условия эксплуатации крана

Рис.2 Общий вид модели крана

BUILDING STRUCTURES, BUILDINGS AND CONSTRUCTIONS

Рис.3. Цветовое обозначение:

красный – уголковый профиль; зелёный – двутавровый; синий и коричневый – тавровый профиль

При таких допущениях достигается некоторый запас прочности. Все расчеты выполнялись для конструкций крана без дефектов (погнутости, трещины, расслоение металла и т.д), не учитывались дефекты в узлах при монтаже крана.

Расчетная схема рассматривалась как система общего вида, деформации которой и ее основные неизвестные представлены линейными перемещениями узловых точек вдоль осей X, Y, Z и поворотами вокруг этих осей (рис.4). На рис. 5–6 приводятся сейсмические нагрузки при расчёте.

Рис.4. Общая расчетная схема

Рис. 5. Задание сейсмического воздействия по X

СТРОИТЕЛЬНЫЕ КОНСТРУКЦИИ, ЗДАНИЯ И СООРУЖЕНИЯ

Рис. 6. Задание сейсмического воздействия по Y

Набор проверок определялся типом поперечного сечения элемента и комплексом действующих на него нагрузок. Проверка осуществлялась по:

прочности стержней при действии продольной силы N;

устойчивости при сжатии в плоскостях XOZ и XOY;

прочности при действии изгибающего момента My или Mz;

прочности при действии поперечной силы Vz или Vy;

прочности при совместном действии N, My и Mz;

устойчивости в плоскости XOZ или XOY при внецентренном сжатии;

устойчивости из плоскости XOZ или XOY при внецентренном сжатии;

устойчивости плоской формы изгиба при действии момента My;

устойчивости при сжатии с двухосным эксцентриситетом ;

чрезмерным деформациям растянутого волокна.

Результаты проверки приведены на рис.7, 8.

Как видим, даже при неблагоприятном сочетании сейсмических воздействий кран К-651 имеет требуемые прочность и устойчивость и может эксплуатироваться без опасности обрушения. Это позволяет рекомендовать внесение изменений в паспорт

BUILDING STRUCTURES, BUILDINGS AND CONSTRUCTIONS

крана с возможностью его эксплуатации без штрафных санкций со стороны фискальных органов.

Список литература

1.Арискин, М.В. Анализ причин падения башенного крана на основе построения модели в SCAD 11.5 / М.В. Арискин, И.Н. Гарькин // Фундаментальные исследования. – 2016. – Ч. 2, № 10. – С.243–247.

2.Данилов, А.М. Методологические принципы математического моделирования сложных систем / А.М. Данилов, И.А. Гарькина // Вестник ПГУАС: строительство,

наука, образование. – 2015. – №1. – С.76–79.

3.Гарькина, И.А. Проблема многокритериальности при управлении качеством сложных систем / И.А. Гарькина, А.М. Данилов, В.О. Петренко // Мир транспорта и технологических машин. – 2013. – №2(41). – С.123–129.

References

1.Ariskin, M.V. Analysis of the causes of the fall of the tower crane on the basis of model building in SCAD 11.5 / M.V. Ariskin, I.N. Garkin // Fundamental Research. – 2016. – Part 2, No. 10. – P.243–247.

2.Danilov, A.M. Methodological principles of mathematical modeling of complex systems / A.M. Danilov, I.A. Garkina // Vestnik PGUAS: construction, science, education. – 2015. – №1. – P.76–79.

3.Garkina, I.A. The problem of multicriteria in the management of the quality of complex systems / I.A. Garkina, A.M. Danilov, V.O. Petrenko // The World of Transport and Technological Machines. – 2013. – №2 (41). – P.123–129.

ИНЖЕНЕРНЫЕ СИСТЕМЫ

ИНЖЕНЕРНЫЕ СИСТЕМЫ

ENGINEERING SYSTEMS

УДК 541.135. 5

МОДЕЛИРОВАНИЕ ПРОЦЕССА ГАЗООБРАЗОВАНИЯ ВОДОРОДА

В ПРОТОЧНЫХ ТРЕХМЕРНЫХ ЭЛЕКТРОДАХ ПРИ ИЗВЛЕЧЕНИИ МЕТАЛЛОВ ИЗ РАСТВОРОВ ЭЛЕКТРОЛИТОВ

А. Н. Кошев, В. К. Варенцов

Разработаны математическая модель совместного восстановления ионов металла и водорода в проточном трехмерном электроде с учетом меняющихся характеристик процесса и электрода в течение электролиза, а также математическая модель образования и перемещения газообразного водорода по толщине проточного трехмерного электрода. Экспериментальным и расчетным путем обоснована необходимость учета образования газообразного водорода при математическом моделировании процесса, показано его влияние на электропроводность раствора и эффективность электроосаждения металла. Приведены некоторые результаты численного анализа.

Ключевые слова: математическая модель, дифференциальные уравнения, проточный трехмерный электрод, выделение газообразного водорода, осаждение металла, удельная электропроводность

ENGINEERING SYSTEMS

MODELING THE PROCESS OF GENERATION HYDROGEN IN 3D-POROUS ELECTRODES AT ELECTRODEPOSITION OF METALS

A. N. Koshev, V. K. Varentsov

The article presents a mathematical model for the electrodeposition of the metal and hydrogen in flow-through three-dimensional electrodes, taking into account changes in process parameters and electrode during electrolysis. Developed a mathematical model of the formation and movement of hydrogen gas through the thickness of a flowing three-dimensional electrode. The necessity to take into account the formation of gaseous hydrogen is substantiated, its effect on the electrical conductivity of the solution and the efficiency of the electrodeposition of the metal are shown. Some results of numerical analysis are given.

Keywords: mathematical model, differential equation, three-dimensional flow-through electrode, hydrogen gas, deposition of metals, specific conductance

1. Введение

Результаты теоретических и экспериментальных исследований электроосаждения металлов на проточные трехмерные электроды (ПТЭ) из углеродных волокнистых материалов (УВМ) свидетельствуют о том, что параллельная реакция восстановления ионов водорода 2Н+ + 2e = Н2 существенно влияет на эффективность процесса осаждения металлов, распределение металлов по толщине электрода, ограничивает производительность процесса, увеличивает энергозатраты, влияет на свойства электродного углеродного материала, кинетику электроосаждения металла [1–3].

Восстановление ионов водорода совместно с ионами металла (металлов) оказывает комплексное воздействие на целевую реакцию – восстановление ионов металла вплоть до металлической фазы. Макрокинетика процесса образования газообразного водорода является многостадийной – от присоединения электрона к ионам водорода на поверхности волокон УВМ до вывода образующегося газообразного водорода из объема ПТЭ. Результатов детального, поэтапного рассмотрения влияния этого процесса на электроосаждение металлов на ПТЭ нами в литературе не найдено. Реакция образования газообразного водорода и ее влияние на электропроводность жидкой фазы электрода и электролита и на неизбежно связанное с этим перераспределение поляризации и локальных плотностей тока парциальных реакций по толщине электрода осаждающихся металлов не учитываются в математических моделях электроосаждения металлов в ПТЭ из УВМ [4, 5]. В то же время известно, что соотношение электропроводностей жидкой и твердой фаз ПТЭ существенно влияет на показатели процесса электроосаждения металлов [1, 3, 4, 6].

Очевидно, что при осаждении металла на проточном трехмерном электроде, в том числе из углеродного волокнистого материала, все происходящие процессы необходимо рассматривать в динамике, т.е. от начальной фазы электролиза до осаждения металла и последующего заполнения объема проточного трехмерного электрода металлом. Такие исследования возможны только с использованием методов физикоматематического моделирования, которые позволяют учитывать изменение характеристик процесса электроосаждения металла и выделения водорода, поляризаций, локальных плотностей тока, массы осаждающегося металла, количества (объема) выделившегося водорода, электропроводностей твердой и жидкой фаз ПТЭ в процессе электролиза и таким образом решать задачу по исследованию макрокинетики рассматриваемых процессов.

Эффект выделения водорода на поверхности волокон УВМ в процессе осаждения различных металлов наглядно показан на рис. 1. Приведенные микрофотографии осадков металлов на УВЭ свидетельствуют о том, что доля поверхности, на которой выделяется водород, может быть существенной. Потому рассмотрение вопроса о влиянии реакции восстановления ионов водорода на электроосаждение металлов на ПТЭ является важным и целесообразным.

ИНЖЕНЕРНЫЕ СИСТЕМЫ

Рис. 1. Осадки металлов на нитях УВМ:

А – медь; Б – никель; В – медь; Г – кадмий. (Вспучивание и разрывы в покрытии металлов соответствуют местам на углеграфитовых нитях, где происходит образование газообразного водорода)

В данной работе приводятся математические модели электрохимических процессов в ПТЭ, позволяющие рассчитывать все необходимые электрохимические функции во времени и пространстве, а также процессы образования и перемещения газообразного водорода по толщине проточного трехмерного электрода, его влияние на электропроводность раствора и эффективностьэлектроосажденияметалла.

2. Математическая модель для расчета процессов в ПТЭ

Для расчета распределения электрохимических процессов в проточном трехмерном электроде (ПТЭ) ранее нами были получены математические модели, представленные в работах [7, 8] и описывающие процессы электроосаждения металлов из поликомпонентных систем при нестационарном электролизе, с учетом возможного перераспределения по толщине электрода таких основных параметров процесса и электрода, как электропроводность твердой и жидкой фаз системы, линейная скорость протока электролита, удельная реакционная поверхность электрода и др. В данной работе мы рассмотрим случай, когда электроактивными компонентами процесса являются ионы осаждаемого на ПТЭ металла и водорода, разряжающиеся на углеграфитовых волокнах.

Известно, что в условиях, когда направление протока электролита и линии электрического поля взаимно параллельны, что реализуется в большинстве конструкций электрохимических реакторов с ПТЭ, в том числе из УВМ [3,9,10], правомерно использование одномерных моделей, так как электрохимические процессы в ПТЭ на любой линии 0 x L , где L− толщина электрода, можно считать идентичными, при

единичное сечение электрода, перпендикулярное направлению потока раствора и линиям тока, ассоциируется с точкой, имеющей координату х по толщине электрода.